
Wetenschap
Snelle laseroplosser voor het fase-ophaalprobleem
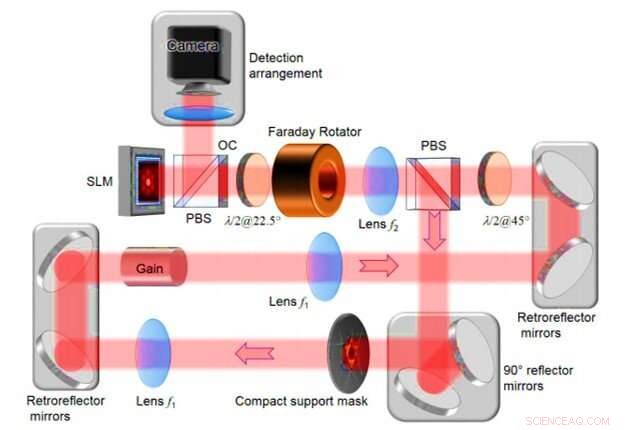
Gedetailleerde experimentele digitale ring gedegenereerde holte laseropstelling. SLM - ruimtelijke lichtmodulator; PBS - polariserende bundelsplitser; λ/2@22,5° - halfgolfplaat bij 22,5° hoekoriëntatie; λ/2@45° - halfgolfplaat in een hoek van 45°; compact steunmasker - opening in de holte in het Fourier-vlak; OC-uitgangskoppeling. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aax4530
Natuurkundigen kunnen op maat gemaakte fysieke systemen verkennen om uitdagende rekentaken snel op te lossen door spinsimulators te ontwikkelen, combinatorische optimalisatie en focussering van licht door verstrooiende media. In een nieuw verslag over wetenschappelijke vooruitgang , C. Tradonsky en een groep onderzoekers van de departementen Natuurkunde in Israël en India hebben het fase-ophaalprobleem aangepakt door een object te reconstrueren op basis van zijn verstrooide intensiteitsverdeling. Het experimentele proces loste een bestaand probleem op in disciplines variërend van röntgenbeeldvorming tot astrofysica die geen technieken hebben om een interessant object te reconstrueren, waar wetenschappers doorgaans indirecte iteratieve algoritmen gebruiken die inherent traag zijn.
In de nieuwe optische benadering Tradonsky et al. gebruikten daarentegen een digitale gedegenereerde holtelaser (DDCL) -modus om het object van belang snel en efficiënt te reconstrueren. De experimentele resultaten suggereerden dat de versterkingsconcurrentie tussen de vele lasermodi fungeerde als een zeer parallelle computer om het fase-ophaalprobleem snel op te lossen. De aanpak is van toepassing op tweedimensionale (2-D) objecten met bekende compacte ondersteuning en objecten met complexe waarden, om beeldvorming te generaliseren via verstrooiingsmedia, terwijl u andere uitdagende rekentaken uitvoert.
Om relatief eenvoudig de intensiteitsverdeling van verstrooid licht van een onbekend object te berekenen, onderzoekers kunnen de bron van de absolute waarde van de Fourier-transformatie van een object berekenen. De reconstructie van een object uit zijn verstrooide intensiteitsverdeling is, echter, slecht gesteld, omdat fase-informatie verloren kan gaan en diverse faseverdelingen in het werk tot verschillende reconstructies kunnen leiden. Wetenschappers moeten daarom vooraf informatie verkrijgen over de vorm van een object, positiviteit, ruimtelijke symmetrie of schaarste voor nauwkeurigere objectreconstructies. Dergelijke voorbeelden zijn te vinden in de astronomie, korte-puls karakteriseringsstudies, Röntgendiffractie, radardetectie, spraakherkenning en bij beeldvorming over troebele media. Tijdens de reconstructie van objecten met een eindige omvang (compacte ondersteuning), onderzoekers bieden een unieke oplossing voor het fase-ophaalprobleem, zolang ze dezelfde verstrooide intensiteit modelleren met een voldoende hogere resolutie.
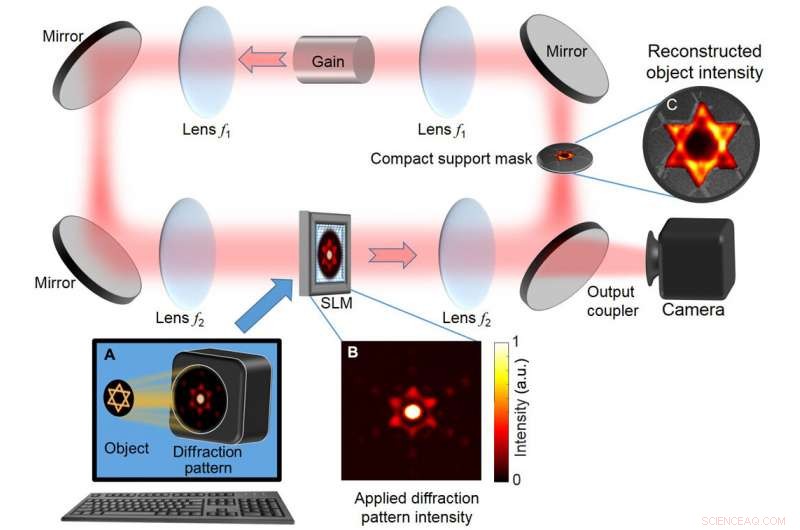
Basis DDCL-arrangement voor het snel ophalen van fasen. (A) Berekende verspreide intensiteitsverdeling van het object (in wezen de Fourier-intensiteitsverdeling) wordt toegepast op een SLM, die is opgenomen in een ringontaarde holtelaser die tot 100 kan ondersteunen, 000 gedegenereerde transversale modi. Een masker in de vorm van de objectgrenzen (compacte ondersteuning) op het Fourier-vlak filtert externe modi uit die niet overeenkomen met de compacte ondersteuning. Met deze laseropstelling het laserproces levert een zelfconsistente oplossing op die voldoet aan zowel de verstrooide intensiteitsverdeling getoond in (B) als de compacte ondersteuningsbeperking. (C) De intensiteit van het gereconstrueerde object verschijnt op het compacte ondersteuningsmasker en wordt afgebeeld op de camera. a.u., willekeurige eenheden. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aax4530
Natuurkundigen hadden de afgelopen tien jaar verschillende algoritmen ontwikkeld om het fase-ophaalprobleem op te lossen, inclusief het Gerchberg-Saxton (GS) foutreductiealgoritme, hybride input-input-algoritme en ontspannen gemiddelde alternerende reflecties (RAAR). Echter, ze zijn gebaseerd op iteratieve projecties die zelfs op krachtige computers relatief traag zijn. Als een alternatief, onderzoeksteams kunnen computationele uitdagingen aangaan met behulp van specifiek op maat gemaakte fysieke systemen. Hoewel dergelijke systemen geen universele Turing-machines zijn (d.w.z. ze kunnen geen willekeurige berekeningen uitvoeren), ze kunnen mogelijk een specifieke klasse van problemen efficiënt oplossen. Het oplossen van moeilijke problemen met dergelijke systemen kan voordelig zijn in vergelijking met het gebruik van conventionele computers.
Tradonsky et al hebben experimenteel een nieuw optisch systeem gedemonstreerd om fase-ophaalproblemen snel op te lossen op basis van een digitale gedegenereerde holtelaser (DDCL). Het apparaat bevatte twee beperkingen, inclusief de Fourier-magnitudes van verstrooid licht van een object en de compacte drager. Het niet-lineaire laserproces in de holte resulteerde in een zelfconsistente oplossing die aan beide beperkingen voldeed. Het onderliggende fysieke mechanisme in de DDCL was vergelijkbaar met dat waargenomen met spinstimulatoren van de optische parametrische oscillator (OPO).
Zowel OPO-simulators als DDCL's hebben optimalisaties uitgevoerd via een extreem snelle werking met de mogelijkheid om lokale minima te vermijden en hadden een niet-Gaussiaans golfpakket. De wetenschappers faciliteerden de compacte ondersteuningsopening in de holte om verschillende configuraties van laserfasen te garanderen om te resulteren in verschillende verliezen, om de configuratie met minimale verliezen in staat te stellen de moduscompetitie te winnen en het faseprobleem op te lossen. Het DDCL-systeem bevatte veel aantrekkelijke en belangrijke functies, waaronder een hoog parallellisme om miljoenen parallelle experimentele realisaties te bieden, korte retourtijden van ongeveer 20 nanoseconden, snelle convergentietijden en een inherente selectiemodus die minimaal verlies veroorzaakte als gevolg van modusconcurrentie. In theorie, van alle in de tijd evoluerende faseconfiguraties, degene met de hoogste energie won de moduscompetitie ten opzichte van de beperkte winst. Als resultaat, groter het aantal initiële onafhankelijke configuraties in de praktijk, hoe groter de kans dat het systeem een juiste oplossing vindt met een stabiele configuratie en zonder verliezen.
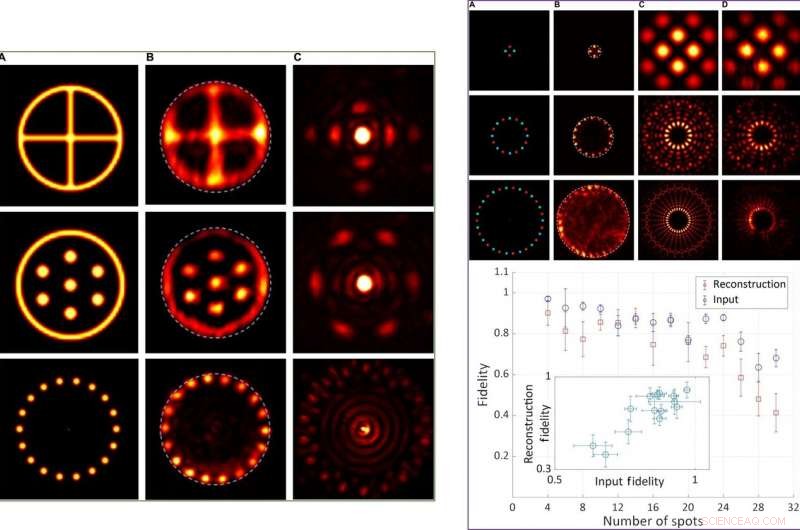
LINKS:Experimentele resultaten voor centrosymmetrische objecten met reële waarde. Kolom (A) Intensiteitsverdelingen van de werkelijke objecten. Kolom (B) Gedetecteerde intensiteitsverdeling van de gereconstrueerde objecten, met behulp van een cirkelvormige opening als compacte ondersteuning. Kolom (C) Fourier-intensiteitsverdelingen bij de SLM. RECHTS:Experimentele en kwantitatieve resultaten voor getrouwheid als functie van objectcomplexiteit. Boven:Representatieve intensiteitsverdelingen van objecten met 4, 16, en 30 plekken. Kolom (A) Intensiteit (helderheid) en fase (tint) verdelingen van de werkelijke objecten. Kolom (B) Gedetecteerde intensiteitsverdeling van de gereconstrueerde objecten, met behulp van een cirkelvormige opening als compacte ondersteuning. Kolom (C) Berekende Fourier-intensiteitsverdelingen toegepast om de SLM te regelen. Kolom (D) Gedetecteerde overeenkomstige Fourier-intensiteitsverdelingen na wijzigingen door SLM-eigenschappen. Onder:Kwantitatieve getrouwheidswaarden van de Fourier-intensiteitsverdelingen (blauw) en de gereconstrueerde objectintensiteitsverdelingen (rood) als functie van het aantal vlekken in het object (4 tot 30). Inzet:getrouwheidswaarden van de gereconstrueerde objectintensiteitsverdelingen als functie van de getrouwheidswaarden van de Fourier-intensiteitsverdelingen voor alle metingen. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aax4530.
In de proefopstelling is Tradonsky et al. omvatten een ring gedegenereerde holtelaser met een inherent versterkingsmedium, twee 4f-telescopen en een amplitude-ruimtelijke lichtmodulator (SLM). Het systeem omvatte ook een opening in de holte, 3D-reflectiespiegels en een uitgangskoppeling. Het team gebruikte de linker 4f-telescopen om het midden van het versterkingsmedium op de SLM af te beelden en controleerde de transmissie bij elke pixel. onafhankelijk. Ze combineerden de opening in de holte met de SLM om de intensiteitsverdeling van de laserstraling te regelen en te vormen. Toen de wetenschappers een opening in de holte (compact ondersteuningsmasker) plaatsten in het Fourier-vlak tussen de twee lenzen, elke faseverdeling vertoonde een ander verliesniveau. Bijgevolg, de faseverdeling met minimaal verlies was de meest waarschijnlijke lasermodus in het onderzoek. Het team overwoog twee verdienste om de kwaliteit van het systeem te kwantificeren, inclusief de betrouwbaarheid van de oplossing en de rekentijd. Het onderzoeksteam verkreeg representatieve resultaten voor centrosymmetrische objecten met een zeer goede overeenkomst tussen intensiteitsverdelingen van het originele (werkelijke object) en gereconstrueerde vormen.
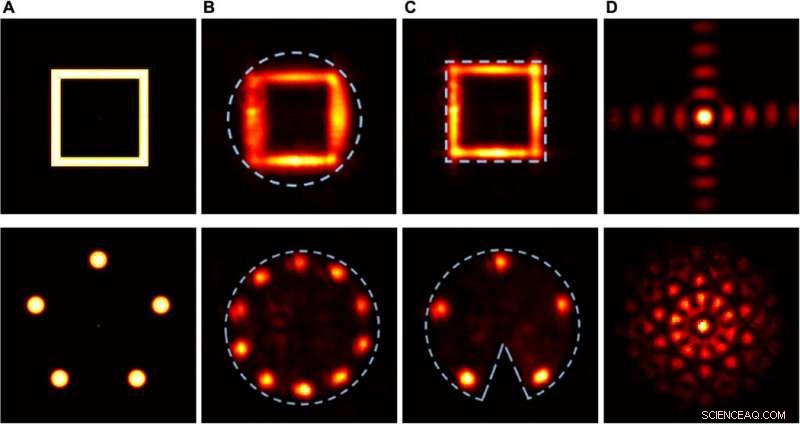
Experimentele resultaten die het kwalitatieve effect van strakheid en asymmetrie van compacte steunen aantonen. Kolom (A) Intensiteitsverdeling van de werkelijke objecten. Kolom (B) Gedetecteerde intensiteitsverdeling van de gereconstrueerde objecten, met behulp van een cirkelvormige opening als compacte ondersteuning. Kolom (C) Gedetecteerde intensiteitsverdeling van de gereconstrueerde objecten, met een vierkante opening als strakke compacte ondersteuning (bovenste rij) en een cirkelvormige opening met een wig als asymmetrische compacte ondersteuning (onderste rij). Kolom (D) Fourier-intensiteitsverdelingen bij de SLM. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aax4530
Tradonsky et al. maten het effect van objectcomplexiteit op de betrouwbaarheid van de reconstructie en vormden representatieve intensiteitsverdelingen voor objecten met vier, 16, en 30 plekken. De resultaten toonden aan dat objecten met een hogere complexiteit (die met meer vlekken) een hogere complexiteit Fourier-intensiteitsverdeling vertoonden, met ingewikkelde details die met het huidige systeem niet konden worden opgelost. Ze merkten ook op dat de invoer- en reconstructiegetrouwheid afneemt met toenemende objectcomplexiteit, die ze toeschreven aan het fluctuerende technische geluid van de laserpomp. Ze voerden kwalitatieve experimenten uit om het effect van strakheid en symmetrie tijdens objectreconstructie te beoordelen. De resultaten toonden aan dat een strakke compacte ondersteuning de kwaliteit van het gereconstrueerde object aanzienlijk verbeterde.
Het team onderzocht vervolgens de kwantitatieve effecten van de straal van de compacte steunopening op de kwaliteit en betrouwbaarheid van de reconstructie. Voor grotere objecten onderging de representatieve intensiteit een snel verval tijdens de getrouwheid van de reconstructie, omdat de laser de objectvorm niet kon ondersteunen. Bij objecten die kleiner zijn dan de compacte steunopening, Tradonsky et al. observeerden een langzamer verval in trouw. In totaal, ze observeerden verminderde reconstructiegetrouwheid wanneer de camera het gemiddelde nam over meerdere realisaties van een object binnen het systeem.
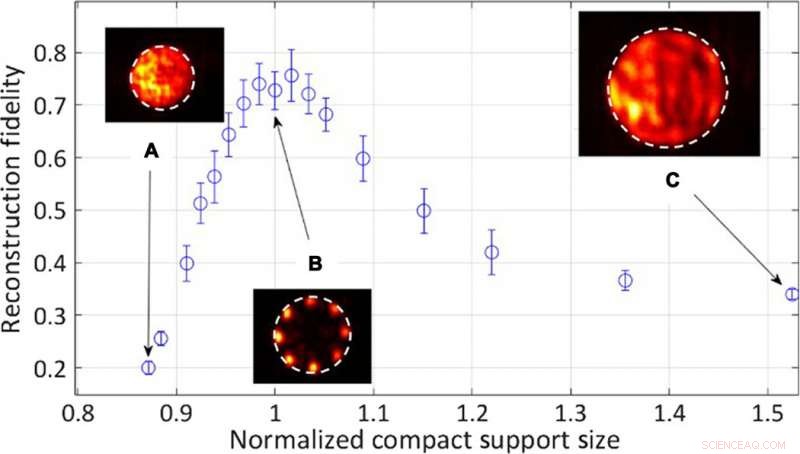
Experimentele kwantitatieve resultaten voor reconstructiegetrouwheid als een functie van de compacte steunstraal van de opening genormaliseerd door de objectgrootte. Insets:typische gereconstrueerde objectintensiteitsverdelingen. (A) Compacte ondersteuningsradius is 87% van de objectradius. (B) Objectstraal is gelijk aan compacte steunstraal. (C) Compacte ondersteuningsradius is 152% van de objectradius. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aax4530.
Over het algemeen, de resolutie van de gereconstrueerde objecten was relatief laag als gevolg van faseafwijkingen in de laserholte. Het team stelde voor om het systeem te optimaliseren en aberraties te verminderen voor een betere resolutie. De wetenschappers analyseerden ook de tijd die nodig was om een reconstructieoplossing aan te bieden met behulp van het systeem en vonden de door de SLM (spatial light modulator) en de camera-uitlezing gedicteerde tijdsduren van ongeveer 20 ms. De werkelijke rekentijd van laseren duurde slechts minder dan 100 nanoseconden. Toen Tradonsky et al. de experimentele opstelling optimaliseerden met behulp van een Q-switched lineaire gedegenereerde holtelaseropstelling met pockelcellen, ze brachten de totale rekentijd van het systeem terug tot ongeveer 100 nanoseconden. Ter vergelijking, de reconstructietijd met het RAAR-algoritme duurde één seconde.
Op deze manier. C. Tradonsky en collega's presenteerden een optisch systeem voor het snel ophalen van fasen met behulp van een nieuwe DDCL (digitale gedegenereerde holtelaser). De rekentijd bedroeg 100 nanoseconden; ordes van grootte sneller dan conventionele, op algoritmen gebaseerde rekensystemen. Op basis van de resultaten, verschillende aanpassingen aan het DDCL-systeem kunnen mogelijk de prestaties verbeteren, inclusief een grotere lengte van de laserholte om het aantal onafhankelijke parallelle onderzoeken te vergroten. Het onderzoeksteam zal het systeem verder onderzoeken om een verscheidenheid aan problemen op te lossen en de beeldkwaliteit op te lossen na vermeerdering door verstrooiende media.
© 2019 Wetenschap X Netwerk
 Welke effecten hebben chloorfluorkoolstoffen op mensen?
Welke effecten hebben chloorfluorkoolstoffen op mensen?  De sluiting bracht blauwere luchten maar meer nachtelijke ozon naar Californië
De sluiting bracht blauwere luchten maar meer nachtelijke ozon naar Californië Eerste kwantificeerbare waarneming van cloud seeding
Eerste kwantificeerbare waarneming van cloud seeding Er sterven meer mensen in de winter dan in de zomer, maar klimaatverandering kan dit omgekeerd zien
Er sterven meer mensen in de winter dan in de zomer, maar klimaatverandering kan dit omgekeerd zien Chemische waterverontreiniging veroorzaakt door dagelijkse wasmiddelen
Chemische waterverontreiniging veroorzaakt door dagelijkse wasmiddelen
Hoofdlijnen
- Daling van huismus in verband met luchtvervuiling en slechte voeding
- Wat is de formule voor cellulaire ademhaling?
- Diversiteit en immigratie verhogen de productiviteit in microbiële gemeenschappen
- Technologie verhoogt melkgift met 9 procent
- Een plantencelmodel maken met een schoenendoos
- Twee zeldzame aanvallen van zeeleeuwen sluiten baai in San Francisco Bay af
- Wat doet veel van de activiteiten van een cel?
- Het verlichten van sojabladeren kan de voedselvoorziening stimuleren
- Het belang van DNA-moleculen
- De voordelen van MOSFET boven BJT

- Een nieuwe strategie om een high-fidelity mixed-species verstrengelingspoort te implementeren

- Intelligente regeling van modus-vergrendelde femtoseconde-pulsen door spectrale analyse met time-stretch-ondersteuning
- Natuurkundigen stellen nieuwe theorieën voor over zwarte gaten uit het zeer vroege heelal

- Adiabatische snelkoppelingen:kort en krachtig in de kwantumwereld

 Waarom woorden taal maken
Waarom woorden taal maken Ideeën voor Science Fair-projecten op vis
Ideeën voor Science Fair-projecten op vis  Wetenschappers onderzoeken de effecten van zwarte koolstof op het klimaat in het noordpoolgebied tijdens de winter en de lente
Wetenschappers onderzoeken de effecten van zwarte koolstof op het klimaat in het noordpoolgebied tijdens de winter en de lente Kleine verbindingen voor herconfigureerbare microstructuren
Kleine verbindingen voor herconfigureerbare microstructuren Hoe HP naar Amps & Volts wordt geconverteerd
Hoe HP naar Amps & Volts wordt geconverteerd  Begrafenispraktijken wijzen op een onderling verbonden vroegmiddeleeuws Europa
Begrafenispraktijken wijzen op een onderling verbonden vroegmiddeleeuws Europa X- en Y-onderscheppingen zoeken op een grafische rekenmachine
X- en Y-onderscheppingen zoeken op een grafische rekenmachine  Klein, nauwkeurige en betaalbare gyroscoop voor navigeren zonder GPS
Klein, nauwkeurige en betaalbare gyroscoop voor navigeren zonder GPS
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

