
Wetenschap
De klassieke elegantie van tijdkristallen waarderen
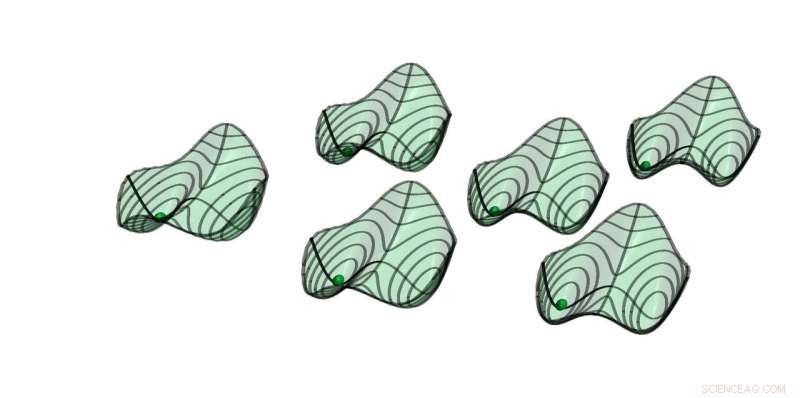
Quasi-potentialen van zes parametrische oscillatoren met zwakke alles-naar-alles-koppeling. Stabiele oplossingen bevinden zich op de minima. De bolletjes geven de symmetrische oplossing aan, waar alle oscillatoren in fase zijn. (Screenshot van begeleidende animatie) Credit:ETH Zürich/D-PHYS Toni Heugel
Structuren die bekend staan als tijdkristallen, die zich herhalen in de tijd zoals conventionele kristallen zich herhalen in de ruimte, hebben onlangs de interesse en verbeeldingskracht van onderzoekers in verschillende disciplines gewekt. Het concept is voortgekomen uit de context van quantum veellichamensystemen, maar ETH-natuurkundigen hebben nu een veelzijdig raamwerk ontwikkeld dat verbanden met klassieke werken van bijna twee eeuwen verduidelijkt, daarmee een verenigend platform biedend om schijnbaar ongelijksoortige verschijnselen te verkennen.
In een kristal, atomen zijn sterk geordend, goed gedefinieerde locaties bezetten die ruimtelijke patronen vormen. Zeven jaar geleden, de Nobelprijswinnaar voor natuurkunde van 2004, Frank Wilczek, dacht na over de mogelijkheid van een tijdanaloog van kristallijne ruimtelijke ordening - systemen die aanhoudende periodieke temporele modulaties vertonen in hun laagste energietoestand. Het concept van dergelijke structuren met een oscillerende grondtoestand is zeer intrigerend. Helaas, niet lang nadat het idee werd gepubliceerd, het is bewezen dat zulke tijdkristallen niet mogelijk zijn zonder fundamentele natuurwetten te overtreden. Echter, daaropvolgend theoriewerk suggereerde dat wanneer kwantum veel-lichamensystemen periodiek worden aangestuurd, nieuwe aanhoudende tijdcorrelaties ontstaan die doen denken aan de tijdkristallen van Wilczek. Deze aangedreven systemen werden discrete tijdkristallen genoemd, en anno 2017, de eerste experimentele realisaties van dergelijke toestanden werden gerapporteerd in ensembles van gekoppelde deeltjes (ionen, elektronen en kernen) die kwantummechanische eigenschappen vertonen.
Een niet zo korte geschiedenis van tijdkristallen
Het duurde niet lang, scherpzinnige waarnemers zagen duidelijke overeenkomsten tussen discrete tijdkristallen in kwantumsystemen en zogenaamde parametrische resonatoren, een concept in de klassieke natuurkunde dat in 1831 door Michael Faraday terugkwam op het werk. Het verband tussen deze twee oeuvre bleef bestaan, echter, ondoorzichtig. Nutsvoorzieningen, theoretici hebben een nieuw raamwerk ontwikkeld dat een lange weg gaat in de richting van het opheffen van de dubbelzinnigheden rond de overeenkomsten tussen periodiek aangedreven klassieke en kwantumsystemen.
Schrijven in een artikel dat vandaag in het tijdschrift is gepubliceerd Fysieke beoordelingsbrieven , Toni Heugel, een doctoraat student in de afdeling Natuurkunde aan de ETH Zürich, en Matthias Oscity, een student aan dezelfde instelling, in samenwerking met Dr. Ramasubramanian Chitra en Prof. Oded Zilberberg van het Instituut voor Theoretische Fysica en met Dr. Alexander Eichler van het Laboratorium voor Vaste-stoffysica, rapporteer theoretisch en experimenteel werk dat vaststelt hoe discrete tijdkristallen kunnen worden gegenereerd die, aan de ene kant, vereisen geen kwantummechanische effecten en, anderzijds, echte veellichameneffecten vertonen, wat een kenmerk is van discrete tijdkristallen die worden gerapporteerd in kwantumsystemen.
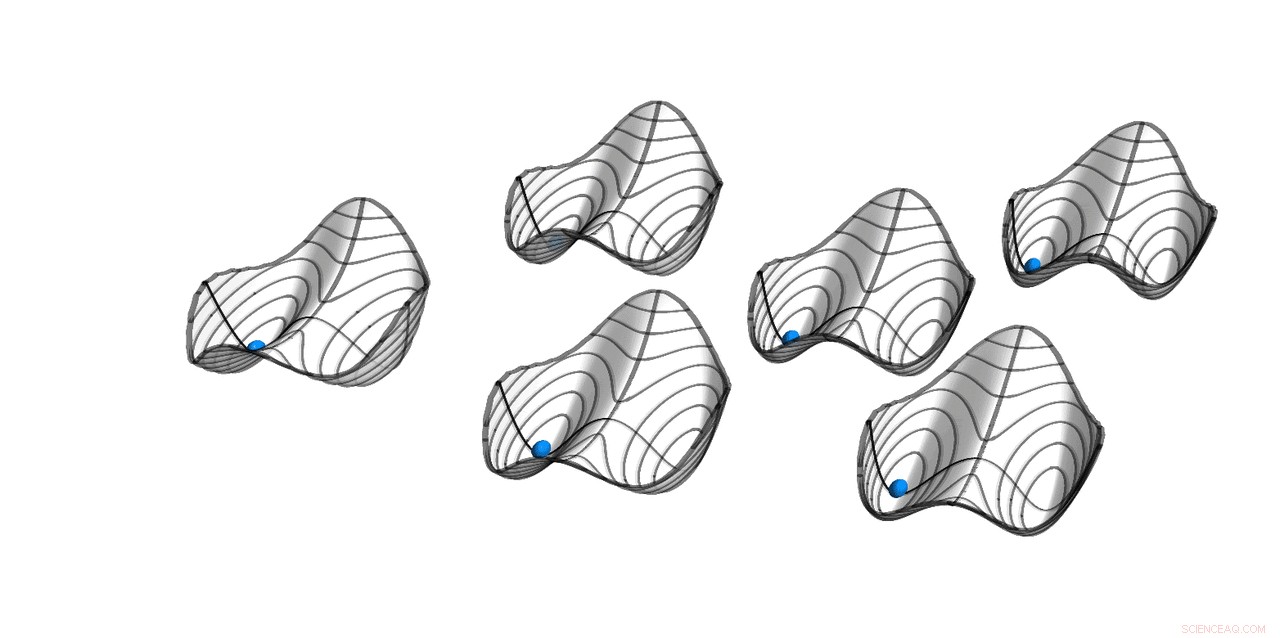
Quasi-potentialen van zes parametrische oscillatoren met zwakke alles-naar-alles-koppeling. Stabiele oplossingen bevinden zich op de minima. De bolletjes geven de symmetrische oplossing aan, waarbij alle oscillatoren in fase zijn. De Hamiltoniaan H bepaalt de beweging van het systeem heeft periode T, terwijl de oplossing zelf periode 2T heeft. Deze discrete tijdtranslatie symmetrie breken maakt het systeem een discrete tijdkristal. Krediet:ETH Zürich/D-PHYS Toni Heugel
Vele manieren om subharmonische frequenties te krijgen
Er is één duidelijke overeenkomst tussen klassieke parametrische resonatoren en experimenteel gerealiseerde discrete tijdkristallen in quantum veellichamensystemen:beide vertonen opkomende dynamiek bij frequenties die fracties zijn van de aandrijffrequentie. In de context van discrete tijdkristallen, de opkomst van oscillaties bij dergelijke subharmonische frequenties breekt de temporele periodiciteit van het aangedreven systeem, het verstrekken van een 'tijd analoog' aan kristallijne ruimtelijke orde, waarin de symmetrie van de ruimte wordt verbroken. In klassieke parametrisch gestuurde systemen, subharmonische frequenties verschijnen op meer bekende manieren:een kind op een schommel, bijvoorbeeld, wijzigt het zwaartepunt met tweemaal de frequentie van de resulterende oscillatie, of de paardenstaart van een hardloper oscilleert met de helft van de frequentie van de verticale hoofdbeweging.
Maar hebben deze verschillende verschijnselen iets met elkaar te maken? Ja, zeggen de ETH-fysici. Vooral, ze lokaliseren waar veel-lichaamsaspecten verschijnen in klassieke systemen. Om dit te doen, ze beschouwden klassieke niet-lineaire oscillatoren met een afstembare koppeling ertussen.
Verbindend raamwerk voor periodiek aangedreven klassieke en kwantumsystemen
Het is algemeen bekend dat voor bepaalde aandrijffrequenties en sterktes, parametrische oscillatoren worden onstabiel en ondergaan dan een zogenaamde periodeverdubbelende bifurcatie, waarboven ze oscilleren op de helft van hun aandrijffrequentie. Heugel, Oscity en hun collega's onderzoeken wat er gebeurt als verschillende van dergelijke oscillatoren aan elkaar worden gekoppeld. Zowel in berekeningen als in experimenten met twee strings met variabele koppeling daartussen, ze vinden twee verschillende regimes. Als de koppeling sterk is, het tweesnarige systeem beweegt samen, in wezen de bewegingen van het kind op een schommel of de paardenstaart van een hardloper nabootsen. Echter, in het geval van een zwakke koppeling tussen de snaren, de dynamiek van elke snaar is vergelijkbaar met die weergegeven door het ontkoppelde systeem. Als gevolg hiervan, de gekoppelde oscillatoren splitsen niet collectief maar splitsen individueel op bij enigszins verschillende parameters van de aandrijving, wat leidt tot een rijkere algemene dynamiek, die steeds complexer worden naarmate de systemen groter worden.
De ETH-onderzoekers stellen dat dergelijke zwak gekoppelde modi vergelijkbaar zijn met de modi die voorkomen in kwantumsystemen met veel lichamen, wat impliceert dat hun raamwerk het gedrag dat experimenteel in deze systemen wordt waargenomen, zou kunnen verklaren. Bovendien, het nieuwe werk schrijft algemene voorwaarden voor het genereren van klassieke veeldeeltjestijdkristallen. Deze zouden uiteindelijk kunnen worden gebruikt om zowel de kenmerken van hun kwantumtegenhangers te interpreteren als te onderzoeken.
Bij elkaar genomen, deze bevindingen bieden daarom een krachtig verenigend raamwerk voor periodiek aangedreven klassieke en kwantumsystemen die dynamiek vertonen bij opkomende subharmonische frequenties - systemen die tot nu toe in zeer verschillende contexten zijn beschreven, maar misschien toch niet zo verschillend.
Hoofdlijnen
- Wat is de structuur van stamcellen?
- Wat is de Chromatins-functie?
- Plantencellen overleven maar stoppen met delen bij DNA-schade
- Epitheliale cellen: definitie, functie, typen en voorbeelden
- Wat maakt mensen gelukkiger -- objecten of ervaringen?
- Een natuurlijke schimmelstam kan olielekkages opruimen en de oliezanden van Albertas weer tot leven brengen
- Wat zijn de vier stikstofbasen van DNA?
- Wat zijn de voordelen van Ribosomes?
- Hoe maak je een Paper Mache Cell
- Team ontwikkelt nieuwe wiskundige vergelijking om cavitatie te voorspellen

- Machinaal lerende modellen van materie voorbij interatomaire potentialen

- Dekentje licht geeft mogelijk betere kwantumcomputers

- Natuurkunde kan snellere oplossingen bieden voor lastige rekenproblemen

- PPPL-fysici bouwen diagnose die de plasmasnelheid in realtime meet

 Koolteerkit belangrijke bron van PAK-verontreiniging in zijrivieren van de Grote Meren
Koolteerkit belangrijke bron van PAK-verontreiniging in zijrivieren van de Grote Meren Toenemend Arctisch zoetwater wordt aangedreven door klimaatverandering
Toenemend Arctisch zoetwater wordt aangedreven door klimaatverandering Wereldnaties die de armsten in de steek laten op het gebied van energiedoelen:studie
Wereldnaties die de armsten in de steek laten op het gebied van energiedoelen:studie Economische synthese van polyacrylaten en polymethacrylaten uit biobased materialen
Economische synthese van polyacrylaten en polymethacrylaten uit biobased materialen Nanolinten op atomaire schaal maken
Nanolinten op atomaire schaal maken Hoogste efficiëntie van flexibele CZTSSe-dunnefilmzonnecel bereikt
Hoogste efficiëntie van flexibele CZTSSe-dunnefilmzonnecel bereikt Oproep om een welzijnsindex toe te voegen aan nationale economische maatregelen
Oproep om een welzijnsindex toe te voegen aan nationale economische maatregelen Micro-dispenser voor langdurige opslag en gecontroleerde afgifte van vloeistoffen
Micro-dispenser voor langdurige opslag en gecontroleerde afgifte van vloeistoffen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


