
Wetenschap
Een sprong in het continuüm
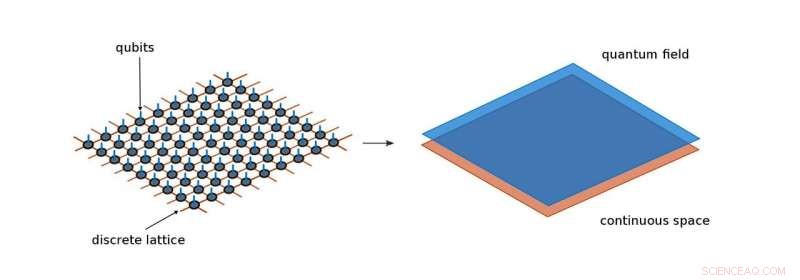
Standaard tensornetwerktoestanden beschrijven kwantumsystemen die op een discrete ruimte leven, of rooster, bijvoorbeeld een array van qubits. Continue tensornetwerken, anderzijds, verklein de roosterafstanden tot ze oneindig klein zijn en herstel zo de continuïteit van de ruimte. Op deze manier, ze kunnen directer omgaan met kwantumvelden. Krediet:Max Planck Instituut voor Quantum Optica
Het nauwkeurig berekenen van de dynamiek van veel op elkaar inwerkende kwantumdeeltjes is een ontmoedigende taak. Er is echter een veelbelovende rekenmethode voor dergelijke systemen:tensornetwerken, die worden onderzocht in de theorieafdeling van het Max Planck Institute of Quantum Optics. De initiële focus van het tensornetwerk was op kwantumdeeltjes beperkt tot een rooster, net zoals ze bijvoorbeeld in kristallen voorkomen, of in de kwantumregisters van toekomstige kwantumcomputers. In een nieuwe krant de postdoctoraal onderzoeker Antoine Tilloy en de theoriedivisiedirecteur Ignacio Cirac slaagden erin om deze benadering uit te breiden naar het continuüm. Een doel op de lange termijn is een elegante rekenmethode voor de kwantumveldentheorieën die de basiskrachten van de natuurkunde beschrijven.
Het beschrijven van de systemen waarin veel kwantumdeeltjes op elkaar inwerken en gezamenlijk nieuwe fenomenen produceren, is een van de fundamentele uitdagingen van de natuurkunde. Een voorbeeld van zo'n quantum veel-lichaamsfenomeen is supergeleiding. De moeilijkheid bij de hand is dat de deeltjes elkaar beïnvloeden. Als resultaat, de kwantummechanische vergelijkingen die dit collectieve gedrag beschrijven, kunnen worden afgeleid, maar niet precies opgelost.
In de kwantummechanica, de dynamische vergelijking moet alle mogelijke toestanden bevatten waarin het systeem zich mogelijk kan bevinden. En dat kunnen er veel zijn. Een voorbeeld dat momenteel populair is in de natuurkunde zijn kwantumbits. Ze worden bijvoorbeeld verkregen uit speciaal geprepareerde elektronen of elektrisch geladen atomen. Dergelijke qubits hebben twee tegengestelde toestanden, die de waarden nul en één kan aannemen. Maar in tegenstelling tot een "klassiek" bit, de qubit kan zich ook in elke superpositie van die twee toestanden bevinden. Als men nu twee qubits koppelt met een zogenaamde kwantumpoort, de abstracte wiskundige ruimte van alle mogelijke kwantumtoestanden verdubbelt. En elke extra qubit verdubbelt het weer. Processoren en datageheugens van conventionele computers worden letterlijk overspoeld door dit exponentieel groeiende aantal mogelijke kwantumtoestanden. Zelfs supercomputers vallen uit na meer dan enkele tientallen qubits. Alleen kwantumcomputers, gehoorzamen aan de regels van de kwantummechanica zelf, ooit zal kunnen omgaan met de dynamiek van grotere kwantumsystemen.
Het onberekenbare berekenbaar maken
Het voorbeeld van de qubits past, omdat Ignacio Cirac en zijn collega's tot de pioniers behoren van dit opkomende gebied van kwantuminformatietechnologie. De methode van "tensornetwerken, " waarover dit artikel gaat, komt ook uit dit onderzoeksgebied. Het maakt het mogelijk om de gigantische ruimte van alle mogelijke kwantumtoestanden van een systeem met meerdere deeltjes op een slimme manier te verkleinen tot een berekenbare grootte. "Stel je alle mogelijke kwantumtoestanden van een veeldeeltjessysteem voor als een enorm cirkelvormig gebied, " legt Antoine Tilloy uit. "Maar de toestanden die echt relevant zijn voor ons systeem passen in een veel kleinere cirkel." De kunst is nu om deze kleine cirkel te vinden in een abstracte wiskundige ruimte, en dat is wat tensornetwerken kunnen doen.
Tilloy is een postdoctoraal onderzoeker in de groep van Cirac en samen hebben ze zojuist een artikel over tensornetwerken gepubliceerd in het tijdschrift Fysieke beoordeling X . Oorspronkelijk, de natuurkundigen pasten ze toe op arrays van individuele qubits. Tensornetwerken vertrouwden dus aanvankelijk op een raster van abstracte wiskundige objecten - een beetje zoals een wiskundige parelsnoer, leven op discrete posities.
Tensornetwerken bleken een succesvol hulpmiddel te zijn om berekeningen uit te voeren voor een grote klasse kwantumsystemen die beperkt waren tot rasters. Dit succes bracht theoretische onderzoeksgroepen wereldwijd op een idee:kan deze methode ook worden toegepast op fysieke systemen die niet op grids leven, maar eerder in continuümruimte? Kortom, het antwoord is ja. In feite, de methode van tensornetwerken kan worden uitgebreid tot het continuüm en dit is wat Tilloy en Cirac in hun nieuwe werk hebben aangetoond.
Nieuwe tool voor kwantumveldentheorieën
Zogenaamde kwantumveldentheorieën zouden een belangrijk toepassingsgebied kunnen zijn voor deze nieuwe toolbox. Deze theorieën vormen de basis van het huidige fysieke wereldbeeld. Ze beschrijven nauwkeurig hoe drie van de vier basiskrachten van de natuurkunde functioneren volgens de kwantummechanica. Deze krachten worden gemedieerd door virtuele deeltjes die slechts bestaan voor de korte tijd die nodig is om hun kracht over te brengen.
In de elektrische kracht, bijvoorbeeld, de mediërende deeltjes zijn virtuele lichtquanta. "Dit valt onder wat bekend staat als kwantumelektrodynamica en is goed begrepen, ", zegt Tilloy. "Het wordt ingewikkelder met wat bekend staat als kwantumchromodynamica." QCD, zoals het kort wordt genoemd, beschrijft de krachten tussen de quarks, die op hun beurt de bouwstenen vormen van de atoomkernen, de protonen en neutronen. gluonen, "klevende deeltjes, " bemiddelt de sterkste kracht in de natuurkunde. En dit "lijmt" de quarks aan elkaar.
Maar in tegenstelling tot de virtuele fotonen, de gluonen kunnen elkaar ook sterk beïnvloeden. Deze "zelfinteractie" leidt tot het onaangename feit dat de vergelijkingen van QCD alleen kunnen worden opgelost in grensgevallen, bij zeer hoge energie. Voor lagere energieën - de normale toestand van materie in onze omgeving - is dit niet mogelijk. Om deze reden, tot nu toe moeten natuurkundigen werken met benaderende oplossingen. De standaardstap hier is om het continuüm op te splitsen in een kunstmatig raster van punten waarvoor een krachtige computer vervolgens benaderende oplossingen kan berekenen.
"Deze stap van discretisatie is complex, ", zegt Tilloy. Bovendien, dergelijke vereenvoudigingen hebben altijd het nadeel dat ze een fundamentele symmetrie van de natuur doorbreken bij het verdelen van het continuüm in een raster van discrete punten. Ze worden dus gedwongen om afstand te nemen van de eigenlijke fysica. De methode van continue tensornetwerken kan hierbij helpen, omdat het deze voorafgaande discretisatie van de ruimte niet vereist. Misschien zal ooit het gedrag van quarks en gluonen bij lage energieën worden begrepen. Vandaag is het nog steeds een open probleem, maar de recent ontdekte continue tensornetwerken kunnen al een deel van de oplossing zijn.
 Brandstofaërosolen die de vervuiling van het milieu verminderen
Brandstofaërosolen die de vervuiling van het milieu verminderen Onderzoekers bevorderen stamceltherapie met biologisch afbreekbare steiger
Onderzoekers bevorderen stamceltherapie met biologisch afbreekbare steiger Nieuwe methode kan scheuren in metaal opsporen lang voordat ze catastrofes veroorzaken
Nieuwe methode kan scheuren in metaal opsporen lang voordat ze catastrofes veroorzaken Nieuwe methode helpt orthotope beeldvorming van hersentumoren duidelijker en sneller te maken
Nieuwe methode helpt orthotope beeldvorming van hersentumoren duidelijker en sneller te maken Mengoplossingen in de kleinste reageerbuisjes ter wereld
Mengoplossingen in de kleinste reageerbuisjes ter wereld
Hoofdlijnen
- Hoe zijn cellen, weefsels en organen aan elkaar gerelateerd?
- Maki's zijn raar omdat het fruit van Madagascar raar is
- Science Fair Project Ideas: Equine
- Hoe maak je een glad endoplasmatisch reticulum uit klei
- Zooplankton Vs. fytoplankton
- Waarom heeft een regenworm een gesloten bloedsomloop?
- De rol van de longen
- De zoektocht naar de zuidelijke rubberboa
- Heb je testangst? Hier is hoe we het moeten aanpakken
- Natuurkunde onderzoeken die verder gaat dan het standaardmodel met het ATLAS-experiment
- Verrassende overeenkomst tussen gestreepte zwarte gaten en supergeleiders bij hoge temperaturen

- Nanodeeltjesinkt produceert gloeiende hologrammen met een eenvoudige inkjetprinter

- Unieke microscoop zorgt voor doorbraak in de kwantumwetenschap

- Ontdek de geheimen van enkele van 's werelds eerste kleurenfoto's

 Kunnen aardbevingssnelheden van magnitude 4 worden gebruikt om grote aardbevingen te voorspellen?
Kunnen aardbevingssnelheden van magnitude 4 worden gebruikt om grote aardbevingen te voorspellen? Hoe werkt chloor om zwembaden schoon te maken?
Hoe werkt chloor om zwembaden schoon te maken?  Leraar schoolbordcomputer is internationale conferentiester
Leraar schoolbordcomputer is internationale conferentiester Manipuleren van ketenlopen in olefinen met behulp van aarde-overvloedige op ijzer gebaseerde katalysatoren
Manipuleren van ketenlopen in olefinen met behulp van aarde-overvloedige op ijzer gebaseerde katalysatoren De declinatie van de zon berekenen
De declinatie van de zon berekenen Nanobuistechnologie leidt tot snelle, goedkope medische diagnostiek
Nanobuistechnologie leidt tot snelle, goedkope medische diagnostiek Koolstof opgelost in Arctische rivieren heeft invloed op onze wereld - zo bestudeer je het
Koolstof opgelost in Arctische rivieren heeft invloed op onze wereld - zo bestudeer je het Gevangenisstraffen voor Franse oplichters in koolstofhandel
Gevangenisstraffen voor Franse oplichters in koolstofhandel
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | French |

-
Wetenschap © https://nl.scienceaq.com

