
Wetenschap
Nieuw dynamisch afhankelijkheidskader kan leiden tot betere neurale sociale en technische systeemmodellen
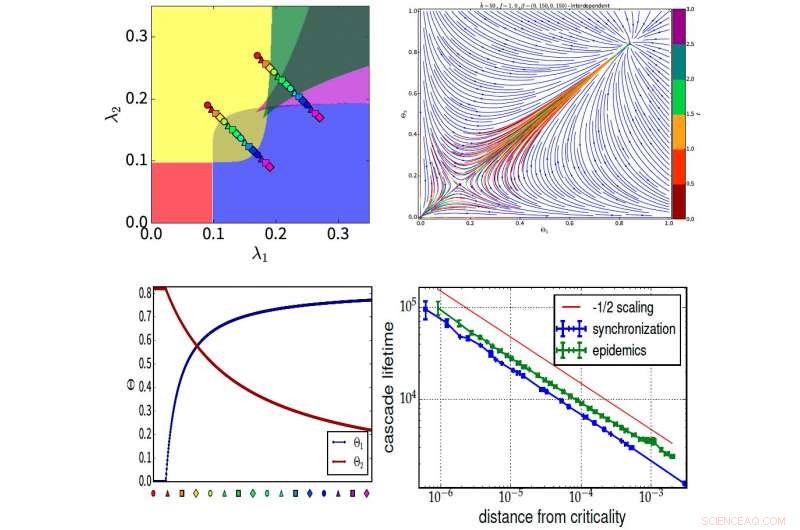
In een onlangs gepubliceerd artikel in Natuurfysica , Bar-Ilan Universiteit Prof. Havlin, en een team van onderzoekers, waaronder Stefano Boccaletti, Ivan Bonamassa, en Michael M. Danziger, een dynamisch afhankelijkheidskader presenteren dat onderling afhankelijke en competitieve interacties tussen dynamische systemen kan vastleggen die worden gebruikt om synchronisatie- en verspreidingsprocessen in meerlaagse netwerken met op elkaar inwerkende lagen te bestuderen. Belangrijkste resultaten in deze afbeelding. (Linksboven) Fasediagram voor twee gedeeltelijk concurrerende Kuramoto-modellen met regio's van multistabiliteit. (Rechtsboven) Theoretische en numerieke resultaten voor het verloop van onderling afhankelijke SIS-epidemieën (Erdos-Renyi-grafieken, gemiddelde graad
Veel complexe systemen in de echte wereld bevatten macroscopische subsystemen die elkaar beïnvloeden. Dit ontstaat, bijvoorbeeld, in concurrerende of elkaar versterkende neurale populaties in de hersenen, het verspreiden van de dynamiek van virussen, en elders. Het is daarom belangrijk om te begrijpen hoe verschillende soorten interacties tussen systemen het algemene collectieve gedrag kunnen beïnvloeden.
In 2010 werd aanzienlijke vooruitgang geboekt toen de theorie van percolatie op onderling afhankelijke netwerken werd geïntroduceerd door Prof. Shlomo Havlin en een team van onderzoekers van de afdeling Natuurkunde van de Bar-Ilan University in een studie gepubliceerd in Natuur . Dit model toonde aan dat wanneer knooppunten in het ene netwerk afhankelijk zijn van knooppunten in een ander om te functioneren, catastrofale cascades van mislukkingen en abrupte structurele overgangen ontstaan, zoals werd waargenomen bij de stroomuitval die in 2003 een groot deel van Italië trof.
Onderling afhankelijke percolatie, echter, is beperkt tot systemen waar functionaliteit uitsluitend wordt bepaald door connectiviteit, dus slechts een gedeeltelijk begrip van een schat aan real-world systemen waarvan de functionaliteit is gedefinieerd volgens dynamische regels.
Onderzoek heeft aangetoond dat twee fundamentele manieren waarop knooppunten in het ene systeem knooppunten in een ander kunnen beïnvloeden, onderlinge afhankelijkheid (of samenwerking), zoals in kritieke infrastructuren of financiële netwerken, en antagonisme (of competitie), zoals waargenomen in ecologische systemen, sociale netwerken, of in het menselijk brein. Onderling afhankelijke en competitieve interacties kunnen ook gelijktijdig plaatsvinden, zoals waargenomen in roofdier-prooirelaties in ecologische systemen, en in binoculaire rivaliteit in de hersenen.
In een onlangs gepubliceerd artikel in Natuurfysica , Bar-Ilan Universiteit Prof. Havlin, en een team van onderzoekers, waaronder Stefano Boccaletti, Ivan Bonamassa, en Michael M. Danziger, een dynamisch afhankelijkheidskader presenteren dat onderling afhankelijke en competitieve interacties tussen dynamische systemen kan vastleggen die worden gebruikt om synchronisatie- en verspreidingsprocessen in meerlaagse netwerken met op elkaar inwerkende lagen te bestuderen.
"Dit dynamische afhankelijkheidskader biedt een krachtig hulpmiddel om veel van de op elkaar inwerkende complexe systemen die ons omringen beter te begrijpen, " schreef Havlin en team. "De veralgemening van afhankelijke interacties van percolatie naar dynamische systemen zorgt voor de ontwikkeling van nieuwe modellen voor neurale, sociale en technologische systemen die de subtiele manieren waarop verschillende systemen elkaar kunnen beïnvloeden beter weergeven."
Het onderzoek van prof. Havlin sinds 2000 heeft baanbrekende nieuwe wiskundige methoden in netwerkwetenschap opgeleverd die hebben geleid tot uitgebreid interdisciplinair onderzoek in het veld. Na de publicatie van de theorie van percolatie door Havlin en zijn collega's, hij ontving de Lilienfeld Prize van de American Physical Society, die wordt toegekend voor "een meest opmerkelijke bijdrage aan de natuurkunde". Eerder dit jaar ontving hij de Israel Prize in Chemistry and Physics.
 Onderzoekers beschouwen de complexiteit van het bioprinten van meercellige weefsels
Onderzoekers beschouwen de complexiteit van het bioprinten van meercellige weefsels Onderzoekers creëren snelkoppeling naar terpeenbiosynthese in E. coli
Onderzoekers creëren snelkoppeling naar terpeenbiosynthese in E. coli Runderembryo regenereert placenta-vormende cellen volledig
Runderembryo regenereert placenta-vormende cellen volledig Chemische reacties die Light
Chemische reacties die Light Nieuwe tool haalt ongrijpbare COVID-19-marker uit menselijk bloed
Nieuwe tool haalt ongrijpbare COVID-19-marker uit menselijk bloed
 Wat met roet bedekt, Honderd jaar oude vogels kunnen ons vertellen over het redden van het milieu
Wat met roet bedekt, Honderd jaar oude vogels kunnen ons vertellen over het redden van het milieu IPCC-rapport schetst catastrofaal beeld van smeltend ijs en stijgende zeespiegel - en de realiteit kan nog erger zijn
IPCC-rapport schetst catastrofaal beeld van smeltend ijs en stijgende zeespiegel - en de realiteit kan nog erger zijn Zeespiegelstijging gekoppeld aan hogere grondwaterstanden langs de kust van Californië
Zeespiegelstijging gekoppeld aan hogere grondwaterstanden langs de kust van Californië NASA kijkt naar compacte tropische storm Don in infrarood licht
NASA kijkt naar compacte tropische storm Don in infrarood licht NASA ziet tropische depressie Khanun sissiperen in Golf van Tonkin
NASA ziet tropische depressie Khanun sissiperen in Golf van Tonkin
Hoofdlijnen
- Hoe huilen werkt
- Studie onthult verschillen in belangrijke evoluties van het genoom van gewassen
- Uit een grootschalig onderzoek blijkt dat veel geplande wegen in de tropen niet gebouwd mogen worden
- Welk vierkant is groter? Honingbijen zien visuele illusies zoals mensen dat doen
- Welk percentage botten in het lichaam bestaat uit het axiale skelet?
- Hoe beschadigt UV-licht de DNA-streng?
- Welk deel van het lichaam maakt bloed?
- Een model van een plantencel in een plastic zak maken
- Waarom hebben zoveel van onze huisdieren overgewicht?
- Hoe werkt Sonication?
- Het ondergrondse ballet van ALICE

- Kwantumsimulatoren voor ijktheorieën

- Nieuwe PPPL-uitvinding zou de efficiëntie van auto- en vrachtwagenmotoren kunnen verbeteren en tegelijkertijd verontreinigende stoffen kunnen verminderen

- De invloed van een magnetisch veld op chirale magnetische correlaties
 Een mogelijke verklaring waarom er geen zwarte gaten van gemiddelde grootte zijn gevonden
Een mogelijke verklaring waarom er geen zwarte gaten van gemiddelde grootte zijn gevonden Onderzoekers verklaren het mechanisme van ongeslachtelijke voortplanting bij platwormen
Onderzoekers verklaren het mechanisme van ongeslachtelijke voortplanting bij platwormen Luchtvervuiling maakt ons misschien minder intelligent
Luchtvervuiling maakt ons misschien minder intelligent Common Sense Conduit Bending & Cable Tray Techniques
Common Sense Conduit Bending & Cable Tray Techniques Een verhoudingsgetal in een decimaal getal
Een verhoudingsgetal in een decimaal getal  Onderzoek toont aan dat grafeen bestand is tegen een snelheidskogel
Onderzoek toont aan dat grafeen bestand is tegen een snelheidskogel Proef ingesteld voor Lets die wordt beschuldigd van het uitvoeren van malware
Proef ingesteld voor Lets die wordt beschuldigd van het uitvoeren van malware Hoe u een Absolute Value-functie uitvoert op de TI-83 Plus
Hoe u een Absolute Value-functie uitvoert op de TI-83 Plus
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

