
Wetenschap
Het structurele mysterie van scandiumfluoride geïllustreerd

Krediet:Universiteit van Connecticut
Degene die zei dat regels gemaakt zijn om gebroken te worden, was geen natuurkundige. Als iets niet werkt zoals je denkt dat het zou moeten, ofwel zijn de regels verkeerd, of er is nieuwe natuurkunde te ontdekken. Dat is precies wat Connor Occhialini van UConn, een senior honoursstudent met als hoofdvak natuurkunde en wiskunde, gevonden toen hij begon met het onderzoeken van scandiumfluoride.
Scandiumfluoride is een transparant kristal met een kubusvorm, een bijproduct van de mijnbouw. Het wordt niet commercieel gebruikt en het zou voor niemand bijzonder interessant zijn, behalve één vreemd ding:het krimpt als het opwarmt.
De meeste materialen zwellen op als ze opwarmen. Echt eenvoudige materialen zoals waterstofgas zwellen op omdat de hitte ervoor zorgt dat hun atomen sneller rondzoomen, meer tegen elkaar aanlopen, dus hetzelfde aantal waterstofatomen heeft meer ruimte nodig. Meer gecompliceerde materialen zwellen ook op, daarom blijft uw houten voordeur in de zomer plakken. Maar vaste stoffen zoals hout kunnen niet zo veel opzwellen als een gas, omdat hun atomen nauw met elkaar verbonden zijn tot lange, in elkaar grijpende moleculen, dus ze wiebelen maar wat rond, de deur een beetje opzwellen.
Scandiumfluoride moet iets anders doen, redeneerde Occhialini. Zijn adviseur voor zijn honours natuurkundeproject, Jason Hancock, had gewerkt met scandiumfluoride, en vroeg Occhialini om een model van de dynamiek van het kristal te bestuderen. Scandiumfluoride heeft een vrij eenvoudige structuur:het is een vast kristal, waarbij elk scandiumatoom omringd is door zes fluorines om stapels octaëders (achtzijdige diamanten) te maken. De onderzoekers hoopten dat de eenvoudige structuur gemakkelijk te begrijpen zou zijn. De vreemde 'negatieve thermische uitzetting' van scandiumfluoride begrijpen, ' zoals natuurkundigen de warmtegerelateerde krimp noemen, kan meer algemeen inzicht geven in andere, complexere materialen die hetzelfde doen.

Figuur 1. Hulp, Ik krimp! De zwarte diamanten vertegenwoordigen scandiumfluoridemoleculen. Terwijl ze opwarmen, ze draaien, en de kristalcontracten. Merk op hoe de moleculen nabij het massamiddelpunt (centrale stip) minder bewegen dan de moleculen dichter bij de rand van het kristal. Krediet:Universiteit van Connecticut
De eerste stap van Occhialini was om het probleem te vereenvoudigen. Dus in plaats van een driedimensionaal kristal, hij besloot het te zien als een tweedimensionaal blad.
Elke zwarte diamant vertegenwoordigt een molecuul scandiumfluoride. De scandiumatomen (blauwe stippen) bevinden zich in het midden van elke diamant, en op elke hoek bevindt zich een fluoratoom.
Meestal, bindingen tussen atomen zijn flexibel. Dus in een normale kristallijne vaste stof – calciumfluoride, bijvoorbeeld - de fluor- en calciumatomen zouden allemaal onafhankelijk kunnen wiebelen wanneer het materiaal opwarmt. Terwijl ze wiebelden, ze zouden wat meer ruimte in beslag nemen, en de vaste stof zou opzwellen. Normaal solide gedrag.
Maar Occhialini vroeg zich af of dat misschien niet was wat er gebeurde in scandiumfluoride. Misschien in dit model, hij moet aannemen dat de bindingen die elke fluor met zijn scandium verbinden stijf waren? Zo stijf dat de fluor-scandium bindingen helemaal niet bewegen, dus de diamanten zijn als massieve blokken. De enige plaatsen waar de structuur zou kunnen buigen als hij opwarmt, zijn bij de fluoratomen, die zouden werken als kleine gewrichtjes. Terwijl het kristal opwarmde, de kleine scandiumfluorideblokken zouden rond de fluorines op de hoeken kantelen. Dat is wat je op de foto ziet gebeuren. Je zult merken dat wanneer de diamanten kantelen, de hele structuur wordt kleiner. Het wordt eigenlijk strakker. De blauwe omtrek toont de structuur op zijn koudst, perfect geordende staat, zonder moleculaire beweging. Wanneer de diamanten kantelen, ze nemen een kleiner totaal volume in dan de blauwe omlijning aangeeft. Dit is negatieve thermische uitzetting.
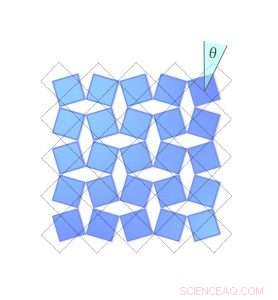
Figuur 2. Hoeveel een scandiumfluoridekristal krimpt, hangt af van hoe ver de moleculen roteren. Hier, de blauwe ruit in de rechterbovenhoek draait met de klok mee, een hoek theta uitvegen. De stippellijnen geven de positie aan toen de hoek nul was. Krediet:Universiteit van Connecticut
Occhialini ontdekte dat je deze krimp wiskundig kunt beschrijven, met alleen de hoek van de kanteling van de moleculen. Hij noemde de hoek Θ (theta). Wanneer de scandiumfluorideblokken over een hoek kantelen, de afstand tussen het midden van elk blok wordt korter met een factor cosinus Θ, en het totale volume van het kristal krimpt.
Om die krimp te berekenen (of, in een normaal materiaal, uitbreiding) in detail, Occhialini voegde een derde term toe aan de klassieke vergelijking die de energie van een trillend kristal beschrijft. De eerste twee termen in de standaardvergelijking beschrijven de potentiële energie die een kristal heeft door de buiging bij elke moleculaire kruising, plus de kinetische rotatie-energie van elk molecuul. De vergelijking van Occhialini beschrijft ook de translationele kinetische energie van de moleculen - niet alleen van ronddraaien, maar ook bewegen naar en weg van hun oorspronkelijke posities als ze roteren. Hoe verder ze van het massamiddelpunt van het kristal verwijderd zijn, hoe meer ze bewegen. Kijk terug naar figuur 1 en let op de stip in het midden; dat is het massamiddelpunt. De diamanten in het midden bewegen nauwelijks ten opzichte ervan, terwijl de diamanten aan de randen veel bewegen. Stel je nu eens voor hoeveel verschil er zou zijn als het kristal miljoenen moleculen zou hebben in plaats van slechts 25. En nu begrijp je hoe belangrijk die derde term zou kunnen zijn voor de energie van het kristal.
Nutsvoorzieningen, moleculen zijn moleculen, ze krimpen niet alleen en blijven daar. Ze zijn constant in beweging, en hoe warmer ze worden, hoe meer ze bewegen. Een deel van Occhialini's inzicht is dat, gemiddeld, de moleculaire structuur wordt buigzamer naarmate het warmer wordt. Dus de moleculen kantelen meer en brengen meer tijd door bij grotere waarden van Θ, dichter bij 45 graden. Nadat Occhialini er samen met Hancock en natuurkunde-promovendi Sahan Handunkanda en Erin Curry even over had nagedacht, ze realiseerden zich dat er een geometrische vorm was met dezelfde wiskundige beschrijving. Het is de spiraalslinger van Archimedes.
Elke draaiing van de spiraal is precies dezelfde afstand van de vorige. Die afstand - de afstand tussen windingen - wordt bepaald door Θ. Stel je een lijn voor die zich uitstrekt van het middelpunt van de bol naar een punt op de spiraal. De hoek tussen die lijn en de pool van de bol is Θ. Zie je het balletje langs de spiraal reizen? Dat is het einde van de denkbeeldige lijn. Naarmate groter wordt, de bal beweegt naar de evenaar. Stel je voor dat de bal de momentane toestand van het scandiumfluoridekristal vertegenwoordigt - de natuurkundigen berekenden het statistische gemiddelde van wat elk molecuul in het kristal doet. Je zult merken dat de bal meer tijd doorbrengt in de buurt van de evenaar van de spiraalvormige bol, dat is, het heeft de neiging om rond te hangen waar Θ groot is. Als de temperatuur van het kristal daalt en de moleculen minder wiebelen, Θ wordt kleiner, hoe meer tijd de bal in de buurt van de pool van de bol doorbrengt en hoe minder het kristal krimpt.
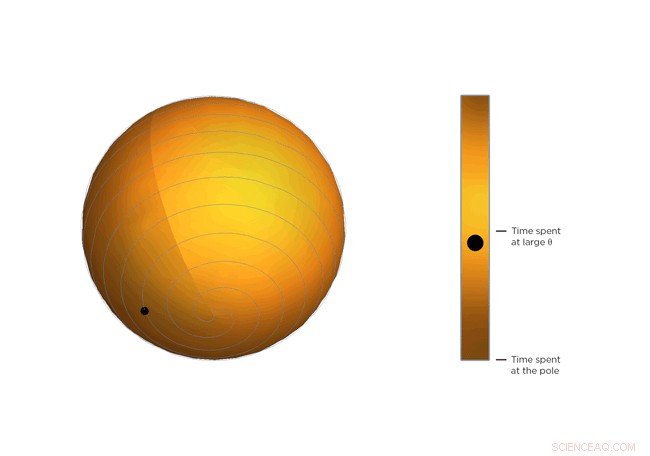
Figuur 3. Draaien en krimpen. De vergelijking die de rotatie van de scandiumfluoridemoleculen beschrijft, is dezelfde als de vergelijking die de beweging van een bal op een spiraalvormige slinger van Archimedes beschrijft. Merk op hoe het meer tijd doorbrengt in grotere hoeken. Krediet:Universiteit van Connecticut
Dus niet alleen kan een heel raar fenomeen van een kristal dat krimpt als het opwarmt worden verklaard door gewoon aan te nemen dat de moleculen stijf zijn, maar het kan worden geïllustreerd met een klassieke geometrische vorm!
Occhialini was nog maar een eerstejaars toen Hancock hem kennis liet maken met de scandiumfluoride-puzzel. Hij moest de wiskunde leren als hij ging, maar na ongeveer twee semesters eraan te hebben gewerkt, had hij de vergelijking bedacht die beschreef wat er aan de hand was. Nu in zijn laatste jaar, hij zegt dat zijn onderzoekservaringen in het laboratorium van Hancock een integraal onderdeel zijn geweest van zijn ervaring als student.
De vergelijking werkt prachtig en verklaart ook bepaalde aspecten van Hancocks experimentele röntgenmetingen.
"Ik heb veel meer geleerd door onderzoek te doen dan welke cursus me ook had kunnen geven, ' zegt Occhialini.
 Heeft de opwarming van het Noordpoolgebied invloed op het extreme weer in het VK?
Heeft de opwarming van het Noordpoolgebied invloed op het extreme weer in het VK? Geregenereerde bossen compenseren 12% van de CO2-uitstoot in het Braziliaanse Amazonegebied in 33 jaar
Geregenereerde bossen compenseren 12% van de CO2-uitstoot in het Braziliaanse Amazonegebied in 33 jaar Is er een duidelijk verband tussen vogels en dinosaurussen?
Is er een duidelijk verband tussen vogels en dinosaurussen?  De temperatuur en het klimaat in het oude Mesopotamië
De temperatuur en het klimaat in het oude Mesopotamië Blikseminslagen doden 16 op bruiloft in Bangladesh
Blikseminslagen doden 16 op bruiloft in Bangladesh
Hoofdlijnen
- 10 fascinerende feiten over de nieuwe levensboom-evolutiekaart
- Vreemde ondernemingen:mierenkoninginnen begraven doden om ziekte te voorkomen
- In het verleden werpen helpt de toekomst van de visserij te onthullen
- Wat zou er gebeuren als de cel geen DNA had?
- Wat is het belang van nucleïnezuren?
- Wat als Homeostase mislukt?
- Rollen van celorganellen in mitose
- Zijn linkshandigen snellere denkers dan rechtshandigen?
- Hoe maak je een 3D-plant eukaryotisch celmodel
- Hogedruksleutel tot aansteker, sterkere metaallegeringen, wetenschappers vinden

- Topologie werpt nieuw licht op synchronisatie in netwerken van hogere orde

- Hebben cellen exotische vibrerende eigenschappen?

- Quantumsimulator faciliteert onderzoek naar theoretische supermaterialen
- Meerkanaals vectoriële holografische weergave en codering

 Wat voor soort dieren bevinden zich in regio Noord-Noord Texas
Wat voor soort dieren bevinden zich in regio Noord-Noord Texas  Nieuw artikel toont voordelen van kustherstel in Louisiana voor koolstofvastlegging in de bodem
Nieuw artikel toont voordelen van kustherstel in Louisiana voor koolstofvastlegging in de bodem Een algemeen verbod op giftige chemicaliën voor altijd is goed voor mens en dier
Een algemeen verbod op giftige chemicaliën voor altijd is goed voor mens en dier Wat zijn oppervlaktestromen veroorzaakt door?
Wat zijn oppervlaktestromen veroorzaakt door?  Wat zijn de aanpassingen die een hagedis toelaat om in de woestijn te leven?
Wat zijn de aanpassingen die een hagedis toelaat om in de woestijn te leven?  Onderzoek naar de stabiliteit van hoogenergetische materialen
Onderzoek naar de stabiliteit van hoogenergetische materialen Hoe om te berekenen pond per lineaire inch
Hoe om te berekenen pond per lineaire inch Poll:Energiebesparende gewoonten variëren in populariteit
Poll:Energiebesparende gewoonten variëren in populariteit
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

