
Wetenschap
Nieuw inzicht in het bewijzen van een miljoenendollarprobleem:de Riemann-hypothese (update)
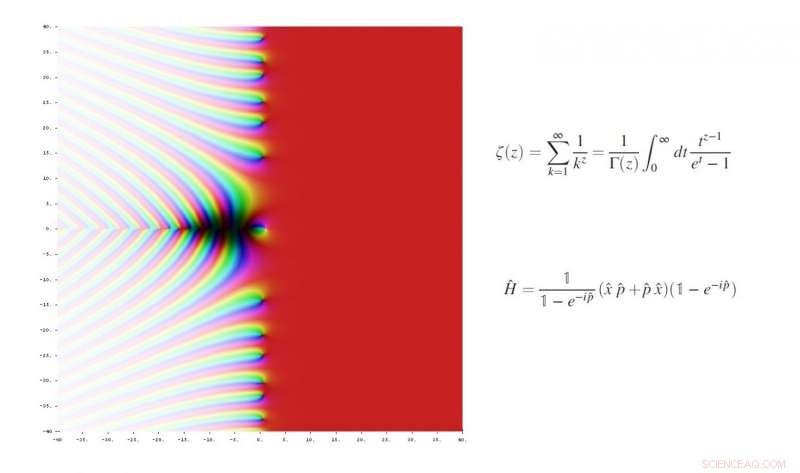
in 1859, Riemann veronderstelde dat de niet-triviale nullen van de Riemann-zetafunctie op de verticale lijn (½ + it) op het complexe vlak liggen, waarbij het reële deel altijd ½ is. Krediet:Jan Homann, Wikimedia Commons. Boven:Riemann zeta-functie. Onder:De nieuwe operatorfunctie.
(Phys.org)—Onderzoekers hebben ontdekt dat de oplossingen van een beroemde wiskundige functie, de Riemann-zetafunctie genaamd, overeenkomen met de oplossingen van een andere, ander soort functie die het misschien gemakkelijker maakt om een van de grootste problemen in de wiskunde op te lossen:de Riemann-hypothese. Als de resultaten rigoureus kunnen worden geverifieerd, dan zou het eindelijk de Riemann-hypothese bewijzen, wat een $1 waard is, 000, 000 Millenniumprijs van het Clay Mathematics Institute.
Terwijl de Riemann-hypothese teruggaat tot 1859, de afgelopen 100 jaar hebben wiskundigen geprobeerd een operatorfunctie te vinden zoals die hier is ontdekt, omdat het wordt beschouwd als een belangrijke stap in het bewijs.
"Voor zover we weten, dit is de eerste keer dat een expliciete en misschien verrassend relatief eenvoudige operator is geïdentificeerd waarvan de eigenwaarden ['oplossingen' in matrixterminologie] exact overeenkomen met de niet-triviale nullen van de Riemann-zetafunctie, "Dorje Brody, een wiskundig fysicus aan de Brunel University London en co-auteur van de nieuwe studie, vertelde Phys.org .
Wat nog moet worden bewezen, is de tweede belangrijke stap:dat alle eigenwaarden reële getallen zijn in plaats van denkbeeldige. Als toekomstig werk dit kan bewijzen, dan zou het eindelijk de Riemann-hypothese bewijzen.
Brody en zijn co-auteurs, wiskundige fysici Carl Bender van de Washington University in St. Louis en Markus Müller van de University of Western Ontario, hebben hun werk gepubliceerd in een recent nummer van Fysieke beoordelingsbrieven .
Afstand tussen priemgetallen
De Riemann-hypothese heeft zo'n sterke aantrekkingskracht omdat deze nauw verbonden is met de getaltheorie en, vooral, de priemgetallen. In zijn artikel uit 1859, De Duitse wiskundige Bernhard Riemann onderzocht de verdeling van de priemgetallen - of meer precies, het probleem "gegeven een geheel getal N, hoeveel priemgetallen zijn er die kleiner zijn dan N?"
Riemann vermoedde dat de verdeling van de priemgetallen kleiner dan N gerelateerd is aan de niet-triviale nullen van wat nu de Riemann zeta-functie wordt genoemd, ( s ). (De nullen zijn de oplossingen, of de waarden van s waardoor de functie gelijk is aan nul. Hoewel het voor wiskundigen gemakkelijk was om te zien dat er altijd nullen zijn s een negatief even getal is, deze nullen worden beschouwd als triviale nullen en zijn niet het interessante deel van de functie.)
Riemann's hypothese was dat alle niet-triviale nullen langs een enkele verticale lijn liggen (½ + het ) in het complexe vlak - wat betekent dat hun echte component altijd ½ is, terwijl hun denkbeeldige component l varieert als je op en neer gaat.
In de afgelopen 150 jaar is wiskundigen hebben letterlijk biljoenen niet-triviale nullen gevonden, en ze hebben allemaal een reële of component van ½, precies zoals Riemann dacht. Er wordt algemeen aangenomen dat de Riemann-hypothese waar is, en er is veel werk verzet op basis van deze veronderstelling. Maar ondanks intensieve inspanningen, de Riemann-hypothese - dat alle oneindig veel nullen op deze enkele lijn liggen - is nog niet bewezen.
Identieke oplossingen
Een van de nuttigste aanwijzingen voor het bewijzen van de Riemann-hypothese is afkomstig uit de functietheorie, waaruit blijkt dat de waarden van het imaginaire deel, t , waarbij de functie verdwijnt, zijn discrete getallen. Dit suggereert dat de niet-triviale nullen een reeks reële en discrete getallen vormen, wat net als de eigenwaarden van een andere functie een differentiaaloperator is, die veel wordt gebruikt in de natuurkunde.
In de vroege jaren 1900, deze overeenkomst bracht sommige wiskundigen ertoe zich af te vragen of er echt een differentiaaloperator bestaat waarvan de eigenwaarden exact overeenkomen met de niet-triviale nullen van de Riemann-zetafunctie. Tegenwoordig wordt dit idee het vermoeden van Hilbert-Pólya genoemd, genoemd naar David Hilbert en George Pólya - ondanks het feit dat geen van beiden er iets over publiceerde.
"Aangezien er geen publicatie is van Hilbert of Pólya, de exacte verklaring van het Hilbert-Pólya-programma is tot op zekere hoogte onderhevig aan interpretatie, maar het is waarschijnlijk niet onredelijk om te zeggen dat het uit twee stappen bestaat:(a) zoek een operator waarvan de eigenwaarden overeenkomen met de niet-triviale nullen van de Riemann zeta-functie; en (b) bepalen of de eigenwaarden reëel zijn, ' zei Brody.
"De belangrijkste focus van ons werk tot nu toe was op stap (a), " zei hij. "We hebben een operator geïdentificeerd waarvan de eigenwaarden exact overeenkomen met de niet-triviale nullen van de Riemann zeta-functie. We beginnen pas na te denken over stap (b), en inderdaad hoe deze uitdaging aan te gaan. Of het moeilijk of gemakkelijk zal zijn om de ontbrekende stappen naar stap (b) in te vullen, op dit moment kunnen we niet speculeren - er is meer werk nodig om een beter idee te krijgen van de omvang van de moeilijkheidsgraad die ermee gemoeid is."
de exploitant
Een van de interessante dingen van de nieuw ontdekte operator is dat hij nauwe banden heeft met de kwantumfysica.
In 1999, toen wiskundige fysici Michael Berry en Jonathan Keating het vermoeden van Hilbert-Pólya onderzochten, ze maakten nog een belangrijke gissing. Als een dergelijke exploitant bestaat, ze zeiden, dan moet het overeenkomen met een theoretisch kwantumsysteem met bepaalde eigenschappen. Dit wordt nu het vermoeden van Berry-Keating genoemd. Maar niemand heeft ooit eerder zo'n systeem gevonden, en dit is een tweede belangrijk aspect van het nieuwe werk.
"We hebben een kwantisatievoorwaarde geïdentificeerd voor de Berry-Keating Hamiltoniaan, dus in wezen de geldigheid van het vermoeden van Berry-Keating verifiëren, ' zei Brody.
Hamiltonianen worden vaak gebruikt om de energie van fysieke systemen te beschrijven. De nieuwe exploitant, echter, lijkt geen fysiek systeem te beschrijven, maar is eerder een puur wiskundige functie.
"Misschien is het teleurstellend, maar zo'n Hamiltoniaan lijkt op geen enkele voor de hand liggende manier fysieke systemen weer te geven; of in ieder geval tot dusver hebben we geen indicatie gevonden dat onze Hamiltoniaan overeenkomt met een fysiek systeem, ' zei Brody.
"Maar men zou dan kunnen vragen 'waarom publiceren in? PRL ?' Het antwoord is dat veel van de technieken die in onze paper voor sommige heuristische analyses worden gebruikt en die suggestief zijn, zijn ontleend aan technieken van de pseudo-Hermitiaanse PT-symmetrische kwantumtheorie die in de afgelopen 15 jaar of zo is ontwikkeld. Het conventionele begrip van het vermoeden van Hilbert-Pólya is dat de operator (Hamiltonian) Hermitiaans moet zijn, en men koppelt dit natuurlijk aan de kwantumtheorie waarbij van Hamiltonianen conventioneel wordt geëist dat ze Hermitisch zijn. We stellen een pseudo-Hermitische vorm van het Hilbert-Pólya-programma voor, die ons de moeite waard lijkt om verder te onderzoeken."
Echte oplossingen
Nu is de grootste uitdaging die overblijft om aan te tonen dat de eigenwaarden van de operator reële getallen zijn.
In het algemeen, de onderzoekers zijn optimistisch dat de eigenwaarden echt zijn, en in hun paper presenteren ze een sterk argument hiervoor op basis van PT-symmetrie, een concept uit de kwantumfysica. In principe, PT-symmetrie zegt dat je de tekens van alle vier de componenten van ruimte-tijd kunt veranderen (drie ruimte- of "pariteits"-dimensies en één tijdsdimensie), en, als het systeem PT-symmetrisch is, dan ziet het resultaat er hetzelfde uit als het origineel.
Hoewel de natuur in het algemeen niet PT-symmetrisch is, de operator die de fysici hebben geconstrueerd. Maar nu willen de onderzoekers aantonen dat deze symmetrie wordt doorbroken. Zoals ze in hun paper uitleggen, als kan worden aangetoond dat de PT-symmetrie is verbroken voor het imaginaire deel van de operator, dan zou volgen dat de eigenwaarden allemaal reële getallen zijn, die uiteindelijk het langverwachte bewijs van de Riemann-hypothese zou vormen.
Over het algemeen wordt aangenomen dat een bewijs van de Riemann-hypothese zeer nuttig zal zijn in de informatica, vooral cryptografie. De onderzoekers willen ook bepalen wat hun resultaten eigenlijk kunnen betekenen voor het begrijpen van meer fundamentele wiskundige principes.
"Wat we tot nu toe hebben onderzocht, bevat weinig getaltheoretische inzichten; terwijl je zou verwachten dat, gezien het belang ervan in de getaltheorie, zeker zou elke poging die met succes vooruitgang boekt bij het vaststellen van de Riemann-hypothese getaltheoretische inzichten bieden, "Zei Brody. "Natuurlijk hoeft dit helemaal niet het geval te zijn, maar desalniettemin zou het interessant zijn om te onderzoeken of een van de dynamische aspecten van het hypothetische systeem dat door onze Hamiltoniaan wordt beschreven, verband zou kunnen houden met bepaalde getaltheoretische resultaten. In dit verband, semi-klassieke analyse van onze Hamiltoniaan zou een van de volgende doelstellingen zijn."
© 2017 Fys.org
 Hoe beïnvloedt bodem de PH van water?
Hoe beïnvloedt bodem de PH van water?  Onderzoekers valideren klinische haalbaarheid voor op CRISPR gebaseerde COVID-19-tests op het zorgpunt
Onderzoekers valideren klinische haalbaarheid voor op CRISPR gebaseerde COVID-19-tests op het zorgpunt Maken of breken:nieuwe omkeerbare techniek produceert acylfluoride met behulp van zeldzaam metaal
Maken of breken:nieuwe omkeerbare techniek produceert acylfluoride met behulp van zeldzaam metaal Welke chemicaliën zijn schadelijk voor rubberafdichtingen?
Welke chemicaliën zijn schadelijk voor rubberafdichtingen?  Poreuze vloeistof bevat grotere moleculen
Poreuze vloeistof bevat grotere moleculen
 CO2-tekort:waarom een chemisch probleem kan leiden tot meer lege schappen
CO2-tekort:waarom een chemisch probleem kan leiden tot meer lege schappen Luchtvervuiling leidt tot meer elektriciteitsverbruik, studie suggereert:
Luchtvervuiling leidt tot meer elektriciteitsverbruik, studie suggereert: Witte lijn van algendoden markeert een stijging in de Chileense aardbeving van 2016
Witte lijn van algendoden markeert een stijging in de Chileense aardbeving van 2016 Overlevenden, familieleden, vrijwilligers verbinden online voor Irma aid
Overlevenden, familieleden, vrijwilligers verbinden online voor Irma aid Voedselketens in het bladverliezende woud
Voedselketens in het bladverliezende woud
Hoofdlijnen
- Inheemse vissoorten lopen gevaar na verwijdering van water uit de Colorado-rivier
- Maken regenachtige dagen je echt down?
- Gewassen evolueerden 10 millennia eerder dan gedacht
- Overeenkomsten tussen verbranding en cellulaire ademhaling
- Kun je iemand echt doodsbang maken?
- Internationale concurrentiebenchmarks metagenomics-software
- Fun Biology Presentatie Onderwerpen
- Nieuw boek van biologen beschrijft een nieuw tijdperk in de studie van evolutie
- Zenuwen controleren de bacteriële gemeenschap van het lichaam
 Japanse miljardair zegt dat tweet over gratis geld het meest is gedeeld aller tijden
Japanse miljardair zegt dat tweet over gratis geld het meest is gedeeld aller tijden Onderzoek naar chemische variaties van carbonaatmineralen om de oliewinning te verbeteren
Onderzoek naar chemische variaties van carbonaatmineralen om de oliewinning te verbeteren Effectieve temperaturen verbinden evenwichts- en niet-evenwichtssystemen
Effectieve temperaturen verbinden evenwichts- en niet-evenwichtssystemen Ingenieurs 3D-printen een geminiaturiseerde spectrometer
Ingenieurs 3D-printen een geminiaturiseerde spectrometer Het is absoluut noodzakelijk om natuurlijke processen op te nemen om ecologische krachten te benutten en herstel van ecosystemen van koraalriffen te stimuleren
Het is absoluut noodzakelijk om natuurlijke processen op te nemen om ecologische krachten te benutten en herstel van ecosystemen van koraalriffen te stimuleren Octupole hoektoestand in een driedimensionaal topologisch circuit
Octupole hoektoestand in een driedimensionaal topologisch circuit Machine-learning aardbevingsvoorspelling in laboratorium veelbelovend
Machine-learning aardbevingsvoorspelling in laboratorium veelbelovend Koele daken kunnen Californische steden helpen beschermen tegen hittegolven
Koele daken kunnen Californische steden helpen beschermen tegen hittegolven
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






