
Wetenschap
Naar nieuwe IT-apparaten met stabiele en transformeerbare solitons
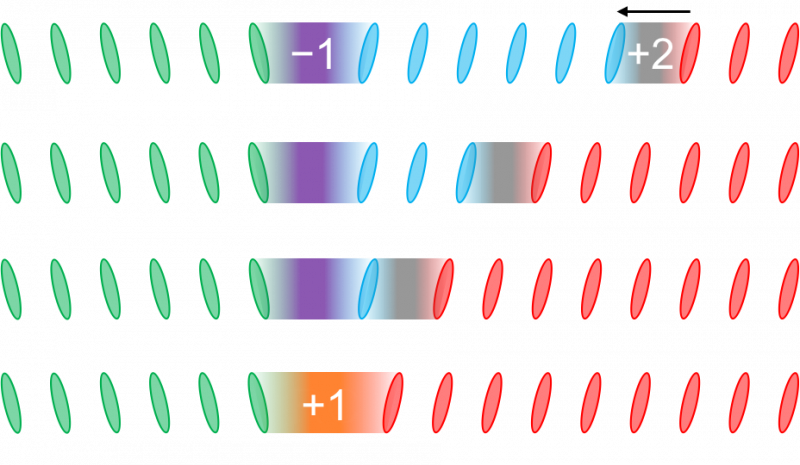
Wanneer twee solitons elkaar ontmoeten, ze wisselen van type, volgens een quaternair systeem dat uit slechts vier cijfers bestaat:-1, 0, 1 en 2. In dit geval ontmoet een -1 soliton een 2 soliton om een 1 soliton te vormen. Krediet:IBS
Onvermijdelijk, elke digitale informatie die we over de hele wereld verzenden, kan verloren gaan. Lange wegen reizen in draden, het initiële signaal vervalt en verstrooit door te botsen met onzuiverheden en naburige elektromagnetische velden. Daarom, voorbij elk stukje van uw gewenste bericht, het is noodzakelijk om andere verborgen stukjes informatie te verzenden die controleren op fouten en actie ondernemen in geval van verlies; terwijl apparaten steeds kleiner worden, dit probleem wordt belangrijker. Wetenschappers van het Center for Artificial Low Dimensional Electronic (CALDES), binnen het Instituut voor Basiswetenschappen (IBS) streven naar innovatieve manieren om tot een stabielere informatieoverdracht te komen. Een van hun onderzoeksinteresses richt zich op zelfversterkende solitaire golfpakketten die solitonen worden genoemd, die stabiel zijn, ongeacht de omgeving. In hun meest recente artikel toonden ze aan dat solitonen kunnen worden gemanipuleerd en schetsen ze hoe ze voor logische bewerkingen kunnen worden gebruikt. Hun experimenten en modellen zijn gepubliceerd in Natuurfysica en de weg vrijmaken voor een nieuw gebied van elektronica:Solitoniek.
Natuurkundigen weten dat een mogelijke oplossing voor het probleem van signaalverzwakking of ruis als gevolg van externe interferenties kan komen van een wiskundig concept dat topologie wordt genoemd. Het is gerelateerd aan eigenschappen die niet worden beïnvloed door een verandering in vorm. Bijvoorbeeld, geloof het of niet, een bal en een potlood zijn topologisch hetzelfde, maar anders dan een donut. Dit is zo omdat, met enige fantasie, je kunt de bal in de vorm van het potlood vormen. Echter, als je een gat in de bal maakt, het wordt een totaal ander topologisch object. Gaten definiëren de topologische toestand, ze kunnen bewegen in het materiaal, maar hun aantal verandert niet, zelfs niet onder de aanwezigheid van duwende en trekkende krachten. Een soortgelijk concept zou in de IT kunnen worden gebruikt om de informatiestroom te beschermen tegen externe interferenties en onzuiverheden en de stabiliteit ervan over langere afstanden en in de tijd te garanderen. Het klinkt als een geweldige eigenschap, maar, paradoxaal genoeg, het is ook zijn eigen grootste vijand:de verzonden informatie is te stabiel, op een manier die eigenlijk te moeilijk te wijzigen en te gebruiken is. Dat leek het trieste einde van het verhaal te zijn, totdat IBS-wetenschappers een manier demonstreerden om het verzonden signaal te manipuleren en mogelijk toe te passen op moderne elektronica.
Een van de belangrijkste componenten van de fysica van het topologische systeem is de soliton, een extreem stabiel solitair golfpakket van energie, die door sommige 1D-materialen reist zonder zijn vorm en energie te verliezen, een beetje als een tsunami-golf. Wetenschappers begonnen topologische solitonen te bestuderen in de jaren 80, maar werden afgeschrikt door de schijnbaar onmogelijkheid om ze te manipuleren.
Vorig jaar, IBS-wetenschappers onderzochten de eigenschappen van solitonen op een dubbele keten van indiumatomen die bovenop een siliciumoppervlak waren geplaatst en ontdekten dat solitonen in drie vormen kunnen bestaan. "In topologische zin, het is alsof je een donut hebt met veel gaten, waarbij elk gat drie verschillende vormen kan hebben die overeenkomen met de drie soorten solitons, " legt YEOM Han Woong uit, de hoofdauteur van deze studie. "Natuurkundigen werkten vroeger met solitons (gaten) van hetzelfde type en de operaties die je ermee kon doen waren beperkt, maar nu hebben we een grotere kans om met hen te spelen."
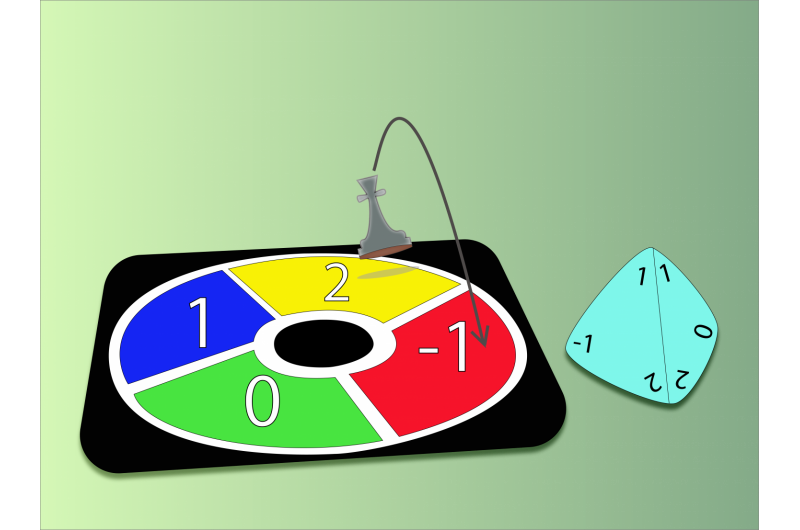
Terwijl de binaire code die in onze huidige computers wordt gebruikt, bestaat uit nullen en enen. Een quaternair systeem, zoals die voorgesteld door IBS-wetenschappers, bestaat uit vier cijfers (0, 1, 2 en -1) en zou meer bewerkingen mogelijk maken. De onderzoekers modelleerden solitonenverslaving. Bijvoorbeeld, een soliton vertegenwoordigd door het getal 2, en een andere vertegenwoordigd door het nummer 1 kan worden toegevoegd om een nieuwe soliton te vormen (n. -1). Inderdaad, in dit 4-base systeem, 2+1 maakt -1, en het is gemakkelijk te begrijpen waarom als je je een klein en rond "ganzenspel" voorstelt, waarbij je met de klok mee (of tegen de klok in) beweegt, afhankelijk van het getal dat je krijgt door een vierzijdige dobbelsteen met de getallen 0 te gooien, 1, 2 en -1. Als je in het vak n. 2 en je krijgt n. 1 op de dobbelstenen, je gaat naar het -1 vierkant. Krediet:IBS
In deze nieuwe studie Yeom en zijn team bewezen, experimenteel, dat schakelen tussen deze solitonen mogelijk is. Ze merkten op dat wanneer twee solitons elkaar ontmoeten, ze resulteren in een andere soliton, met andere woorden, ze ontdekten dat solitonen kunnen worden getransformeerd, en toch immuun blijven voor de gebreken van het medium. "Tot nu toe konden solitons alleen in paren worden gemaakt of vernietigd, geen andere manipulaties mogelijk waren, maar we hebben laten zien dat deze solitonen van de ene naar de andere kunnen worden omgeschakeld, en zelfs gebruikt voor logische bewerkingen", vervolgt Yeom.
Deze drie soorten solitonen kunnen ook worden weergegeven door cijfers (1, -1 en 2) en de conditie zonder solitonen als nul (0), het creëren van een quaternair wiskundig systeem. De vier cijfers kunnen vervolgens worden gebruikt voor wiskundige berekeningen.
Quaternaire cijfersystemen, en meercijferige systemen in het algemeen, hebben verschillende voordelen ten opzichte van de binaire (0, 1) systeem dat we momenteel gebruiken. Ze maken meer operaties en informatieopslag mogelijk in minder ruimte en kunnen ons een stap dichter bij hersenachtige apparaten brengen, die de manier nabootsen waarop informatie wordt berekend en opgeslagen door onze neuronale circuits.
Het openen van een nieuw gebied van elektronica, nagesynchroniseerde solitoniek, IBS-wetenschappers stellen zich nieuwe generatie IT-apparaten voor die silicium en solitonen combineren. "We gebruiken solitonen die in indiumatomen reizen op een siliciumoppervlak, en we stellen ons voor dat deze structuur die zou kunnen worden geïmplementeerd in de huidige siliciumapparaten, hybride systemen creëren, " legt KIM Tae-Hwan uit, eerste auteur van deze studie.
 "What is an Arrhenius Acid?
"What is an Arrhenius Acid? Leren hoe boor verdampt, zal de technologieën voor waterontzilting verbeteren
Leren hoe boor verdampt, zal de technologieën voor waterontzilting verbeteren Diepblauwe organische lichtemitterende diodes op basis van een doublet-emissie cerium(III)-complex
Diepblauwe organische lichtemitterende diodes op basis van een doublet-emissie cerium(III)-complex Verschillen in eigenschappen van halogenen en waterstof
Verschillen in eigenschappen van halogenen en waterstof Wetenschappers ontwikkelen een nieuw zelfherstellend interactief hydrogel-touchpad tussen mens en machine
Wetenschappers ontwikkelen een nieuw zelfherstellend interactief hydrogel-touchpad tussen mens en machine
 Hoe u uw broeikasgasvoetafdruk kunt neutraliseren
Hoe u uw broeikasgasvoetafdruk kunt neutraliseren Schade gemeld als aardbeving met een kracht van 5,4 op Puerto Rico
Schade gemeld als aardbeving met een kracht van 5,4 op Puerto Rico Wetenschappers beschrijven de verspreiding van bodemmicro-organismen
Wetenschappers beschrijven de verspreiding van bodemmicro-organismen Onderzoek suggereert dat ontsmettingsmiddelen een zeer lage langetermijnimpact op de bodemgezondheid hebben
Onderzoek suggereert dat ontsmettingsmiddelen een zeer lage langetermijnimpact op de bodemgezondheid hebben Vingerafdrukken van de originele bouwstenen van de aarde ontdekt in diamanthoudende rotsen
Vingerafdrukken van de originele bouwstenen van de aarde ontdekt in diamanthoudende rotsen
Hoofdlijnen
- Top tien feiten over de menselijke blaas
- Hoe erg is zwarte schimmel,
- Wat is het Geluksproject?
- Structuur van het hart Cell
- Hoe handhaaft het plasmamembraan homeostase?
- Onderzoek naar schapengenen kan helpen om gezondere dieren te fokken
- Gemengde organisatie van darmbacteriën wordt onthuld door microbioombeeldvormingstechnologie
- Hoe de percentages van adenine in een DNA-streng te berekenen
- Hoe toxoplasmose immuuncellen uitbuit om de hersenen te bereiken?
 Nieuwe Samsung-telefoon:innovatie draait om opvouwbaar scherm
Nieuwe Samsung-telefoon:innovatie draait om opvouwbaar scherm Jonge mannen over sexting:het is normaal, maar ingewikkeld
Jonge mannen over sexting:het is normaal, maar ingewikkeld Oude Egyptische handleiding onthult nieuwe details over mummificatie
Oude Egyptische handleiding onthult nieuwe details over mummificatie NASA krijgt een infrarood babyfoto van de tropische storm Kristy
NASA krijgt een infrarood babyfoto van de tropische storm Kristy Feiten over dinosaurussen voor kinderen
Feiten over dinosaurussen voor kinderen Een versnelling van kustoverslag over de hele wereld
Een versnelling van kustoverslag over de hele wereld Inkt met tinnen nanodeeltjes kan toekomstige printplaten printen
Inkt met tinnen nanodeeltjes kan toekomstige printplaten printen Plasmastroom nabij het oppervlak van de zon verklaart zonnevlekken, andere zonneverschijnselen
Plasmastroom nabij het oppervlak van de zon verklaart zonnevlekken, andere zonneverschijnselen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






