Onderzoekers ontdekten dat epitheelcellen - die het oppervlak van veel menselijke organen bedekken - een nieuwe geometrische vorm gebruiken, de scutoïde, zodat de weefsels kunnen buigen. Universiteit van Sevilla

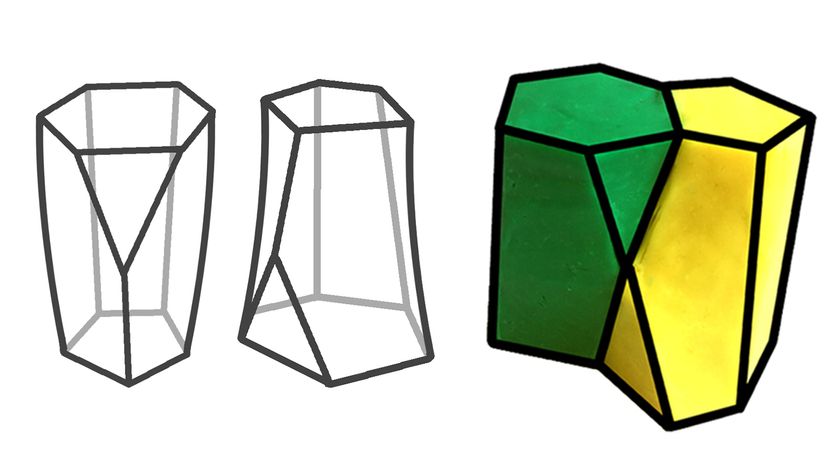
Tenzij je onder een langwerpige sferoïde hebt geleefd, je hebt waarschijnlijk gehoord van de nieuwste ontdekking in vormen:de scutoid. Een team van Spaanse biologen van de Universiteit van Sevilla heeft de scutoid gemodelleerd om te bepalen hoe epitheelcellen zich samenpakken om de barrières van de huid te vormen, organen en bloedvaten.

De onderzoekers gebruikten eenvoudigweg wiskunde om een ​​vorm in de natuur te veronderstellen - een vorm die nodig is voor de constructie van meercellige organismen. Toen duidelijk werd dat de vorm nieuw was voor de geometrie, ze noemden het naar het schildje, het deel van de thorax van een kever dat vaag lijkt op de pas gedoopte scutoid.

In het voorbeeld van de scutoid, we kunnen veel intuïtief aanvoelen over de ontdekking van nieuwe vormen:waar ze vandaan komen en waarom we ze om te beginnen zoeken.

De meest basale vorm van het ontdekken van vormen is ze simpelweg in de natuurlijke wereld te bekijken. De zeshoek (een zeshoekige veelhoek), bijvoorbeeld, komt in alles voor, van zeepbellen en honingraten tot de wolken van Saturnus. Zoals schrijver Phillip Ball onderzocht in het Nautilus-artikel "Why Nature Prefers Hexagons, " legt hij uit hoe het een geometrisch ideale vorm is voor een aantal functies. de zeshoek is voortgekomen uit fysieke interacties en biologische evolutie. Mensen kwamen net langs en noemden het.

Andere vormen komen minder vaak voor in de natuur, maar komen gemakkelijk voort uit geometrie - of zelfs ongeïnformeerde verbeelding. Rechte hoeken, bijvoorbeeld, zijn zeldzaam in de natuurlijke wereld. Een wandeling door de wildernis levert je geen vierkanten en rechthoeken op. Inderdaad, onderzoek wijst uit dat we in plaats daarvan misschien vastgebonden zijn om natuurlijke rondingen te verkiezen boven rechte lijnen. Toch bouwen we nog steeds kubussen en gebruiken ze om de wereld opnieuw te maken.

Er is een verbroken verbinding, echter, tussen de soorten vormen die kunnen worden geconceptualiseerd en die welke in de natuur kunnen worden gevonden of gereproduceerd. Perfecte cirkels, bijvoorbeeld, bestaan ​​niet in ons materiële rijk. Vanuit een puur wiskundig standpunt, we kunnen gemakkelijk een reeks punten in een vlak construeren die op gelijke afstand van een bepaald punt liggen. Maar, in werkelijkheid, zelfs de fijnst bewerkte cirkels en bollen voldoen niet aan wiskundige perfectie. Zelfs de gyroscopische kwartsrotors die zijn gebouwd voor NASA's Gravity Probe B zijn nog steeds minder dan drie tienmiljoenste van een inch verwijderd van perfectie.

de scutoïde, echter, lijkt echt te bestaan. We kunnen misschien niet zien het, maar wetenschappers hebben het wiskundig gemodelleerd als een oplossing voor een biologisch probleem. Als zodanig, als de wetenschap op een dag de scutoid zou verlaten ten gunste van een andere oplossing, de vorm zelf blijft geometrisch bestaan.

Dus, verversen, men kan vormen ontdekken door ze in de natuur te spotten, hun bestaan ​​in de natuur afleiden of door middel van een oefening in zuivere wiskunde. Het is zeldzaam tegenwoordig, maar vormjagers duiken af ​​en toe op een nieuw type vijfhoek of zelfs een nieuwe klasse van vaste vormen.

Dus hoe dan ook, ga erop uit en kijk wat je kunt vinden - maar houd er rekening mee dat we al heel wat wiskundige vormen in ons bestand hebben. De trapezo-ruitvormige dodecaëder is al bezet - en Clickhole heeft dibs op de Triquandle.

Dat is nu onmogelijk

Optische illusies zoals de Penrose-driehoek maken gebruik van dezelfde visuele neigingen die achterwaartse letters zo'n gemakkelijke fout maken op de vroege basisschool. EEN P en een Q op papier duidelijk anders zijn, maar als we ze interpreteren als 3D-beelden, dan zijn het gewoon twee aanzichten van hetzelfde object. De Penrose-driehoek kan niet werkelijk bestaan ​​in de 3D-ruimte, maar we nemen het waar als een 3D-object en deze verwarrende figuur is nog steeds gecomponeerd in de vorm van een driehoek. Nog altijd, zoals Lionel en Roger Penrose bewezen, jij kan ontdek en benoem dergelijke objecten - zelfs als Oscar Reutersvärd het jaren eerder heeft gemaakt.