
Wetenschap
Hoeveel moleculen N2 -gas bevinden zich in een monster van 500,0 ml bij 780 mmHg en 135 C?
1. Converteren eenheden
* volume (v): 500,0 ml =0,500 l
* druk (p): 780 mmHg =1,03 atm (met behulp van de conversiefactor 1 atm =760 mmHg)
* temperatuur (t): 135 ° C =408 K (met behulp van de conversiefactor k =° C + 273.15)
2. Ideale gaswet
De ideale gaswet wordt uitgedrukt als:
PV =NRT
Waar:
* P =druk (in atm)
* V =volume (in l)
* n =aantal mol
* R =ideale gasconstante (0,0821 l · atm/mol · k)
* T =temperatuur (in k)
3. Oplossen voor het aantal mol (n)
Herschik de ideale gaswet om op te lossen voor n:
n =PV / RT
Vervang de bekende waarden:
n =(1,03 atm) (0,500 l) / (0,0821 l · atm / mol · k) (408 k)
n ≈ 0,0155 mol
4. Bereken het aantal moleculen
* Avogadro's nummer: Eén mol van elke stof bevat 6,022 x 10^23 moleculen (het nummer van Avogadro).
* Bereken moleculen:
Aantal moleculen =(0,0155 mol) * (6.022 x 10^23 moleculen/mol)
Aantal moleculen ≈ 9,34 x 10^21 moleculen
Daarom zijn er ongeveer 9,34 x 10^21 moleculen van N2 -gas in het monster van 500,0 ml.
 Bosbranden woeden in het snikhete Californië en dwingen duizenden te vluchten
Bosbranden woeden in het snikhete Californië en dwingen duizenden te vluchten Inzicht in de 'kern van onderconsumptie':hoe een nieuwe trend de consumentencultuur uitdaagt
Inzicht in de 'kern van onderconsumptie':hoe een nieuwe trend de consumentencultuur uitdaagt  NASA-NOAA-satelliet ziet een strakke circulatie in tropische storm Kiko
NASA-NOAA-satelliet ziet een strakke circulatie in tropische storm Kiko Kluizenaar of niet? Wetenschappers gebruiken Twitter om spinnenvragen aan te pakken
Kluizenaar of niet? Wetenschappers gebruiken Twitter om spinnenvragen aan te pakken  Wat is er ter wereld die je ziet, maar het kan ruiken?
Wat is er ter wereld die je ziet, maar het kan ruiken?
Hoofdlijnen
- Wat zijn de overeenkomsten en verschillen tussen menselijke cellen van bacteriën?
- Wat zijn de verschillen van eenvoudig en gestratificeerd weefsel?
- Nieuwe gegevens laten zien hoe staten het doen in de wetenschap
- Heeft een mier slechts één type cel erin?
- Is er eerder enige vorm van exploratie op Mercurius gedaan
- Welk type celdeling komt voor in kankercellen?
- Wat is de functie van cytoplasma in een cel?
- Wat omsluit de mitochondria?
- Bewaakt een celwand voedsel en water in cel?
- Duurzame waterkwaliteitssensor gemaakt van van mensenhaar afgeleide koolstofstippen

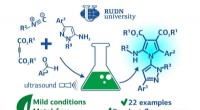
- Chemicus stelt milieuvriendelijke synthese van fluorescerende verbindingen voor medicijnen voor
- Splashdown:Supersonische koudmetaalverbinding in 3D

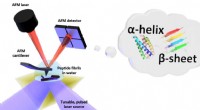
- De vorm in water:eerste nanoschaalmetingen van het vouwen van biomoleculen in vloeistof
- Wanneer minder meer is:Designer-spleten maken glasachtige materialen veel sterker

 Wat is de molaire massa van HNO3?
Wat is de molaire massa van HNO3?  Kunnen meisjes beter lezen dan jongens? Als dat zo is, kunnen genderstereotypen hiervan de oorzaak zijn
Kunnen meisjes beter lezen dan jongens? Als dat zo is, kunnen genderstereotypen hiervan de oorzaak zijn  Wat valt buiten de wetenschap?
Wat valt buiten de wetenschap?  Wat zijn de rollen van chlorofyl A & B?
Wat zijn de rollen van chlorofyl A & B?  Is methaan oplosbaar in vloeibare stikstof?
Is methaan oplosbaar in vloeibare stikstof?  Blauwe wijn? Een vintage met thee? Startup Spanje schudt de boel wakker
Blauwe wijn? Een vintage met thee? Startup Spanje schudt de boel wakker Milieu-effecten van de atoombom
Milieu-effecten van de atoombom  Onderzoekers identificeren nieuwe cybersecurity-aanpak om legersystemen te beschermen
Onderzoekers identificeren nieuwe cybersecurity-aanpak om legersystemen te beschermen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

