
Wetenschap
Wat is de verjaardagsparadox?
De waarschijnlijkheid berekenen
Om de waarschijnlijkheid te berekenen dat twee of meer mensen dezelfde verjaardag delen in een groep van n mensen, kunnen we de volgende formule gebruiken:
$$P(minstens\ één\ gedeelde\ verjaardag) =1 - P(geen\ gedeelde\ verjaardagen)$$
waar:
- \(P(minstens\ één\ gedeelde\ verjaardag)\) is de kans dat ten minste twee mensen in de groep dezelfde verjaardag delen.
- \(P(geen\ gedeelde\ verjaardagen)\) is de kans dat geen twee mensen in de groep dezelfde verjaardag delen.
Om \(P(no\ shared\ birthdays)\) te berekenen, kunnen we de volgende formule gebruiken:
$$P(geen\ gedeelde\ verjaardagen) =\frac{365!}{365^n \cdot (365-n)!}$$
waar:
- \(365\) is het aantal dagen in een jaar.
- \(n\) is het aantal mensen in de groep.
Als we bijvoorbeeld een groep van 23 mensen hebben, is de kans dat twee of meer mensen dezelfde verjaardag delen:
$$P(minstens\ één\ gedeelde\ verjaardag) =1 - P(geen\ gedeelde\ verjaardagen)$$
$$=1 - \frac{365!}{365^{23} \cdot (365-23)!}$$
$$=1 - 0,4927=0,5073$$
Daarom is de kans dat twee of meer mensen dezelfde verjaardag delen in een groep van 23 of meer mensen meer dan 50%.
Het verrassingselement
De verjaardagsparadox wordt vaak aangehaald als voorbeeld van een contra-intuïtief waarschijnlijkheidsverschijnsel, en kan worden gebruikt om het belang te illustreren van het begrijpen van de onderliggende wiskunde voordat conclusies uit gegevens worden getrokken. Het belicht ook de verrassende manieren waarop schijnbaar ongerelateerde gebeurtenissen met elkaar in verband kunnen worden gebracht.
 Er worden nieuwe biologisch afbreekbare polyurethaanschuimen ontwikkeld van tarwestro
Er worden nieuwe biologisch afbreekbare polyurethaanschuimen ontwikkeld van tarwestro Hoe gevaarlijk is natuurbrandrook? Een toxicoloog die rode vlaggen opsteekt
Hoe gevaarlijk is natuurbrandrook? Een toxicoloog die rode vlaggen opsteekt  Hoe Agent Orange werkte
Hoe Agent Orange werkte  Groene waterstof:roest als fotoanode en zijn grenzen
Groene waterstof:roest als fotoanode en zijn grenzen Wetenschappers zorgen voor metingen met hoge resolutie voor koolstofdiplomatie
Wetenschappers zorgen voor metingen met hoge resolutie voor koolstofdiplomatie
 Wintertarwe haalbaar dekgewas voor Rolling Plains-katoen
Wintertarwe haalbaar dekgewas voor Rolling Plains-katoen NASA toont winden die de ondergang van tropische cycloon Lornas veroorzaken
NASA toont winden die de ondergang van tropische cycloon Lornas veroorzaken Nieuwe website toont impact Europese virusbeperking
Nieuwe website toont impact Europese virusbeperking Cyclone Feiten voor kinderen
Cyclone Feiten voor kinderen Muziekfestivals worden steeds meer getroffen door de klimaatverandering. Doet de industrie genoeg om de impact te verzachten?
Muziekfestivals worden steeds meer getroffen door de klimaatverandering. Doet de industrie genoeg om de impact te verzachten?
Hoofdlijnen
- Genetische aanwijzingen over hoe honden de beste vrienden van de mens werden
- Regenboogkleuren onthullen celgeschiedenis
- Motoreiwitten vervoeren kostbare lading in neuronen. Hoe kunnen we hun beweging controleren?
- Wat gebeurt er als er geen zuurstof beschikbaar is aan het einde van langzame glycolyse?
- Hoe internationaal toerisme en reizen een manier kunnen zijn om invasieve soorten te introduceren
- Laboratoriumexperimenten met hoge resolutie laten zien hoe cellen 'eten'
- Terwijl de vogelgriep zich verspreidt naar melkkoeien, vertonen de roofvogels van Minnesota tekenen dat ze een opmerkelijke immuniteit opbouwen
- Een heroverweging van ziekten in het licht van fasescheiding en faseovergang kan noodzakelijk zijn
- Van gist naar hypha:hoe Candida albicans de overstap maakt
- Zonnestormvoorspellingen voor de aarde verbeterd met hulp van het publiek
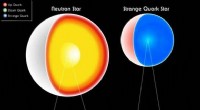
- Is er een manier om vreemde quarksterren te detecteren, ook al zien ze eruit als witte dwergen?
- Breed beeld van vroege heelal hints naar sterrenstelsel onder vroegst gedetecteerde

- TESS dateert een oude botsing met onze melkweg

- Emiraten bereikt als eerste Arabier ISS

 Viagra Hoe werkt
Viagra Hoe werkt  Wetenschappers maken nanotrampoline om kwantumgedrag te onderzoeken
Wetenschappers maken nanotrampoline om kwantumgedrag te onderzoeken Satelliet vindt zuidelijke windschering die de tropische depressie Jelawat . beïnvloedt
Satelliet vindt zuidelijke windschering die de tropische depressie Jelawat . beïnvloedt Nieuwe, op theorie gebaseerde evaluatie geeft een duidelijker beeld van kernfusie in de zon
Nieuwe, op theorie gebaseerde evaluatie geeft een duidelijker beeld van kernfusie in de zon  Kunnen we de kikkerpandemie genezen?
Kunnen we de kikkerpandemie genezen? PAL:een draagbaar systeem voor contextbewuste ondersteuning van gezondheid en cognitie
PAL:een draagbaar systeem voor contextbewuste ondersteuning van gezondheid en cognitie De compromissen die inherent zijn aan vroegtijdige waarschuwingssystemen voor aardbevingen
De compromissen die inherent zijn aan vroegtijdige waarschuwingssystemen voor aardbevingen Onderzoekers ontdekken hoe stamcellen hun identiteit kiezen
Onderzoekers ontdekken hoe stamcellen hun identiteit kiezen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

