
Wetenschap
Als de straal ongeveer 6375 km is, hoe snel moet een satelliet in beweging zijn als deze net boven het oppervlak een rondbeurt met centripetale versnelling van 9,8 ms22?
Inzicht in de concepten
* Centripetale versnelling: De versnelling die nodig is om een object in een cirkelvormig pad te houden. Het is gericht naar het midden van de cirkel.
* zwaartekracht: De aantrekkingskracht tussen twee objecten met massa. In dit geval is het de kracht tussen de aarde en de satelliet.
* Orbitale snelheid: De snelheid waarmee een object moet reizen om een stabiele baan rond een ander object te behouden.
formule
De centripetale versnelling (a) van een object in circulaire beweging wordt gegeven door:
a =v²/r
waar:
* a =centripetale versnelling (9,8 m/s²)
* v =orbitale snelheid (wat we willen vinden)
* r =straal van de baan (6375 km + een kleine hoeveelheid voor "net boven" het oppervlak, laten we zeggen 6378 km =6.378.000 m)
Oplossen voor de orbitale snelheid
1. herschik de formule om op te lossen voor V:
v =√ (a * r)
2. Sluit de waarden aan:
v =√ (9,8 m/s² * 6,378.000 m)
3. Bereken het resultaat:
v ≈ 7905 m/s
converteren naar km/h:
* 7905 m / s * (3600 s / 1 uur) * (1 km / 1000 m) ≈ 28,458 km / h
Daarom moet een satelliet die net boven het aardoppervlak draait om ongeveer 7905 m/s of 28,458 km/u te bewegen om een stabiele baan te behouden.
Belangrijke opmerking: Deze berekening veronderstelt een perfect cirkelvormige baan en verwaarloost luchtweerstand, die de werkelijke snelheid die nodig is voor een satelliet in de echte wereld aanzienlijk zou beïnvloeden.
 Voedselketen met drie organismen die Humans
Voedselketen met drie organismen die Humans Geoloog helpt de datum van vroegste landplanten op aarde te bevestigen
Geoloog helpt de datum van vroegste landplanten op aarde te bevestigen Na de dood van een kind weegt Californië de regels voor lichamelijke opvoeding tijdens extreem weer af
Na de dood van een kind weegt Californië de regels voor lichamelijke opvoeding tijdens extreem weer af  Hoe een dode vlinder te behouden
Hoe een dode vlinder te behouden  Studie toont Witte Huis, Pentagon zijn letterlijk enkele van de populairste plekken in Washington
Studie toont Witte Huis, Pentagon zijn letterlijk enkele van de populairste plekken in Washington
Hoofdlijnen
- Welke cel kan een benige matrix opbouwen?
- Lichaamsdelen en functies
- Onderscheid maken tussen eencellige en meercellige organismen?
- Is de volgende vraag waar of onwaar classificeren, maakt het gemakkelijker om organismen te vergelijken en te contrasteren hun actiesgedragfuncties?
- Welk wetenschappelijk woord begint met Z?
- Wat is een cel met complexe membraangebonden organellen genoemd?
- Hoe jonge oesters de metamorfose van vleesetende buikpotige Rapana venosa beïnvloeden
- Waar bevinden hydro -bindingen zich in de DNA -streng?
- Welke kenmerken onderscheiden schimmels van planten?
- 3D-kwantumgas-atoomklok biedt nieuwe dimensies in meten

- Een wereldrecord in het detecteren van extreem lage niveaus van gasonzuiverheden
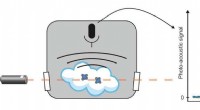
- Kosmische theoreticus en planeetjagers delen natuurkundeprijs terwijl Nobels buitenaardse ontdekkingen belonen

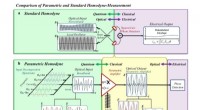
- Een kwantumsprong maken in kwantumcommunicatie
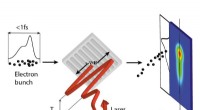
- Lasers gebruiken om ultrakorte pulsen te creëren
 Wat kunnen we leren van de natuurkunde?
Wat kunnen we leren van de natuurkunde?  Hoe Crusher werkt
Hoe Crusher werkt  Wat is een rigide laag die bestaat uit het bovenste deel mantel en korst?
Wat is een rigide laag die bestaat uit het bovenste deel mantel en korst?  Kaketoe-ontdekking onthult bloeiende middeleeuwse handelsroutes rond het noorden van Australië
Kaketoe-ontdekking onthult bloeiende middeleeuwse handelsroutes rond het noorden van Australië Streamen naar abonnementen:videogames betreden nieuwe grenzen
Streamen naar abonnementen:videogames betreden nieuwe grenzen Wat waren de sociale economische en milieueffecten van 79 ad -uitbarsting Mount Vesuvius?
Wat waren de sociale economische en milieueffecten van 79 ad -uitbarsting Mount Vesuvius?  Nieuwe theorie over het ontstaan van de asteroïdengordel
Nieuwe theorie over het ontstaan van de asteroïdengordel Onderzoekers onthullen unieke getijdenverstoring met uitgesproken vroege optische hobbel
Onderzoekers onthullen unieke getijdenverstoring met uitgesproken vroege optische hobbel
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

