
Wetenschap
Twee objecten trekken elkaar zwaartekracht aan met een kracht van 2,5x10-10 N wanneer ze 25 meter uit elkaar liggen, hun totale massa is 4,0 kg Vind hun individuele massa?
1. Begrijp de concepten
* Newton's Law of Universal Gravitation: De zwaartekracht tussen twee objecten is recht evenredig met het product van hun massa en omgekeerd evenredig met het kwadraat van de afstand tussen hun centra. De vergelijking is:
F =g * (m1 * m2) / r²
Waar:
* F is de zwaartekracht
* G is de zwaartekrachtconstante (6.674 × 10⁻¹¹ N⋅m²/kg²)
* M1 en M2 zijn de massa van de objecten
* r is de afstand tussen hun centra
* Totale massa: De som van de individuele massa's van de twee objecten.
2. Stel de vergelijkingen in
We hebben twee onbekenden (M1 en M2) en twee vergelijkingen die we kunnen gebruiken:
* Vergelijking 1 (zwaartekracht): 2.5 × 10⁻¹⁰ n =g * (m1 * m2) / (25 m) ²
* Vergelijking 2 (totale massa): M1 + M2 =4,0 kg
3. Oplossen voor de massa
* Los voor de ene massa in termen van de andere:
* Uit vergelijking 2 krijgen we:M1 =4,0 kg - M2
* Vervang dit in vergelijking 1:
* 2.5 × 10⁻¹⁰ n =g * ((4,0 kg - m2) * m2) / (25 m) ²
* Vereenvoudig en oplossen voor M2:
* 2.5 × 10⁻¹⁰ n * (25 m) ² =g * (4,0 kg * m2 - m2²)
* 1.5625 × 10⁻⁶ =(6.674 × 10⁻¹¹ n⋅m²/kg²) * (4,0 kg * m2 - m2²)
* 23400 =4.0 * M2 - M2²
* M2² - 4.0 * M2 + 23400 =0
* Gebruik de kwadratische formule om op te lossen voor M2:
* m2 =(-b ± √ (b² - 4ac)) / 2a
* Waar a =1, b =-4 en c =23400
* Dit geeft u twee mogelijke waarden voor M2. De ene zal een realistische massa zijn en de andere zal erg groot en onrealistisch zijn.
* Zoek m1:
* Zodra u M2 hebt, sluit u het terug op Vergelijking 1 of Vergelijking 2 om op te lossen voor M1.
Laat het me weten als je hulp nodig hebt bij het oplossen van de kwadratische vergelijking om de uiteindelijke waarden voor M1 en M2 te krijgen.
Hoofdlijnen
- De aarde herbergt 20.000.000.000.000.000 mieren. En ze wegen meer dan wilde vogels en zoogdieren samen
- Waarom planten spruiten vormen in het donker
- Wat bestaat uit DNA en eiwitten?
- Nieuwe methode zou kunnen onthullen welke genen van Neanderthalers zijn geërfd
- Hoe wijzen de bevindingen op micro -evolutie maar geen macro -evolutie?
- Hoe gebruiken cellen diffusie en osmose?
- Protisten die een multinucleate glob met cytoplasma produceren, is?
- Welk molecuul bevat de informatie over het maken van eiwitten?
- Wat is bacterialisme?
- De symmetrie van ruimte-tijd testen door middel van atoomklokken

- Aan de hand van de natuur, baanbrekende technologie voor cellulaire fluïdica kan ingrijpende gevolgen hebben

- Vloeistofinterface-ondersteunde SERS zouden de ziekte van Alzheimer eerder kunnen detecteren
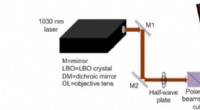
- Laser- en sensoronderzoek moet worden bevorderd door nieuwe onderzoeken naar plasmonisch-fotonische kristallen

- Nieuw paradigma voor het automatisch afstemmen van kwantumbits kan een grote technische hindernis overwinnen
 Wie zijn wetenschapper die de cel ontdekken?
Wie zijn wetenschapper die de cel ontdekken?  Quantum dots bieden volledige controle over fotonen
Quantum dots bieden volledige controle over fotonen Wat ontstond er als eerste:een behendige hand of een behendige voet?
Wat ontstond er als eerste:een behendige hand of een behendige voet?  Natuurkundigen onthulden spontane T-symmetrie breuken en uitzonderlijke punten in holte QED
Natuurkundigen onthulden spontane T-symmetrie breuken en uitzonderlijke punten in holte QED De Filippijnse bioloog en hun bijdragen?
De Filippijnse bioloog en hun bijdragen?  Onderzoekers ontdekken hoe gelei-zeedieren moderne robotica kunnen vormen
Onderzoekers ontdekken hoe gelei-zeedieren moderne robotica kunnen vormen  Mijnwerkers schakelen over op bijenteelt
Mijnwerkers schakelen over op bijenteelt Chemici synthetiseren ultrasnelle cyanidedetector
Chemici synthetiseren ultrasnelle cyanidedetector
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com


