
Wetenschap
Wat zijn verschillende methoden om het resultaat van twee krachten te berekenen?
Inzicht in het concept
* Force: Een duw of trek die een verandering in de beweging van een object kan veroorzaken.
* resulterende kracht: De enkele kracht die hetzelfde effect produceert als twee of meer krachten die samen werken.
methoden om de resulterende kracht te berekenen
1. grafische methode (parallellogramwet):
* Visuele weergave: Deze methode gebruikt een schaaltekening om de resulterende kracht te vinden.
* stappen:
1. Teken: Teken de twee krachten (vectoren) op schaal, beginnend bij hetzelfde punt (staart tot staart).
2. Voltooi het parallellogram: Construeer een parallellogram met behulp van de twee krachten als aangrenzende zijden.
3. Diagonaal: De diagonaal van het parallellogram, getrokken uit het gemeenschappelijke uitgangspunt, vertegenwoordigt de resulterende kracht.
4. Meet: Meet de lengte en richting van de diagonaal om de grootte en richting van de resulterende kracht te bepalen.
2. Analytische methode (trigonometrie):
* Wiskundige aanpak: Deze methode maakt gebruik van trigonometrie om de resulterende kracht te berekenen.
* stappen:
1. Los krachten op: Breek elke kracht af in zijn horizontale (X-component) en verticale (Y-component) componenten.
2. Somcomponenten: Voeg de X-componenten en Y-componenten van de twee krachten afzonderlijk toe.
3. Vind magnitude: Bereken de grootte van de resulterende kracht met behulp van de stelling van Pythagoras:
* Resulterende kracht (r) =√ ((σfx) ² + (σfy) ²)
4. Richting vinden: Bereken de hoek (θ) van de resulterende kracht ten opzichte van een referentieas (vaak de horizontale) met behulp van de arctangente functie:
* θ =arctan (σfy / σfx)
3. Vector toevoeging:
* Vectorrepresentatie: Deze methode maakt gebruik van vectornotatie (grootte en richting) om krachten weer te geven.
* stappen:
1. Krachten uitdrukken: Vertegenwoordigen elke kracht als een vector (bijv. F1 =(x1, y1), f2 =(x2, y2)).
2. Voeg componenten toe: Voeg de overeenkomstige componenten van de vectoren toe:
* Resulterende kracht (r) =(x1 + x2, y1 + y2)
3. Grootte en richting: Bereken de grootte en richting van de resulterende kracht met behulp van de methoden die zijn beschreven in de analytische methode.
voorbeelden
Voorbeeld 1:grafische methode
Stel je twee krachten voor die op een object handelen:
* F1 =10 N, 30 ° boven de horizontale
* F2 =5 n, 60 ° onder de horizontale
Met behulp van de parallellogramwet zou u een diagram trekken om op te schalen en de diagonaal te vinden die de resulterende kracht vertegenwoordigt.
Voorbeeld 2:analytische methode
* F1 =(5 n, 0 °) (5 n horizontaal rechts)
* F2 =(0 n, 3 n) (3 n verticaal omhoog)
1. Resolve: Geen behoefte aan resolutie hier.
2. Somcomponenten: Σfx =5 n, σfy =3 n
3. magnitude: R =√ (5² + 3²) =√34 ≈ 5.83 n
4. richting: θ =arctan (3/5) ≈ 30,96 ° (boven de horizontale)
belangrijke punten:
* eenheden: Zorg ervoor dat alle krachten in dezelfde eenheden worden uitgedrukt (bijv. Newton).
* richting: Overweeg altijd de richting van de krachten bij het berekenen van de resulterende kracht.
* Vector toevoeging: Vector -toevoeging volgt dezelfde principes als de analytische methode, maar het is beknopter met behulp van vectornotatie.
Laat het me weten als je specifieke voorbeelden of scenario's hebt die je wilt doorwerken!
 Nieuw-Zeeland investeert in de groei van zijn binnenlandse recyclingindustrie om banen te creëren en minder afval op stortplaatsen te dumpen
Nieuw-Zeeland investeert in de groei van zijn binnenlandse recyclingindustrie om banen te creëren en minder afval op stortplaatsen te dumpen Hoe kun je dierenpaden identificeren in sneeuw
Hoe kun je dierenpaden identificeren in sneeuw Onderzoek zegt dat steden in India rekening moeten houden met extreme regenval bij het plannen van nieuwe infrastructuur
Onderzoek zegt dat steden in India rekening moeten houden met extreme regenval bij het plannen van nieuwe infrastructuur Vraag en antwoord:Gasachtige koeien, lekkende putten en andere avonturen bij het meten van methaan
Vraag en antwoord:Gasachtige koeien, lekkende putten en andere avonturen bij het meten van methaan Hoe kwamen veranderende ideeën over de rol van individuele invloeden op de manier waarop wetenschappers de fysieke wereld begonnen te begrijpen?
Hoe kwamen veranderende ideeën over de rol van individuele invloeden op de manier waarop wetenschappers de fysieke wereld begonnen te begrijpen?
Hoofdlijnen
- Welke vier dingen doen levende wezens?
- Wat is neurale modulariteit?
- Cultuur kan verklaren waarom hersenen groter zijn geworden
- Centriolen:je kunt cellen niet verdelen zonder ze
- Wat is bindweefsel en vermeldt u de belangrijkste soorten in het menselijk lichaam?
- Scheidingswanden:hoe immuuncellen weefsel binnendringen
- Waarom laten mensen twee sets tanden groeien? Deze buideldieren herschrijven het verhaal van tandheelkundige evolutie
- Wat gebeurt er met een enzym als de temperatuur te ver van de optimale temperatuur van enzymen varieert?
- Wat betekenen gegevens in het wetenschapsproject?
- Experiment onthult nieuwe opties voor synchrotron-lichtbronnen

- Waar halen ze de deeltjes voor versnellers?

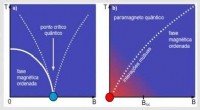
- Theoretisch onderzoek toont aan dat materie de neiging heeft om bij lage temperaturen te worden geordend
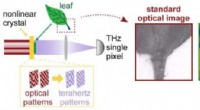
- Onderzoekers combineren lasers en terahertz-golven in een camera die ongeziene details ziet
- Onderzoekers schenden Bells-ongelijkheid met op afstand verbonden supergeleidende qubits

 Hebben we Peak Car bereikt?
Hebben we Peak Car bereikt? Kan de grote Hadron Collider de aarde vernietigen?
Kan de grote Hadron Collider de aarde vernietigen?  Dagelijkse voorbeelden van prisma's
Dagelijkse voorbeelden van prisma's  Onderzoeksteam buigt individuele tetrapod nanostructuren
Onderzoeksteam buigt individuele tetrapod nanostructuren Wat voor soort rots zou je op de top een berg vinden?
Wat voor soort rots zou je op de top een berg vinden?  Een object weegt 120n op aarde, wat zal het gewicht van de maan zijn?
Een object weegt 120n op aarde, wat zal het gewicht van de maan zijn?  Wanneer was de laatste uitbarsting van Pilot Knob?
Wanneer was de laatste uitbarsting van Pilot Knob?  Een hexagon
Een hexagon
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

