
Wetenschap
Een bal van massa M is vastgebonden aan een touwtje die rond de buitenpoelie wordt gewikkeld. De poelie welke uniforme vaste schijf ook heeft en roteert zonder wrijving over Axle T?
Inzicht in de setup
* bal: Een massa 'm' verticaal hangt.
* string: Een lichte snaar die de bal met de poelie verbindt, aangenomen massaal en uitextenbaar.
* poelie: Een uniforme vaste schijf met een moment van traagheid (I) en een straal (R).
* Wrijvingsloze as: De poelie draait vrij zonder wrijvingsverliezen.
Key Concepts
* Conservering van energie: De totale mechanische energie van het systeem (bal en poelie) blijft constant. Dit betekent de som van potentiële energie, kinetische energie van de bal en rotatiekinetische energie van de poelie constant.
* rotatiebeweging: De poelie ervaart hoekversnelling als gevolg van het koppel dat wordt geproduceerd door de spanning in de string.
* koppel: De spanning in de string creëert een koppel op de poelie, waardoor deze roteert.
* Traagheidsmoment: Een maat voor hoe resistent een object is om veranderingen in zijn rotatiebeweging te veranderen. Voor een vaste schijf, I =(1/2) mr².
De vergelijkingen afleiden
1. Krachten handelen op de bal:
* Gravity:Mg (naar beneden)
* Spanning in de string:t (omhoog)
2. Forces handelen op de poelie:
* Spanning in de string:t (tangentiële kracht)
3. bewegingsvergelijkingen voor de bal:
* Newton's tweede wet:ma =mg - t
* Versnelling van de bal:a =(g - t/m)
4. bewegingsvergelijkingen voor de poelie:
* Koppel:τ =tr
* Angulaire versnelling:α =τ/i =(tr)/(1/2Mr²) =(2t/mr)
* Relatie tussen lineaire versnelling (a) en hoekversnelling (α):a =ra
5. Behoud van energie:
* Initiële potentiële energie van de bal:mgh (waar 'h' de eerste hoogte is)
* Uiteindelijke potentiële energie van de bal:0 (wanneer de bal de bodem bereikt)
* Kinetische energie van de bal:(1/2) mv²
* Rotatiekinetische energie van de poelie:(1/2) iω² =(1/4) mr²ω²
6. met betrekking tot lineaire en hoeksnelheden:
* v =rω
Het probleem oplossen
1. Oplossen voor spanning (t):
* Vervang de uitdrukking voor 'a' uit de bewegingsvergelijking van de bal in de relatie tussen lineaire en hoekige versnelling (a =ra).
* Je zult dat t =(2/3) mg vinden
2. Vind de versnelling (a):
* Vervang de waarde van T in de bewegingsvergelijking van de bal (Ma =mg - t).
* Je krijgt a =(1/3) g
3. Bereken de hoekversnelling (α):
* Gebruik de vergelijking α =(2T/MR) en vervang de waarde van T.
4. Bepaal de snelheid (V) van de bal:
* Gebruik het behoud van energievergelijking en lost op voor 'V'.
Key Points
* De spanning in de string is minder dan het gewicht van de bal als gevolg van de rotatie -traagheid van de poelie.
* De versnelling van de bal is minder dan 'G' omdat de rotatie van de poelie het vertraagt.
* De energie die door de bal wordt verloren terwijl deze valt, wordt overgebracht naar de rotatiekinetische energie van de poelie.
Laat het me weten als u een specifieke vraag hebt of een van deze waarden wilt berekenen. Ik kan indien nodig meer gedetailleerde berekeningen bieden.
 NASA-NOAA-satelliet ziet aan land vallende orkaan Florence
NASA-NOAA-satelliet ziet aan land vallende orkaan Florence Welke laag is heter dan het oppervlak van de zon?
Welke laag is heter dan het oppervlak van de zon?  Warmte, vochtigheid houdt het oosten van de VS vast terwijl het weekend ploetert
Warmte, vochtigheid houdt het oosten van de VS vast terwijl het weekend ploetert Een nieuwe golf van slimme steden is gearriveerd - en ze lijken in niets op sciencefiction
Een nieuwe golf van slimme steden is gearriveerd - en ze lijken in niets op sciencefiction Wetenschappers stellen voor om de regels van de geschiedenis te veranderen om de ineenstorting van het milieu te voorkomen
Wetenschappers stellen voor om de regels van de geschiedenis te veranderen om de ineenstorting van het milieu te voorkomen
Hoofdlijnen
- Wat is een veronderstelde ontwikkeling van het leven van de gewone voorouder?
- Snelle evolutie:Aanhoudende snelle evolutie verklaart hoe tetrapoden uit vissen evolueerden
- Wat zijn de rollen van chlorofyl A & B?
- Waarom is water naar levende organismen?
- Langdurige relatie met eigenaar vermindert stressreacties van paarden in nieuwe situaties
- Welke stikstofbasis is uniek voor RNA -moleculen?
- Een wortel is een voorbeeld van een?
- Wat is een eigenschap die niet tot expressie wordt gebracht wanneer een organisme genen ontvangt voor 2 verschillende vormen van eigenschap?
- Waarom falen de besturen van sommige organisaties? Het kan zijn hoe bestuurders hun expertise en verantwoordelijkheden waarnemen
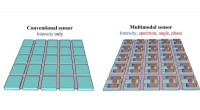
- Beeldsensoren verbeteren voor machine vision
- Precisiemeting van zware ionen is in tegenspraak met de theorie van interactie tussen atoomkern en elektron

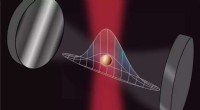
- Microholten als sensorplatform
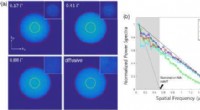
- Verbetering van diepe optische microscoopbeeldvorming van biologische weefsels
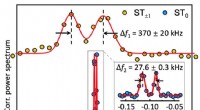
- Single-spin elektron paramagnetisch resonantiespectrum met kilohertz spectrale resolutie
 Wat zijn de verschillen in klimaat aan de Leeward -kant van een berg- en windwaartse kant?
Wat zijn de verschillen in klimaat aan de Leeward -kant van een berg- en windwaartse kant?  Seychellen-chef roept vanuit de diepte voor bescherming van de oceaan
Seychellen-chef roept vanuit de diepte voor bescherming van de oceaan Wat gebeurt er als Benzeen reageert met CH3COCL in aanwezigheid OA Hydrous Alcl3?
Wat gebeurt er als Benzeen reageert met CH3COCL in aanwezigheid OA Hydrous Alcl3?  Facebook scherpt regels voor politieke advertenties aan in aanloop naar Amerikaanse verkiezingen
Facebook scherpt regels voor politieke advertenties aan in aanloop naar Amerikaanse verkiezingen Hoe beïnvloedt concurrentie met andere planten de groei van planten?
Hoe beïnvloedt concurrentie met andere planten de groei van planten?  Waar komt de thermionische emissie op in de kathodestralen?
Waar komt de thermionische emissie op in de kathodestralen?  Hoeveel energie geeft de zon van?
Hoeveel energie geeft de zon van?  Je bent een grote massa bevroren water, je kunt rotsen en keien heel langzaam verplaatsen, maar geweldige kamers op aarde veroorzaken wat je?
Je bent een grote massa bevroren water, je kunt rotsen en keien heel langzaam verplaatsen, maar geweldige kamers op aarde veroorzaken wat je?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

