
Wetenschap
Wat is het traagheidsmoment voor discreet systeem?
Hier is de formule:
i =σ (mᵢ * rᵢ²)
Waar:
* i is het moment van traagheid
* Mᵢ is de massa van het I-de deeltje
* rᵢ is de afstand van het I-de deeltje van de rotatieas
* σ vertegenwoordigt de sommatie over alle deeltjes in het systeem
Laten we het afbreken:
* Moment van traagheid is een maat voor de weerstand van een object tegen rotatiebeweging. Het is net als het rotatie -equivalent van massa.
* Discreet systeem: Dit verwijst naar een systeem dat bestaat uit afzonderlijke, individuele deeltjes.
Voorbeeld:
Stel je drie deeltjes voor met massa's van 1 kg, 2 kg en 3 kg, gelegen op afstanden van respectievelijk 1 meter, 2 meter en 3 meter vanaf een rotatieas. Om het traagheidsmoment van dit systeem te vinden:
1. Bereken het product van massa en afstand in het kwadraat voor elk deeltje:
- deeltje 1:1 kg * (1 m) ² =1 kg * m²
- Deeltiek 2:2 kg * (2 m) ² =8 kg * m²
- Deeltiek 3:3 kg * (3 m) ² =27 kg * m²
2. Som deze waarden:
- i =1 kg*m² + 8 kg*m² + 27 kg*m² =36 kg*m²
Daarom is het traagheidsmoment van dit discrete systeem 36 kg*m².
Belangrijke punten om te onthouden:
* Het traagheidsmoment hangt af van de massaverdeling in het systeem en de rotatieas.
* De eenheden van het traagheidsmoment zijn kg* m² (kilogram-meter kwadraat).
* De formule voor een discreet systeem is van toepassing op een willekeurig aantal deeltjes.
Dit concept is fundamenteel in het begrijpen van rotatiebeweging, omdat het helpt bij het bepalen van de hoekversnelling van een object onder een bepaald koppel.
 Bescherming van natriummetaalanoden ontmoet in situ foto-elektronenspectroscopie
Bescherming van natriummetaalanoden ontmoet in situ foto-elektronenspectroscopie Een solide weg naar waterstofopslag
Een solide weg naar waterstofopslag Wat is het wetenschappelijke proces dat ervoor zorgt dat het waterpeil daalt als het warmer wordt?
Wat is het wetenschappelijke proces dat ervoor zorgt dat het waterpeil daalt als het warmer wordt?  Waar is een Ant-Atueel van gemaakt?
Waar is een Ant-Atueel van gemaakt?  Veel oude boeken bevatten giftige chemicaliën. Zo kun je ze herkennen
Veel oude boeken bevatten giftige chemicaliën. Zo kun je ze herkennen
 Water beweegt langs het grondoppervlak. Hoe heet dat?
Water beweegt langs het grondoppervlak. Hoe heet dat?  Welke effecten kunnen concurrentie voor hulpbronnen hebben over de verdelingen van plantensoorten?
Welke effecten kunnen concurrentie voor hulpbronnen hebben over de verdelingen van plantensoorten?  Oh, wat had jij grote tanden! Uitgestorven soorten hadden een groot gehemelte
Oh, wat had jij grote tanden! Uitgestorven soorten hadden een groot gehemelte  Oude Maya-steden waren gevaarlijk verontreinigd met kwik
Oude Maya-steden waren gevaarlijk verontreinigd met kwik Waarom steeds meer koppels ervoor kiezen om apart te gaan wonen
Waarom steeds meer koppels ervoor kiezen om apart te gaan wonen
Hoofdlijnen
- Wat was het experiment van Louis Pasteur op biogenese?
- Wie publiceerde de Philosophaiae Naturalis Principia Mathematica?
- Wat zijn de niveaus van biologische classificatie van grootste groepering tot kleinste groepering?
- Uit onderzoek blijkt hoe gemakkelijk het is om iemands identiteit vast te stellen met mobiele telefoongegevens
- Controle van celpopulatiegroottes:wanneer is genoeg genoeg?
- Welke rollen spelen modellenwetten en theorieën in de wetenschap?
- Verband tussen nummervolgorde en ritmische timing bij zangvogels
- Wat zijn de vier steriele sites in het menselijk lichaam?
- Geef aan voor welk voedsel wordt gebruikt door het lichaam?
- Optische gegevensverwerking profiteert van nieuw soort mobiliteit
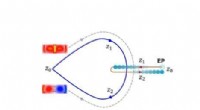
- Reflecterende antiferromagnetische arrangementen
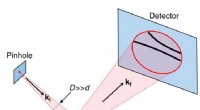
- Een vereenvoudigde methode voor het kalibreren van optische pincetten

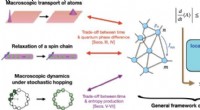
- Snelheidslimieten voor kwantumverschijnselen zijn uitgebreid tot objecten van macroformaat
- Het hipster-effect:waarom anti-conformisten er altijd hetzelfde uitzien

 Wat was de naam van ruimtevaartuigen die de maan bezocht?
Wat was de naam van ruimtevaartuigen die de maan bezocht?  Waarom heeft Violet Light meer energie dan een rood licht?
Waarom heeft Violet Light meer energie dan een rood licht?  E-mails tonen de Vista-problemen van Microsoft
E-mails tonen de Vista-problemen van Microsoft  Steden met meer zwarte inwoners zijn meer afhankelijk van verkeersboetes en boetes voor inkomsten
Steden met meer zwarte inwoners zijn meer afhankelijk van verkeersboetes en boetes voor inkomsten Wat gebeurt er als de snelheid rond de zon afneemt of toeneemt?
Wat gebeurt er als de snelheid rond de zon afneemt of toeneemt?  Decontaminatie van water met zware metalen met behulp van eiwit uit plantaardig afval
Decontaminatie van water met zware metalen met behulp van eiwit uit plantaardig afval De Top 10 Oorzaken van Global Warming
De Top 10 Oorzaken van Global Warming  Hoe verschillen continentale klimaten van gematigde klimaten?
Hoe verschillen continentale klimaten van gematigde klimaten?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

