
Wetenschap
Hoe beïnvloedt massa het hoekmomentum?
hoekmomentumformule:
Angular Momentum (L) wordt berekend met behulp van de volgende formule:
l =iω
waar:
* l is hoekmomentum
* i is het moment van traagheid
* ω is de hoeksnelheid
Moment van traagheid en massa:
Het traagheidsmoment (i) is een maat voor de weerstand van een object tegen veranderingen in de rotatie. Het hangt af van:
* massa (m): Hoe groter de massa, hoe groter het traagheidsmoment. Dit betekent dat een zwaarder object moeilijker te roteren zal zijn.
* Verdeling van massa: Hoe de massa wordt verdeeld rond de rotatieas beïnvloedt ook het traagheidsmoment. Een massa die verder van de rotatieas is geconcentreerd, zal een hoger traagheidsmoment hebben dan een massa geconcentreerd dichter bij de as.
Relatie met hoekmomentum:
Omdat het traagheidsmoment (I) recht evenredig is met massa (M), is Angular Momentum (L) ook recht evenredig met massa. Dit betekent:
* toenemende massa verhoogt het hoekmomentum: Als u de massa van een object verhoogt terwijl u zijn hoeksnelheid houdt en hetzelfde vormt, zal het hoekmomentum evenredig toenemen.
* Afnemende massa vermindert het hoekmomentum: Omgekeerd zal het verminderen van de massa van een object zijn hoekmomentum verminderen.
Voorbeeld:
Stel je een draaiende schaatser voor. Wanneer ze hun armen dicht bij hun lichaam trekken, verminderen ze in wezen de massaverdeling rond de rotatieas. Dit verlaagt hun traagheidsmoment. Om een hoekmomentum te behouden, neemt hun hoeksnelheid (draaiende snelheid) toe. Het totale hoekmomentum van de skater blijft hetzelfde, maar de massaverdelingsverandering heeft het evenwicht tussen traagheidsmoment en hoeksnelheid verschoven.
Samenvattend:
* Massa beïnvloedt direct het hoekmomentum door zijn invloed op het moment van traagheid.
* Grotere massa betekent een groter moment van traagheid, wat op zijn beurt leidt tot een hoger hoekmomentum voor dezelfde hoeksnelheid.
* Veranderingen in massadistributie kunnen het hoekmomentum veranderen, zelfs als de totale massa hetzelfde blijft.
 Wat zijn de producten van stikstoffixatie?
Wat zijn de producten van stikstoffixatie?  Interactie met kernafval in het milieu kan ingewikkelder zijn dan ooit werd gedacht
Interactie met kernafval in het milieu kan ingewikkelder zijn dan ooit werd gedacht Sleutel tot koolstofvrije auto's? Kijk naar de sterren
Sleutel tot koolstofvrije auto's? Kijk naar de sterren Wanneer 2 kleurloze vloeistoffen gemengd Togather om een felgele vaste vaste stof te vormen, welke fysieke eigenschappen zijn veranderd?
Wanneer 2 kleurloze vloeistoffen gemengd Togather om een felgele vaste vaste stof te vormen, welke fysieke eigenschappen zijn veranderd?  Studie is gericht op het stimuleren van de antitumorale activiteit van een verbinding die is geëxtraheerd uit een Amazone-plant
Studie is gericht op het stimuleren van de antitumorale activiteit van een verbinding die is geëxtraheerd uit een Amazone-plant
 Waterkracht in Cambodja kan de voedselzekerheid van de regio bedreigen
Waterkracht in Cambodja kan de voedselzekerheid van de regio bedreigen Waarom zijn fotosynthetische organismen zoals planten zo belangrijk voor het leven op aarde?
Waarom zijn fotosynthetische organismen zoals planten zo belangrijk voor het leven op aarde?  Wat zijn vier niet-levende dingen in een woestijnecosysteem?
Wat zijn vier niet-levende dingen in een woestijnecosysteem?  Verandering van de vorm van valleien en dammen verandert het nitraatniveau van oppervlakte en grondwater op de schaal van het stroomgebied
Verandering van de vorm van valleien en dammen verandert het nitraatniveau van oppervlakte en grondwater op de schaal van het stroomgebied Hoe zijn palmbomen nuttig in de woestijn?
Hoe zijn palmbomen nuttig in de woestijn?
Hoofdlijnen
- Waarom is succinaat dehydrogenase een goed marker -enzym?
- Bijen en vlinders gaan achteruit in westelijk en zuidelijk Noord-Amerika
- Welk deel van het Nephron is verantwoordelijk voor de reabsorptie van water?
- Noem de 4 cellen die door oögenese worden geproduceerd?
- Welk element wordt als het meest veelzijdig beschouwd in levende organismen en waarom?
- Wat is een genclustering?
- Hoe goed worden alternatieve eiwitbronnen ontvangen door de eindconsument?
- Waarom zijn er extra onderdelen in een plantencel?
- Welk celtype is de geleidende cel van het zenuwstelsel?
- Een nucleaire klokovergang onderzoeken

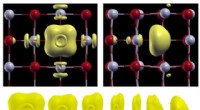
- Nieuwe analyse verklaart rol van defecten in metaaloxiden
- Vastestoffysica biedt inzicht in diëlektrische eigenschappen van biomaterialen

- Nieuwe röntgenoptica verbetert de beeldvormingsmogelijkheden bij NSLS-II

- Waarschuwingssysteem voor defecte leidingen van kerncentrales maakt gebruik van dunne films en geluidstrillingen

 De beweging van aardkorst vormt metamorfe rots wanneer?
De beweging van aardkorst vormt metamorfe rots wanneer?  Wat zijn de specificaties en kwaliteiten voor stikstofzuiverheid?
Wat zijn de specificaties en kwaliteiten voor stikstofzuiverheid?  Neutrino-experimenten lijken grote antwoorden te onthullen over hoe deze fundamentele deeltjes interageren met materie
Neutrino-experimenten lijken grote antwoorden te onthullen over hoe deze fundamentele deeltjes interageren met materie Wilt u weten waar bedreigde soorten leven? Kijk naar de wolken
Wilt u weten waar bedreigde soorten leven? Kijk naar de wolken  Zijn er zwarte gaten ontstaan direct na de oerknal?
Zijn er zwarte gaten ontstaan direct na de oerknal?  Onderzoeksconsortium produceert 3D-kaart met hoge resolutie van GLP-1R
Onderzoeksconsortium produceert 3D-kaart met hoge resolutie van GLP-1R Een mengsel van 0,220 mol CO 0,350 H2 en 0,640 Hij heeft een totale druk van 2,95 Atm, wat is de H2?
Een mengsel van 0,220 mol CO 0,350 H2 en 0,640 Hij heeft een totale druk van 2,95 Atm, wat is de H2?  Nieuwe zonneceltechnologie legt hoogenergetische fotonen efficiënter vast
Nieuwe zonneceltechnologie legt hoogenergetische fotonen efficiënter vast
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

