
Wetenschap
Wat is de snelheid en versnelling van een bal die over de heuvel rolt?
Factoren die de snelheid en versnelling beïnvloeden:
* helling van de heuvel: Een steilere helling resulteert in een hogere versnelling en een hogere uiteindelijke snelheid.
* Initiële snelheid: Als de bal begint met een beginsnelheid, zal de snelheid hoger zijn dan wanneer deze begint bij rust.
* Wrijving: Wrijving tussen de bal en het oppervlak van de heuvel (inclusief luchtweerstand) zal de bal vertragen, waardoor zowel zijn snelheid als versnelling worden verminderd.
* massa van de bal: De massa van de bal heeft geen direct invloed op de versnelling (vanwege de zwaartekracht), maar het heeft wel invloed op hoeveel kracht nodig is om wrijving te overwinnen.
* Vorm en grootte van de bal: Een bal met een groter oppervlak zal meer luchtweerstand ervaren, waardoor het wordt vertraagd.
Berekening van snelheid en versnelling:
Om de snelheid en versnelling van de bal te berekenen, kunt u de volgende bewegingsvergelijkingen gebruiken:
* versnelling (a): Ervan uitgaande dat alleen zwaartekracht op de bal werkt, is de versnelling constant en gelijk aan `g * sin (theta)`, waarbij `g` de versnelling is als gevolg van de zwaartekracht (ongeveer 9,8 m/s²) en` theta 'is de hoek van de helling.
* Eindsnelheid (V): `v² =u² + 2AS`, waarbij` u` de beginsnelheid is, `a` is de versnelling en` s` is de afgelegde afstand.
* tijd (t): `v =u + at`
Voorbeeld:
Laten we aannemen dat een bal begint vanaf rust op de top van een heuvel met een helling van 30 graden.
* versnelling (a): `a =g * sin (theta) =9,8 m/s² * sin (30 °) =4,9 m/s²`
* Eindsnelheid (V): We moeten de afgelegde afstand weten om de uiteindelijke snelheid te berekenen. Als de afstand bijvoorbeeld 10 meter is, dan `v² =0² + 2 * 4,9 m/s² * 10 m =98 m²/s²` en` v =√98 m²/s² =9,9 m/s`.
* tijd (t): Met dezelfde afstand als in het vorige voorbeeld, kunnen we de tijd berekenen die nodig is om de bodem van de heuvel te bereiken:`t =(v - u)/a =(9,9 m/s - 0 m/s)/4,9 m/s² =2.02 s`.
belangrijke opmerkingen:
* Deze vergelijkingen zijn vereenvoudigd en houden geen rekening met factoren zoals wrijving of luchtweerstand.
* De werkelijke snelheid en versnelling van een bal die bergafwaarts rolt, zal iets minder zijn dan wat wordt berekend met behulp van deze vergelijkingen.
Vergeet niet dat dit slechts theoretische berekeningen zijn. In werkelijkheid zal de werkelijke snelheid en versnelling worden beïnvloed door een combinatie van factoren.
 Schoonheid in imperfectie:hoe kristaldefecten kunnen helpen afvalwarmte om te zetten in elektriciteit
Schoonheid in imperfectie:hoe kristaldefecten kunnen helpen afvalwarmte om te zetten in elektriciteit Welke wetenschapper zei dat er verschillende elementen zijn gemaakt van soorten atomen?
Welke wetenschapper zei dat er verschillende elementen zijn gemaakt van soorten atomen?  Welk element op het periodiek systeem is vergelijkbaar met Ununoctium?
Welk element op het periodiek systeem is vergelijkbaar met Ununoctium?  Dagelijks gebruik van Helium Gas
Dagelijks gebruik van Helium Gas Is hexaan een verbinding of mengsel?
Is hexaan een verbinding of mengsel?
 Wetenschappers identificeren potentiële bio-indicatoren voor het monitoren van plasticvervuiling in de noordelijke Stille Oceaan
Wetenschappers identificeren potentiële bio-indicatoren voor het monitoren van plasticvervuiling in de noordelijke Stille Oceaan Australiës Big Wet-gemakken, maar duizenden nog steeds geïsoleerd
Australiës Big Wet-gemakken, maar duizenden nog steeds geïsoleerd Hoe Alang Shipyard werkt
Hoe Alang Shipyard werkt  NASA ziet sterke stormen in tropische depressie 05W naarmate het sterker wordt
NASA ziet sterke stormen in tropische depressie 05W naarmate het sterker wordt Onderzoek suggereert manieren om meer duurzaamheid in de mondiale landbouwhandel te garanderen
Onderzoek suggereert manieren om meer duurzaamheid in de mondiale landbouwhandel te garanderen
Hoofdlijnen
- Wat is de enige levensfunctie die virussen delen met een cel?
- Welke elementen zijn van nature monatomisch?
- Wat is het seksuele systeem?
- Gekapte tropische regenwouden ondersteunen nog steeds de biodiversiteit, zelfs als de hitte aan staat
- Hoe zijn zowel een bewerkingen als een gevolgtrekking hoe ze verschillen?
- Wat zijn de activiteiten die betrokken zijn bij de wetenschappelijke methode?
- Wat zijn enkele menselijke lichaamswoorden?
- Wat maakt urine geel? Wetenschappers ontdekken het verantwoordelijke enzym
- Honden huilen meer als ze herenigd worden met hun baasjes
- Nieuw onderzoek combineert geluids- en lichtgolven in siliciumchips om een nieuw type signaalverwerking te creëren

- Fundamenteel effect van supergeleiderfysica waargenomen 30 jaar nadat het werd voorspeld

- Onderzoekers synthetiseren supergeleidend materiaal op kamertemperatuur

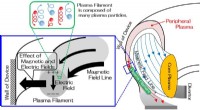
- Een miljard plasmadeeltjes berekenen in een supercomputer
- NIST lanceert een drastisch verbeterd systeem voor het meten van de intensiteit en het spectrum van licht
 Welk product produceren waterstofperoxide water luminol ammoniumcarbonaat natriumkopersulfaat pentahydraat?
Welk product produceren waterstofperoxide water luminol ammoniumcarbonaat natriumkopersulfaat pentahydraat?  Waarom een toekomstige Apple-FBI-zaak heel anders kan verlopen
Waarom een toekomstige Apple-FBI-zaak heel anders kan verlopen  Een manier om de structurele stabiliteit in gespannen halide perovskieten te vergroten
Een manier om de structurele stabiliteit in gespannen halide perovskieten te vergroten Het atoomnummer is dat van een atoom?
Het atoomnummer is dat van een atoom?  Wat zijn de namen van sterren op Orion?
Wat zijn de namen van sterren op Orion?  Ontwerpen van stedelijke energiesystemen op basis van het stadsklimaat
Ontwerpen van stedelijke energiesystemen op basis van het stadsklimaat Stijgende temperaturen beperken de capaciteit van de oceanen om koolstof op te slaan
Stijgende temperaturen beperken de capaciteit van de oceanen om koolstof op te slaan Wat is het meest massaal nuttige ding dat een interstellaire lifter kan hebben in boek Hitchhikers Guide to Galaxy?
Wat is het meest massaal nuttige ding dat een interstellaire lifter kan hebben in boek Hitchhikers Guide to Galaxy?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

