
Wetenschap
Gehoorzaamt een bal die in een willekeurige richting wordt gegooid de vergelijking van de projectielbeweging?
$$\overrightarrow r=\overrightarrow{v_0}t+\frac{1}{2}\overrightarrow{g}t^2$$
waarbij \(\overrightarrow r\) de positie van de bal is op tijdstip \(t\), \(\overrightarrow{v_0}\) de beginsnelheid van de bal is, \(\overrightarrow{g}\) de versnelling als gevolg van de zwaartekracht, en \(t\) is de tijd.
Deze vergelijking geldt voor elk object dat in twee dimensies beweegt onder invloed van de zwaartekracht, ongeacht de richting waarin het wordt geworpen. De enige beperking is dat het object in een vlak evenwijdig aan de grond moet bewegen.
Laten we het volgende voorbeeld bekijken om te zien hoe de vergelijking van de projectielbeweging van toepassing is op een bal die in een willekeurige richting wordt gegooid. Stel dat een bal met een beginsnelheid van 10 m/s onder een hoek van 30 graden boven de horizontaal wordt gegooid. De vergelijking van de projectielbeweging voor deze bal is:
$$\overrightarrow r=(10\cos30^\circ)\hat{i}+(10\sin30^\circ)t\hat{j}-\frac{1}{2}gt^2\hat{j }$$
waarbij \(\hat{i}\) en \(\hat{j}\) respectievelijk de eenheidsvectoren in horizontale en verticale richting zijn.
Deze vergelijking kan worden gebruikt om op elk moment \(t\) de positie van de bal te berekenen. Op tijdstip \(t =1\text{ s}\) is de positie van de bal bijvoorbeeld:
$$\overrightarrow r=(10\cos30^\circ)\hat{i}+(10\sin30^\circ)(1\text{ s})\hat{j}-\frac{1}{2} (9,8\text{ m/s}^2)(1\text{ s})^2\hat{j}$$
$$=(8,66\text{ m})\hat{i}+(5\text{ m})\hat{j}-(4,9\text{ m})\hat{j}$$
$$=(8,66\tekst{ m})\hat{i}+(0,1\text{ m})\hat{j}$$
De bal bevindt zich dus op 8,66 m van het startpunt in horizontale richting en op 0,1 m van het startpunt in verticale richting.
De bewegingsvergelijking van projectielen kan worden gebruikt om een verscheidenheid aan problemen op te lossen die te maken hebben met de beweging van objecten onder invloed van de zwaartekracht. Het kan bijvoorbeeld worden gebruikt om het bereik van een projectiel, de maximale hoogte van een projectiel en de vluchttijd van een projectiel te berekenen.
 Nieuw materiaal om wonden te behandelen kan beschermen tegen resistente bacteriën
Nieuw materiaal om wonden te behandelen kan beschermen tegen resistente bacteriën Wat is het aantal ongepaarde elektronen in een lithiumatoom?
Wat is het aantal ongepaarde elektronen in een lithiumatoom?  Volatiliteitsverrassingen ontstaan bij het verwijderen van overtollig waterstof
Volatiliteitsverrassingen ontstaan bij het verwijderen van overtollig waterstof Waarom wordt bij blanco-titratie meer volume HCl gebruikt dan bij volume-olietitratie?
Waarom wordt bij blanco-titratie meer volume HCl gebruikt dan bij volume-olietitratie?  Ongebruikelijke kobaltverbinding ontwikkeld voor dunnefilmproductie
Ongebruikelijke kobaltverbinding ontwikkeld voor dunnefilmproductie
 Wetenschappers vinden recept voor groenere verwijdering van tuinafval
Wetenschappers vinden recept voor groenere verwijdering van tuinafval Overeenkomsten en verschillen tussen kikkers en padden
Overeenkomsten en verschillen tussen kikkers en padden Fossiele bladeren vertonen een hoge atmosferische koolstof die de oude wereldwijde vergroening heeft gestimuleerd
Fossiele bladeren vertonen een hoge atmosferische koolstof die de oude wereldwijde vergroening heeft gestimuleerd Wat droogt de landruimte op?
Wat droogt de landruimte op?  Bio-kolen maken van plantaardig afval om klimaatverandering tegen te gaan
Bio-kolen maken van plantaardig afval om klimaatverandering tegen te gaan
Hoofdlijnen
- De langste mensen ter wereld delen deze merkwaardige eigenschappen
- Om erwtenplaten te produceren die alleen de recessieve phenitypw van een eigenschap vertonen, wat moeten de genotypen van de ouderplaten zijn?
- Wat de levendige pigmenten van vogelveren ons kunnen leren over hoe evolutie werkt
- Bewijs dat mensen de wereld opnieuw hebben vormgegeven? Kippen
- Rechtshandige gewoonte is misschien 2 miljoen jaar geleden begonnen
- Hoe lokale ecologische kennis bedreigde en zeldzame dieren kan redden
- Onderzoekers ontdekken hoe natuurlijke medicijnen ontstekingen bestrijden
- Waarom zijn strikte aërobe oxidase positief?
- Het grootste onderzoek naar de groei van de dinosauruspopulatie ooit laat zien hoe Maiasaura leefde en stierf
- De gecoördineerde dans tussen elektronen en kernen vastleggen in een door licht opgewekt molecuul
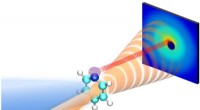
- Oplossen van nucleaire structuur in lichte kernen

- Masker dragen combineren, social distancing onderdrukt de verspreiding van het COVID-19-virus
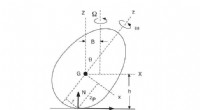
- Waarom staat een draaiend ei rechtop?
- Knippert helder wanneer hij stevig wordt samengedrukt:hoe eencellige organismen de oceanen verlichten
 Ricine alleen dodelijk in combinatie met suiker
Ricine alleen dodelijk in combinatie met suiker Wat is Pi-dag? Waarom wiskundigen en bakkers zich verenigen om feest te vieren
Wat is Pi-dag? Waarom wiskundigen en bakkers zich verenigen om feest te vieren Wat zijn de soorten dichte bindweefsels?
Wat zijn de soorten dichte bindweefsels?  Lichtgevende kwantumstippen zouden de synthese van nieuwe verbindingen kunnen vergemakkelijken
Lichtgevende kwantumstippen zouden de synthese van nieuwe verbindingen kunnen vergemakkelijken Methaan:emissies nemen toe en dat is geen goed nieuws
Methaan:emissies nemen toe en dat is geen goed nieuws Wat doet de temporale kwab?
Wat doet de temporale kwab?  Team werpt nieuw licht op fotosynthese
Team werpt nieuw licht op fotosynthese IAEA steunt vrijkomen verontreinigd Fukushima-water in zee
IAEA steunt vrijkomen verontreinigd Fukushima-water in zee
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

