
Wetenschap
Als een bewegende goederenwagen zachtjes in botsing komt met de goederenwagen in rust en de twee goederenwagens samen bewegen, zal hun gecombineerde momentum dan zijn?
Vóór de botsing is het totale momentum van het systeem:
$$P_i =m_1v_1 + m_2(0)$$
waar:
- \(P_i\) is het totale initiële momentum
- \(m_1\) is de massa van de bewegende gesloten goederenwagen
- \(v_1\) is de snelheid van de bewegende gesloten goederenwagen
- \(m_2\) is de massa van de gesloten goederenwagen in rust
Na de botsing bewegen de twee goederenwagens samen met een gemeenschappelijke snelheid \(v\). Het totale momentum van het systeem na de botsing is:
$$P_f =(m_1 + m_2)v$$
Omdat het totale momentum van het systeem behouden moet blijven, hebben we:
$$P_i =P_f$$
$$m_1v_1 + m_2(0) =(m_1 + m_2)v$$
Als we \(v\) oplossen, krijgen we:
$$v =\frac{m_1v_1}{m_1 + m_2}$$
Deze uitdrukking geeft ons de snelheid van de twee gesloten goederenwagens na de botsing. Het gecombineerde momentum van de twee gesloten goederenwagens na de botsing is:
$$P =(m_1 + m_2)v =\frac{m_1m_2v_1}{m_1 + m_2}$$
Daarom is het gecombineerde momentum van de twee gesloten goederenwagens na de botsing gelijk aan het momentum van de bewegende gesloten goederenwagen vóór de botsing, gedeeld door de som van de massa's van de twee gesloten goederenwagens.
 Zijde kan de gevoeligheid verbeteren, flexibiliteit van draagbare lichaamssensoren
Zijde kan de gevoeligheid verbeteren, flexibiliteit van draagbare lichaamssensoren Welk element ontstaat wanneer een waterstofbom ontploft?
Welk element ontstaat wanneer een waterstofbom ontploft?  Wat gebeurt er als zout wordt toegevoegd aan water?
Wat gebeurt er als zout wordt toegevoegd aan water?  Hoe kun je bepalen of een molecuul een hoger kookpunt heeft?
Hoe kun je bepalen of een molecuul een hoger kookpunt heeft?  Wat veroorzaakte een verandering in de chemische samenstelling van kustwateren tijdens orkaan Floyd?
Wat veroorzaakte een verandering in de chemische samenstelling van kustwateren tijdens orkaan Floyd?
 Elektriciteit opwekken met rijststro
Elektriciteit opwekken met rijststro Onder druk:hoe kamgelei zich heeft aangepast aan het leven op de bodem van de oceaan
Onder druk:hoe kamgelei zich heeft aangepast aan het leven op de bodem van de oceaan  Waarom hebben planten en dieren stikstof nodig?
Waarom hebben planten en dieren stikstof nodig?  Hawaï-gezinnen getroffen door lekkende vliegtuigbrandstof van de marine maken zich zorgen over kanker, bereiden een jaar later juridische stappen voor
Hawaï-gezinnen getroffen door lekkende vliegtuigbrandstof van de marine maken zich zorgen over kanker, bereiden een jaar later juridische stappen voor Filippijnse slangen soorten
Filippijnse slangen soorten
Hoofdlijnen
- Wat gebeurt er met cellen vanwege een natriumbalans?
- Nieuwe afbraakeiwitten tonen de route naar celoverleving
- Kikker en menselijke bloedcellen vergelijken en identificeren
- DNA van een Incajongen die 500 jaar geleden werd geofferd, laat zien hoe mensen zich naar Zuid-Amerika verspreidden
- Hoeveel water is er nodig om één liter melk te maken?
- Hoe is variatie gunstig voor een populatie van organismen?
- wat zijn de bestanddelen van voedsel?
- Vorm of functie? Evolutie volgt verschillende paden
- De kleinste krachten opsporen:hoe T-cellen indringers detecteren
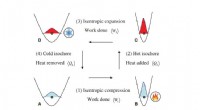
- Natuurkundigen onderzoeken fundamentele limieten van kwantummotoren
- Miniatuur magnetische zwemtoestellen om diagnostiek en medicijnafgifte te revolutioneren

- Quantumsystemen simuleren met neurale netwerken

- Gouden aanraking van onderzoekers verbetert kwantumtechnologie
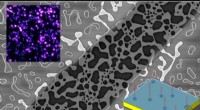
- Silicium nanoantennes regelen lichtverstrooiing voor optisch computergebruik

 Onderzoekers gebruiken antennes voor detectie van verplaatsing van angstrom
Onderzoekers gebruiken antennes voor detectie van verplaatsing van angstrom Hebben we biologisch afbreekbare kunststoffen nodig?
Hebben we biologisch afbreekbare kunststoffen nodig?  Wetenschappers onthullen hoe belangrijk kankerdoelwit de verspreiding van kanker kan stoppen
Wetenschappers onthullen hoe belangrijk kankerdoelwit de verspreiding van kanker kan stoppen Inwoners van Ohio vechten om Lake Erie wettelijke rechten te geven
Inwoners van Ohio vechten om Lake Erie wettelijke rechten te geven  Hector verzwakt maar blijft categorie 4 orkaan
Hector verzwakt maar blijft categorie 4 orkaan Mineralogie van de aardkorst drijft hotspots voor intraterrestrisch leven
Mineralogie van de aardkorst drijft hotspots voor intraterrestrisch leven Technische studenten maken een 3D-geprinte functionele robotarm
Technische studenten maken een 3D-geprinte functionele robotarm Verdunningsoplossingen berekenen
Verdunningsoplossingen berekenen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

