
Wetenschap
Wat Een bal heeft een massa van 0,25 kg en beweegt met een snelheid van 1,0 m/s naar rechts. Het bereikt 0,15, wat aanvankelijk rust is. Verplaatst zich na botsing met een snelheid van 0,75 m/s.?
Het initiële momentum van het systeem is:
$$P_i =m_1v_1 + m_2v_2$$
$$P_i =(0,25 kg)(1,0 m/s) + (0,15 kg)(0 m/s) =0,25 kg m/s$$
Na de botsing hebben de bal en de andere bal een snelheid van respectievelijk 0,75 m/s en v_2. Het totale momentum van het systeem na de botsing is:
$$P_f =m_1v_1' + m_2v_2'$$
$$P_f =(0,25 kg)(0,75 m/s) + (0,15 kg)v_2'$$
Door behoud van momentum hebben we:
$$P_i =P_f$$
$$0,25 kg m/s =(0,25 kg)(0,75 m/s) + (0,15 kg)v_2'$$
Als we v_2' oplossen, krijgen we:
$$v_2' =\frac{0,25 kg m/s - (0,25 kg)(0,75 m/s)}{0,15 kg} =0,5 m/s$$
Daarom beweegt de andere bal na de botsing naar rechts met een snelheid van 0,5 m/s.
 Radicale moleculen vangen voordat ze verdwijnen
Radicale moleculen vangen voordat ze verdwijnen Onderzoekers onthullen gastreactiegestuurde kooi aan Siamese tweelingkooi, mitose-achtige gastheertransformatie
Onderzoekers onthullen gastreactiegestuurde kooi aan Siamese tweelingkooi, mitose-achtige gastheertransformatie Wat is de uitgebalanceerde vergelijking voor zilver- en zinknitraat?
Wat is de uitgebalanceerde vergelijking voor zilver- en zinknitraat?  Koperkatalysator zorgt voor een zeer efficiënte omzetting van CO2 naar brandstoffen
Koperkatalysator zorgt voor een zeer efficiënte omzetting van CO2 naar brandstoffen Onderzoeksteam ontwerpt kleinschalige chemische neus
Onderzoeksteam ontwerpt kleinschalige chemische neus
 Watersporters en vissers moesten helpen bij het opnieuw in kaart brengen van door orkaan Irma . gewijzigde waterwegen
Watersporters en vissers moesten helpen bij het opnieuw in kaart brengen van door orkaan Irma . gewijzigde waterwegen Wetenschappers gaan nieuwe locaties in Puerto Rico verkennen, USVI-wateren
Wetenschappers gaan nieuwe locaties in Puerto Rico verkennen, USVI-wateren Twee voorbeelden van hoe de Nijl het oude Egypte vormde
Twee voorbeelden van hoe de Nijl het oude Egypte vormde  Work How Caterpillar schrankladers en multi-terrain
Work How Caterpillar schrankladers en multi-terrain  Reconstructie toont toegenomen trends in opwarming van de aarde sinds 1850
Reconstructie toont toegenomen trends in opwarming van de aarde sinds 1850
Hoofdlijnen
- Wat heeft Mendel waargenomen bij de F2-nakomelingen waaruit bleek dat allelen voor zaadvorm onafhankelijk van die kleur segregeren?
- Zijn de hersenen bedraad voor religie?
- Rode wouwkuikens geboren tijdens droogte hebben littekens voor het leven:de verborgen bedreiging van klimaatverandering voor natuurbehoud
- Kunnen we 11 miljard mensen voeden en tegelijkertijd de verspreiding van infectieziekten voorkomen?
- Bij de VN is overeenstemming bereikt over het biopiraterijverdrag
- Hoe vogelvoeders kleine soorten helpen infecties te bestrijden
- Welke kenmerken delen de meeste bacteriën?
- In het blauw:hoe baleinwalvissen zich de afgelopen 50 miljoen jaar hebben aangepast
- Nieuwe bananenziekte verspreidt zich en vormt een bedreiging voor de voedselzekerheid van Afrika
- Veel knoppen voor een bloesem:een synchronisatiebenadering van detectie met behulp van veel oscillatoren
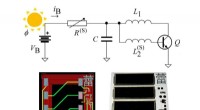
- Nieuwe holografische techniek maakt de weg vrij voor kwantumberekening

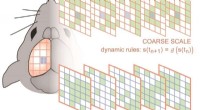
- Eigenaardige fysica aan het werk in de hersenen
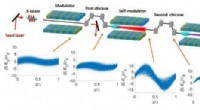
- Wetenschappers stellen een nieuw zelf-modulatieschema voor in gezaaide vrije-elektronenlasers
- Vlotte, veelzijdige on-chip lichtmanipulatie is nu mogelijk met supersymmetrie

 DIY: Stoomgenerator
DIY: Stoomgenerator  Cultuur assimileren – wat taal ons vertelt over immigratie en integratie
Cultuur assimileren – wat taal ons vertelt over immigratie en integratie  Het succes van 'Pokemon Go' roept de vraag op:hoe uitgebreid moet de werkelijkheid zijn?
Het succes van 'Pokemon Go' roept de vraag op:hoe uitgebreid moet de werkelijkheid zijn?  Een duidelijker beeld van hoe huurmoordenaars zich ontwikkelden
Een duidelijker beeld van hoe huurmoordenaars zich ontwikkelden  De eetlust van bacteriën kan de sleutel zijn tot het opruimen van antibioticabesmetting
De eetlust van bacteriën kan de sleutel zijn tot het opruimen van antibioticabesmetting China onderzoekt vermoedelijk lekken van klantgegevens bij Accor-partner
China onderzoekt vermoedelijk lekken van klantgegevens bij Accor-partner Onderzoekers tonen aan dat door laser geïnduceerd grafeen bacteriën doodt en biofouling tegengaat
Onderzoekers tonen aan dat door laser geïnduceerd grafeen bacteriën doodt en biofouling tegengaat  Iraniërs slagen erin om op internet te surfen ondanks de vloed van censuur
Iraniërs slagen erin om op internet te surfen ondanks de vloed van censuur
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

