
Wetenschap
Je draait een elektrisch dipooluiteinde voor in een uniform veld. Hoe hangt het werk dat je doet af van de initiële oriëntatie ten opzichte van het veld?
Terwijl je de dipool over een oneindig kleine hoek \(d\theta\) draait, verricht je een hoeveelheid werk
$$dW=(\overrightarrow{p}\cdot\overrightarrow{E})sin\theta d\theta=pEsin\theta d\theta$$
In een eindige rotatie van hoek \(\theta_1\) naar hoek \(\theta_2\), is de verrichte arbeid:
$$W=\int_{\theta_1}^{\theta_2}dW=pE\int_{\theta_1}^{\theta_2}sin\theta d\theta=pE(cos\theta_1+cos\theta_2)$$
In de bovenstaande vergelijking is \(\theta_1\) de beginhoek en \(\theta_2\) de eindhoek van de dipool ten opzichte van de veldrichting.
Om \(W\) alleen in termen van initiële oriëntatie te krijgen, vervangen we \(\theta_2=\pi-\theta_1\) in de bovenstaande vergelijking. Daarom
$$W=-2pEcos\theta_1$$
$$W\propto cos\theta_1$$
Deze vergelijking houdt in dat de arbeid maximaal is als de dipool aanvankelijk antiparallel is aan het veld en nul als deze aanvankelijk evenwijdig is.
 Wat is beter water of azijn in het tornadoflesexperiment?
Wat is beter water of azijn in het tornadoflesexperiment?  Bacteriën produceren goud door giftige metalen te verteren
Bacteriën produceren goud door giftige metalen te verteren Nieuwe ontdekking opent nieuwe weg voor productie met hoge titer van drop-in biobrandstoffen
Nieuwe ontdekking opent nieuwe weg voor productie met hoge titer van drop-in biobrandstoffen Beschrijft een chemische formule een reactie?
Beschrijft een chemische formule een reactie?  Nieuw waterfiltratieproces gebruikt 1, 000 keer minder energie
Nieuw waterfiltratieproces gebruikt 1, 000 keer minder energie
 Nieuw onderzoek onthult dat anaërobe vergisting de Britse netto-nul-emissies zou kunnen ondermijnen
Nieuw onderzoek onthult dat anaërobe vergisting de Britse netto-nul-emissies zou kunnen ondermijnen Atmosferische waarnemingen in China laten een stijging zien in de uitstoot van een krachtig broeikasgas
Atmosferische waarnemingen in China laten een stijging zien in de uitstoot van een krachtig broeikasgas  Leverde de hitte van de inslagen op asteroïden de ingrediënten voor het leven op aarde?
Leverde de hitte van de inslagen op asteroïden de ingrediënten voor het leven op aarde? Kunnen we miljarden voeden zonder de planeet te verwoesten?
Kunnen we miljarden voeden zonder de planeet te verwoesten? Australië maakt zich op voor het ergste nu het bosbrandseizoen vroeg begint
Australië maakt zich op voor het ergste nu het bosbrandseizoen vroeg begint
Hoofdlijnen
- Wat is de subclassificatie van fosfolipiden?
- Kan graszaad net zo goed groeien op een lavasteen als op aarde?
- Kleine vogels beschikken over een scala aan vliegstijlen dankzij hun evolutionaire voorsprong
- Epigenetische erfenis:een 'zilveren kogel' tegen klimaatverandering?
- Wat zijn drie dingen die bepalen of een molecuul in een celmembraan kan diffunderen?
- Fruitvlieg helpt bij het ontsluiten van aanwijzingen over hoe organen, weefsel en kanker groeien
- Wat is een vetzuur? | Hoe dingen werken
- Wat is mRNA? u moet op de hoogte zijn van het belangrijkste ingrediënt in sommige COVID-19-vaccins
- Nieuwe techniek maakt succesvolle kweek van stamcellen op het oppervlak van ionische vloeistoffen mogelijk
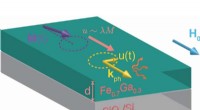
- Onderzoekers ontdekken de belangrijkste oorzaak van energieverlies in spintronische materialen
- Nieuw periodiek systeem van druppels kan helpen bij het oplossen van misdaden

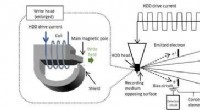
- Nieuwe analytische technologie voor de schrijfkop van de harde schijf kan de capaciteit van de harde schijf vergroten
- Video:HIE-ISOLDEs fase 2 bereikt voltooiing

- Ingenieurs brengen laserpulsen naar nieuwe dimensies

 Vraag ons ietsWelke van de volgende bevat een niet-polaire covalente binding?
Vraag ons ietsWelke van de volgende bevat een niet-polaire covalente binding?  Facebook negeert Brazilië-pagina's, profielen die nepnieuws verspreiden
Facebook negeert Brazilië-pagina's, profielen die nepnieuws verspreiden Hoe virussen veranderen De manier waarop we naar evolutie kijken
Hoe virussen veranderen De manier waarop we naar evolutie kijken  Structureel model van fysiologische tau-microtubuli-interacties werpt licht op neurologische ziekten
Structureel model van fysiologische tau-microtubuli-interacties werpt licht op neurologische ziekten Heeft de natuur een hand gehad bij de vorming van de Grote Sfinx?
Heeft de natuur een hand gehad bij de vorming van de Grote Sfinx?  Video:Complexe chemie in de koude diepten van de ruimte
Video:Complexe chemie in de koude diepten van de ruimte  Mangaan single-atom katalysator verhoogt de prestaties van elektrochemische kooldioxide-reductie
Mangaan single-atom katalysator verhoogt de prestaties van elektrochemische kooldioxide-reductie Wetenschappers weten eindelijk hoe grote aardbevingen beginnen:met veel kleinere
Wetenschappers weten eindelijk hoe grote aardbevingen beginnen:met veel kleinere
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

