
Wetenschap
Gebruik van thermodynamische geometrie om microscopische eindige-tijd-warmtemotoren te optimaliseren
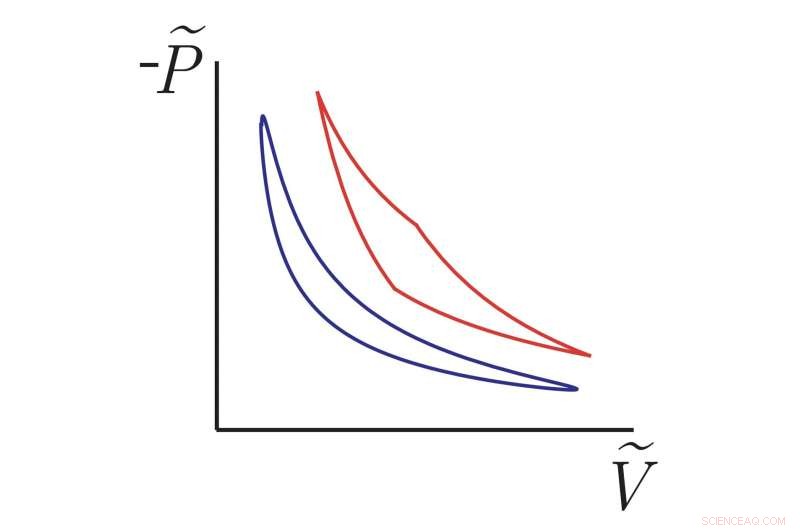
Nieuw ontdekte thermodynamische cycli (gladde blauwe curve) benaderen een nieuwe geometrische grens aan efficiëntie en presteren beter dan andere niet-evenwichtsmotoren zoals de Carnot-cyclus (rode curve) die in eindige tijd werkt. De verticale en horizontale assen vertegenwoordigen analogen van (negatieve) druk en volume voor een microscopische motor die bestaat uit een deeltje dat aan een veer is bevestigd en wordt geteisterd door thermische fluctuaties vanuit zijn omgeving. Dit zijn theoretische krommen die zijn gebaseerd op onze wiskundige resultaten, maar experimentatoren hebben onlangs methoden ontwikkeld om de efficiëntie van dit soort systemen te meten, zodat onze resultaten kunnen worden getest. Krediet:Frim &DeWeese.
Stochastische thermodynamica is een opkomend gebied van de natuurkunde dat is gericht op een beter begrip en interpretatie van thermodynamische concepten weg van evenwicht. In de afgelopen jaren hebben bevindingen op deze gebieden een revolutie teweeggebracht in het algemene begrip van verschillende thermodynamische processen die in een eindige tijd werken.
Adam Frim en Mike DeWeese, twee onderzoekers aan de University of California, Berkeley (UC Berkeley), hebben onlangs een theoretische studie uitgevoerd waarin ze de volledige ruimte van thermodynamische cycli met een continu veranderende badtemperatuur hebben onderzocht. Hun resultaten, gepresenteerd in een paper gepubliceerd in Physical Review Letters , werden verkregen met behulp van geometrische methoden. Thermodynamische geometrie is een benadering om de respons van thermodynamische systemen te begrijpen door middel van het bestuderen van de geometrische regelruimte.
"Bijvoorbeeld, voor een gas in een zuiger, zou een coördinaat in deze controleruimte kunnen overeenkomen met het experimenteel gecontroleerde volume van het gas en een andere met de temperatuur", vertelde DeWeese aan Phys.org. "Als een experimentator aan die knoppen zou draaien, tekent dat een traject in deze thermodynamische ruimte uit. Wat de thermodynamische geometrie doet, is aan elke curve een 'thermodynamische lengte' toewijzen die overeenkomt met de minimaal mogelijke gedissipeerde energie van een bepaald pad. "
Thermodynamische geometrie stelt onderzoekers in staat om interessante onderzoeksvragen te onderzoeken, zoals de optimale manier om een bepaald nanoscopisch systeem te manipuleren, een beetje informatie te wissen of een klassieke of kwantumwarmtemotor te bouwen.
"Ons hoofddoel in dit artikel was om de meest efficiënte manier te vinden om een microscopisch kleine motor te laten draaien, zodat deze het meest bruikbare werk levert voor de hoeveelheid brandstof die hij verbruikt," vertelde DeWeese aan Phys.org. "Terwijl de meeste eerdere thermodynamische geometriestudies gericht waren op het optimaliseren van de besturing van een systeem met een bepaalde begin- en eindinstelling, waren we geïnteresseerd in het construeren van optimale gesloten krommen die zouden kunnen functioneren als zeer efficiënte warmtemotoren."
De belangrijkste "regels" om te begrijpen hoe grote motoren, zoals die in auto's, wanneer ze langzaam worden gebruikt, efficiënt kunnen worden gebruikt, werden meer dan een eeuw geleden voor het eerst uiteengezet, toen de wetten van de thermodynamica voor het eerst werden geformuleerd. In hun paper breidden Frim en DeWeese deze theorieën uit, zodat ze ook konden worden toegepast op microscopisch kleine motoren die in een eindige tijd werken. In tegenstelling tot langzaam draaiende grote motoren zijn deze motoren niet in thermisch evenwicht met de buitenwereld en worden ze sterk beïnvloed door thermische schommelingen in de omgeving.
"In elke niet-gegradueerde cursus thermodynamica leren we dat als je de druk uitzet tegen het volume van een gas in een cilinder en elke gesloten cyclus beschouwt die terugkeert naar hetzelfde punt in de grafiek, het gebied binnen de curve je de hoeveelheid bruikbare werk dat je krijgt van één cyclus van deze warmtemotor," zei DeWeese. "Hierbij wordt ervan uitgegaan dat je heel langzaam rond de cyclus beweegt, zodat het gas in de cilinder altijd dicht bij evenwicht blijft met de buitenwereld. Er is een analogie met dit P-V-diagram voor microscopische motoren, zoals een klein deeltje dat aan een veer is bevestigd wordt geteisterd door thermische fluctuaties vanuit de omgeving."
Toen ze cycli uitzetten naar analogie van een PV-diagram voor een microscopische motor, ontdekten Frim en DeWeese dat een bepaalde functie van het gebied binnen de gesloten curve nog steeds kon worden beschouwd als de hoeveelheid nuttig werk die door één cyclus van de motor wordt geleverd . Bovendien bleek de lengte van de gesloten curve gerelateerd te zijn aan de hoeveelheid "nuttig werk" dat verloren is gegaan door dissipatie (d.w.z. het opwarmen van de omgeving zonder naar de werking van de motor te gaan).
"Ons resultaat is conceptueel relatief eenvoudig", legt DeWeese uit. "In thermodynamische geometrie gaat lengte ongeveer als dissipatie. Dus we dachten toen:als je een cyclus (een gesloten lus) neemt met een omtrek die een vaste lengte heeft, wat stelt dan het gebied binnen deze lus voor? Het blijkt dat het gaat ongeveer als de werkoutput van de cyclus, dus eigenlijk zouden optimale cycli een lage dissipatie en een hoge output moeten hebben, d.w.z. een kleine lengte en een groot gebied."
Gebruikmakend van klassieke geometrische resultaten, konden de onderzoekers optimale protocollen identificeren die een grens stellen aan de efficiëntie van alle gesloten cycli. Hun bevindingen kunnen een belangrijke bijdrage leveren aan het ontwerp en de ontwikkeling van efficiënte microscopische warmtemotoren. De grens aan de efficiëntie van onomkeerbare thermodynamische cycli die door dit team van onderzoekers is vastgesteld, is algemeen, dus de implicaties ervan kunnen veel verder reiken dan de specifieke microscopische motoren die in hun paper worden beschouwd.
"Een van onze langetermijndoelen is om de theorie te ontwikkelen die ingenieurs nodig hebben om zeer kleine en efficiënte motoren te ontwerpen en te bouwen", zei DeWeese. "Dit kan een belangrijk gebied van nanotechnologie blijken te zijn. We zijn ook sterk gemotiveerd om de structuur en functie te begrijpen van de moleculaire motoren en andere soorten moleculaire 'machines' die we in de cellen van alle wezens en planten zien."
In hun werk veronderstellen De Weese en Frim dat natuurlijke evolutie mogelijk heeft gekozen voor efficiënte moleculaire machines. Als dit het geval zou zijn, zouden de regels die ze ontdekten een eerste stap kunnen zijn om de structuur en functie te kunnen voorspellen van moleculaire machines die alomtegenwoordig zijn in de biologie.
"Isoperimetrische ongelijkheden (dat wil zeggen, het samenspel van lengtes en gebieden van gesloten krommen) in geometrische benaderingen van de natuurkunde kunnen in de toekomst talloze implicaties hebben", voegde DeWeese eraan toe. "Onze wiskundige grens is realistischer dan eerdere resultaten die aannamen dat de motor te allen tijde zeer dicht bij thermisch evenwicht was met de omgeving (of het warmtebad), maar we nemen nog steeds aan dat het systeem langzaam wordt aangedreven (d.w.z. de regelparameters worden langzaam veranderd). We zijn nu geïnteresseerd in het uitbreiden van onze resultaten buiten dit regime om systemen te omvatten die verder van evenwicht zijn." + Verder verkennen
Geminiaturiseerde 'warmtemotoren' kunnen de nanoschaalmachines van de toekomst aandrijven
© 2022 Science X Network
 Een uitgebreide metabole kaart voor de productie van biogebaseerde chemicaliën
Een uitgebreide metabole kaart voor de productie van biogebaseerde chemicaliën Maak een lijst van enkele factoren die de diffusiesnelheid zouden verhogen
Maak een lijst van enkele factoren die de diffusiesnelheid zouden verhogen Smelten van banden
Smelten van banden Wetenschappers ontwikkelen duurzame manier om chitine uit garnalenschelpen te extraheren door het te vergisten met fruitafval
Wetenschappers ontwikkelen duurzame manier om chitine uit garnalenschelpen te extraheren door het te vergisten met fruitafval Baanbrekende ontdekkingen kunnen superieure legeringen creëren met veel toepassingen
Baanbrekende ontdekkingen kunnen superieure legeringen creëren met veel toepassingen
 Model suggereert dat het vastleggen van CO2 in diepzeesedimenten een haalbare optie kan zijn
Model suggereert dat het vastleggen van CO2 in diepzeesedimenten een haalbare optie kan zijn Europa maakt zich op voor recordbrekende hittegolf
Europa maakt zich op voor recordbrekende hittegolf Hoe we de effectiviteit van wereldwijde milieubescherming kunnen vergroten
Hoe we de effectiviteit van wereldwijde milieubescherming kunnen vergroten Enorme ijsberg breekt eindelijk af van Antarctica Larsen C Ice Shelf
Enorme ijsberg breekt eindelijk af van Antarctica Larsen C Ice Shelf  Milieuproblemen met hydrofracking verschillen niet zo veel van conventioneel boren
Milieuproblemen met hydrofracking verschillen niet zo veel van conventioneel boren
Hoofdlijnen
- Ecologen gebruiken de nieuwste tandheelkundige scantechnologie om jong koraal te bestuderen
- Chemische cocktail in de huid roept ziekteverspreidende muggen op
- Chemische reacties vereist voor het onderhoud van Homeostasis
- Vertaling (biologie): definitie, stappen, diagram
- Hartmonitors op wilde narwallen onthullen alarmerende reacties op stress
- Nestgebieden van schildpadden volgen
- Genomische analyse onthult de ware oorsprong van hondachtigen in Zuid-Amerika
- Heeft Kelp veel verschillende cellen?
- De ecologische kosten van oorlog:conflict een consequente moordenaar van Afrikaanse megafauna
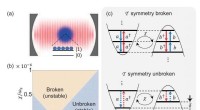
- Natuurkundigen onthulden spontane T-symmetrie breuken en uitzonderlijke punten in holte QED
- Onderzoekers gebruiken ruisgegevens om de betrouwbaarheid van kwantumcomputers te vergroten
- Samenwerking maakt kristalheldere studie van stralingsreactie mogelijk

- Nieuwe ontdekking beëindigt al lang bestaand debat over fotovoltaïsche materialen

- Een ultra-vrijheidsgraad gestructureerde vectorstraal

 Windparken efficiënter maken
Windparken efficiënter maken Uber gekoppeld aan een vermindering van ernstig verkeersgewonden in het VK
Uber gekoppeld aan een vermindering van ernstig verkeersgewonden in het VK geloof leiders, Pygmeeën bundelen krachten in strijd om Congobos
geloof leiders, Pygmeeën bundelen krachten in strijd om Congobos Mensen gebruiken kunstmatige intelligentie om hun scheiding te regelen. Zou jij?
Mensen gebruiken kunstmatige intelligentie om hun scheiding te regelen. Zou jij? Hubble ziet een prachtig spiraalstelsel
Hubble ziet een prachtig spiraalstelsel Biomedische ingenieurs ontwikkelen draagbare ademhalingsmonitor met kinderspeelgoed
Biomedische ingenieurs ontwikkelen draagbare ademhalingsmonitor met kinderspeelgoed Record-setting orkaan Dorian blijft het noorden van Bahama's beuken
Record-setting orkaan Dorian blijft het noorden van Bahama's beuken Exobiologie in een doos
Exobiologie in een doos
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

