
Wetenschap
Onderzoekers onderzoeken een nieuwe verbinding tussen topologie en kwantumverstrengeling
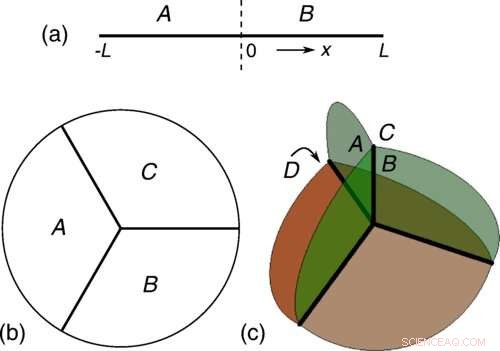
Het D-dimensionale Fermi-gas voor (a) D=1, (b) D=2 en (c) D=3 is verdeeld in D+1-gebieden die op één punt samenkomen, waarbij alle k-gebieden een vlakke grens delen van afmeting D + 1 - k. Hier bestuderen we een verstrengelingsmaat, bekend als de wederzijdse informatie, die de intrinsieke correlaties tussen alle D + 1-regio's vastlegt. De onderlinge informatie is topologisch in die zin dat deze een leidende logaritmische divergentie vertoont die evenredig is met de Euler-karakteristiek χF van de Fermi-zee. Credit:Pok Man Tam et al, Physical Review X (2022). DOI:10.1103/PhysRevX.12.031022
Topologie en verstrengeling zijn twee krachtige principes voor het karakteriseren van de structuur van complexe kwantumtoestanden. In een nieuw artikel in het tijdschrift Physical Review X , leggen onderzoekers van de Universiteit van Pennsylvania een verband tussen de twee.
"Ons werk verbindt twee grote ideeën met elkaar", zegt Charles Kane, de Christopher H. Browne Distinguished Professor of Physics in Penn's School of Arts &Sciences. "Het is een conceptueel verband tussen topologie, een manier om de universele kenmerken van kwantumtoestanden te karakteriseren, en verstrengeling, wat een manier is waarop kwantumtoestanden niet-lokale correlaties kunnen vertonen, waarbij iets dat op één punt in de ruimte gebeurt, is gecorreleerd met iets dat in een ander deel van de ruimte gebeurt. Wat we hebben gevonden is een situatie waarin die concepten nauw met elkaar verweven zijn."
Het zaad voor het verkennen van deze verbinding kwam tijdens de lange uren die Kane tijdens de pandemie in zijn thuiskantoor doorbracht, nadenkend over nieuwe ideeën. Eén gedachtegang bracht hem ertoe zich het klassieke leerboekbeeld voor te stellen van het Fermi-oppervlak van koper, dat de potentiële elektronenenergieën van het metaal vertegenwoordigt. Het is een foto die elke natuurkundestudent ziet, en een foto waarmee Kane zeer bekend was.
"Natuurlijk leerde ik in de jaren tachtig over die foto, maar ik had er nooit aan gedacht dat het een topologisch oppervlak zou beschrijven", zegt Kane.
Een klassieke manier van denken over topologische oppervlakken, zegt Kane, is om het verschil tussen een donut en een bol te overwegen. Wat is het verschil? Een enkel gat. Topologie beschouwt deze generaliseerbare eigenschappen van een oppervlak, die niet worden veranderd door vervorming. Volgens dit principe zouden een koffiekopje en een donut dezelfde topologische eigenschap hebben.
Gezien het Fermi-oppervlak van koper als een topologisch object, is het bijbehorende aantal gaten dat het bezit vier, een cijfer dat ook bekend staat als een geslacht. Toen Kane op deze manier over het Fermi-oppervlak begon te denken, vroeg hij zich af of er een relatie zou kunnen bestaan tussen het geslacht en kwantumverstrengeling.
Om die mogelijke connectie verder te onderzoeken, betrok Kane zijn afgestudeerde student Pok Man Tam en Martin Claassen, een assistent-professor natuurkunde aan Penn die zich in zijn werk heeft gericht op kwantumverstrengeling. Samen hebben ze een wiskundige relatie afgeleid tussen het geslacht van het Fermi-oppervlak en een mate van kwantumverstrengeling die de wederzijdse informatie wordt genoemd. De wederzijdse informatie kenmerkt de correlaties die kunnen optreden in ongelijksoortige gebieden van de ruimte die elkaar op één punt ontmoeten. Een getal dat bekend staat als het Euler-kenmerk, dat nauw verwant is aan het geslacht, zorgde voor het precieze verband tussen de twee.
De onderzoekers stelden vast dat de relatie tussen topologie en verstrengeling in een eenvoudig metalen systeem wordt vastgehouden, waarbij elektronen onafhankelijk van elkaar bewegen, en breidden vervolgens hun analyse uit om aan te tonen dat de verbinding ook aanwezig was, zelfs wanneer elektronen met grotere complexiteit interageren.
En hoewel het theoretische werk aan metalen werd gedaan, gelooft Kane dat het zich ook zal uitstrekken tot andere materialen, zoals die met zeer sterke interacties tussen elektronen.
"Dit stelt ons misschien in staat om nieuwe manieren van denken te bedenken over fasen van materie die we niet zo goed begrijpen en die we niet zo veel hulpmiddelen hebben om te verkennen", zegt Kane. "Mensen proberen erachter te komen hoe ze kwantummechanica kunnen gebruiken om te profiteren van kwantuminformatie. Om dat te doen, moet je begrijpen hoe kwantummechanica zich manifesteert als je veel vrijheidsgraden hebt. Dat is een heel moeilijk probleem, en dit werk duwt ons in die richting."
In follow-up work, Kane and colleagues hope to design experiments that continue to explore the newfound link, perhaps devising a new technique to measure the topological genus and a way to probe the structure of quantum entanglement. + Verder verkennen
Physicists find signatures of highly entangled quantum matter
 NASA vindt zware regenval in tyfoon Bualoi boven Marianas
NASA vindt zware regenval in tyfoon Bualoi boven Marianas CO2-monitors nieuw wapen in klimaatstrijd Parijs
CO2-monitors nieuw wapen in klimaatstrijd Parijs Californië bosbranden enkele van de grootste in de geschiedenis van de staat
Californië bosbranden enkele van de grootste in de geschiedenis van de staat Klimaatverandering test de veerkracht van inheemse planten tegen vuur, van essenbossen tot gymea-lelies
Klimaatverandering test de veerkracht van inheemse planten tegen vuur, van essenbossen tot gymea-lelies Mysterieziekte verspreidt zich, bedreigt koraalriffen in Lower Florida Keys
Mysterieziekte verspreidt zich, bedreigt koraalriffen in Lower Florida Keys
Hoofdlijnen
- Wat is de chemische vergelijking voor aërobe ademhaling?
- Zijn linkshandigen snellere denkers dan rechtshandigen?
- RNA (ribonucleïnezuur): definitie, functie, structuur
- Ozonvervuiling bedreigt de gezondheid van planten en maakt het voor bestuivers moeilijker om bloemen te vinden
- Feiten over de Spleen
- Zijn mannen of vrouwen betere navigators?
- Bioprocessing-ingenieurs winnen glucosinolaat uit oliezaadmeel
- Aminozuursupplement is een sleutel tot reproductieve gezondheid bij melkkoeien
- Eenvoudig epitheelweefsel: definitie, structuur en voorbeelden
- Ionenstralen betekenen een kwantumsprong voor qubits met kleurcentrum

- SDR-35 PVC pijp specificaties

- Eerste meting van interacties met één proton met de MicroBooNE-detector

- Optische spectroscopie verbetert de voorspellende beoordeling van de nierfunctie
- Hoe de 18e-eeuwse stoommachine natuurkundigen hielp een kwantumdoorbraak te maken

 Nieuwe ultrahete Jupiter-exoplaneet ontdekt
Nieuwe ultrahete Jupiter-exoplaneet ontdekt Heeft de zuurstof van de aarde de maan miljarden jaren verroest?
Heeft de zuurstof van de aarde de maan miljarden jaren verroest? Natuurkundige bespreekt eRosita-missie
Natuurkundige bespreekt eRosita-missie Armere gemeenschappen hebben empowerment nodig om weerbaarder te worden tegen natuurrampen
Armere gemeenschappen hebben empowerment nodig om weerbaarder te worden tegen natuurrampen Stabiele perovskiet-LED's een stap dichterbij
Stabiele perovskiet-LED's een stap dichterbij Waar is 's werelds grootste populatie adelaarsvaren?
Waar is 's werelds grootste populatie adelaarsvaren?  Handbediend NMR-instrument levert snelle analyse van menselijke tumoren op
Handbediend NMR-instrument levert snelle analyse van menselijke tumoren op Studie is gericht op het stimuleren van de antitumorale activiteit van een verbinding die is geëxtraheerd uit een Amazone-plant
Studie is gericht op het stimuleren van de antitumorale activiteit van een verbinding die is geëxtraheerd uit een Amazone-plant
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

