Wetenschap
Topologie in de biologie verkennen
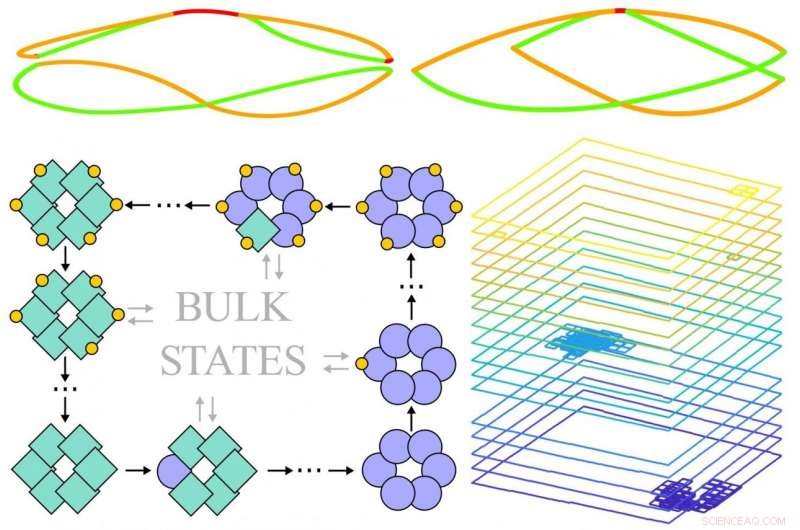
Boven:Zoals een S verandert in een O, het spectrum van een biochemisch systeem kan een topologische overgang ondergaan. Linksonder:In de topologisch beschermde staat, het biochemische systeem ondergaat randcycli. In dit voorbeeld, een eiwitcomplex dat bestaat uit zes subeenheden die van vorm kunnen veranderen (groen vierkant of paarse cirkel) of een ander molecuul kunnen binden (gele cirkels) vertoont randcycli waarbij alle subeenheden van vorm veranderen, een molecuul binden, allemaal weer van vorm veranderen, en laat uiteindelijk het molecuul los. Rechtsonder:het volgen van het traject van het systeem in de loop van de tijd laat zien dat randcycli zeer persistent zijn. Credit:Max Planck Instituut voor Dynamiek en Zelforganisatie
Wanneer kunnen we zeggen dat een bepaalde eigenschap van een systeem robuust is? Intuïtief, robuustheid houdt in dat zelfs onder invloed van externe verstoringen op het systeem, hoe sterk of willekeurig ook, genoemde eigenschap blijft ongewijzigd. In wiskunde, eigenschappen van een object die robuust zijn tegen vervormingen worden topologisch genoemd. Bijvoorbeeld, de letters s, S, en L kunnen in elkaar worden omgezet door hun vorm uit te rekken of te buigen. Hetzelfde geldt voor letters o, O, en D. Echter, het is onmogelijk om een S in een O te veranderen zonder een discontinue operatie, zoals het uit elkaar knippen van de O of het aan elkaar plakken van de twee uiteinden van de S. Daarom, we zeggen dat de letters s, S en L hebben dezelfde topologie, net als de letters o, O en D, terwijl de twee groepen letters verschillende topologieën hebben. Maar hoe verhoudt topologie zich tot biologie?
"In de afgelopen decennia is natuurkundigen hebben ontdekt dat bepaalde eigenschappen van kwantumsystemen alleen afhankelijk zijn van de topologie van een onderliggend kenmerk van het systeem, zoals de fase van zijn golffunctie of zijn energiespectrum", legt Evelyn Tang uit, co-eerste auteur van de studie. "We wilden weten of dit model ook kan worden toegepast op biochemische systemen om processen die uit balans zijn beter te beschrijven en te begrijpen." Omdat topologie ongevoelig is voor continue verstoringen, zoals het uitrekken of buigen van letters in het bovenstaande voorbeeld, zijn eigenschappen die aan topologie zijn gekoppeld, buitengewoon robuust. Ze blijven ongewijzigd tenzij er een kwalitatieve verandering in het systeem plaatsvindt, zoals het uit elkaar knippen of aan elkaar plakken van de bovenstaande letters. De wetenschappers Evelyn Tang, Jaime Agudo-Canalejo en Ramin Golestanian hebben nu aangetoond dat hetzelfde concept van topologische bescherming kan worden gevonden in biochemische systemen, die de robuustheid van de overeenkomstige biochemische processen garandeert.
Vloeiend langs de randen
Een van de bekendste observaties met betrekking tot topologie in kwantumsystemen is het kwantum Hall-effect:dit fenomeen treedt op wanneer een tweedimensionaal geleidend materiaal wordt onderworpen aan een loodrecht magnetisch veld. In zo'n omgeving, de elektronen in het materiaal beginnen te bewegen in kleine cirkels die bekend staan als cyclotron E-banen, die over het algemeen niet leiden tot enige netto stroom in het grootste deel van het materiaal. Echter, aan de randen van het materiaal, de elektronen zullen terugkaatsen voordat ze een baan voltooien, en effectief in de tegenovergestelde richting bewegen, wat resulteert in een netto stroom van elektronen langs deze randen. belangrijk, deze randstroom zal onafhankelijk van de vorm van de randen plaatsvinden, en zal blijven bestaan, zelfs als de randen sterk vervormd zijn, het benadrukken van de topologische en dus robuuste aard van het effect.
De onderzoekers merkten een parallel op tussen dergelijke cyclotronbanen in het kwantum Hall-effect en een waarneming in biochemische systemen die 'futile cycles' worden genoemd:gerichte reactiecycli die energie verbruiken maar nutteloos zijn, althans op het eerste gezicht. Bijvoorbeeld, een chemische stof A kan worden omgezet in B, die wordt omgezet in C, die vervolgens weer wordt omgezet in A. Dit riep de vraag op:is het mogelijk dat, zoals voor cyclotronbanen in het kwantum Hall-effect, zinloze cycli randstromen kunnen veroorzaken die resulteren in een netto stroming in een tweedimensionaal biochemisch reactienetwerk?
Zo modelleerden de auteurs biochemische processen die plaatsvinden in een tweedimensionale ruimte. Een eenvoudig voorbeeld is de assemblagedynamiek van een biopolymeer dat is samengesteld uit twee verschillende subeenheden X en Y:een zinloze cyclus met de klok mee zou dan overeenkomen met het toevoegen van een Y-subeenheid, het toevoegen van een X-subeenheid, het verwijderen van een Y-subeenheid, en het verwijderen van een X-subeenheid, die het systeem terug zou brengen naar de oorspronkelijke staat. Nutsvoorzieningen, zo'n tweedimensionale ruimte zal ook "randen" hebben, die beperkingen in de beschikbaarheid van subeenheden vertegenwoordigen. Als verwacht, de onderzoekers ontdekten dat stromingen tegen de klok in langs deze randen inderdaad spontaan zouden ontstaan. Jaime Agudo-Canalejo, co-eerste auteur van de studie, legt uit:"In deze biochemische context, randstromen komen overeen met grootschalige cyclische oscillaties in het systeem. In het voorbeeld van een biopolymeer, ze zouden resulteren in een cyclus waarin eerst alle X-subeenheden in het systeem aan het polymeer worden toegevoegd, gevolgd door alle Y-subeenheden, dan worden eerst alle X en tenslotte alle Y-subeenheden weer verwijderd, dus de cyclus is voltooid."
De kracht van topologie
Net als in het kwantum Hall-systeem, deze biochemische randstromen lijken bestand tegen veranderingen in de vorm van de systeemgrenzen of wanorde in het grootste deel van het systeem. De onderzoekers wilden dus onderzoeken of topologie inderdaad de kern vormt van deze robuustheid. Echter, de tools die in kwantumsystemen worden gebruikt, zijn niet direct toepasbaar op biochemische systemen, die ten grondslag liggen aan klassiek, stochastische wetten. Hiertoe, de onderzoekers bedachten een mapping tussen hun biochemische systeem en een exotische klasse van systemen die bekend staat als niet-Hermitische kwantumsystemen. Evelien Tang, die een achtergrond heeft in topologische kwantummaterie, herinnert eraan dat "wanneer deze mapping eenmaal was vastgesteld, de hele gereedschapskist van topologische kwantumsystemen kwam voor ons beschikbaar. Dat zouden we dan kunnen laten zien, inderdaad, randstromen zijn robuust dankzij topologische bescherming. Bovendien, we ontdekten dat de opkomst van randstromen onlosmakelijk verbonden is met de onevenwichtige aard van de futiele cycli, die worden aangedreven door energieverbruik."
Een nieuw rijk aan mogelijkheden
De robuustheid die voortvloeit uit topologische bescherming, gekoppeld aan de veelzijdigheid die inherent aanwezig is in biochemische netwerken, resulteert in een veelheid aan verschijnselen die in deze systemen kunnen worden waargenomen. Voorbeelden zijn een opkomende moleculaire klok die bepaalde kenmerken van circadiane systemen kan reproduceren, dynamische groei en krimp van microtubuli (eiwitten van het celskelet) en spontane synchronisatie tussen twee of meer systemen die zijn gekoppeld via een gedeelde pool van bronnen. Ramin Golestanian, co-auteur van de studie en directeur van de afdeling Living Matter Physics bij MPI-DS, is optimistisch voor de toekomst. "Onze studie stelt voor, Voor de eerste keer, minimale biochemische systemen waarin topologisch beschermde randstromen kunnen ontstaan. Gezien de rijkdom aan biochemische netwerken die in de biologie bestaan, we geloven dat het slechts een kwestie van tijd is voordat er voorbeelden worden gevonden waarin topologische bescherming de operaties in dergelijke systemen gevoelig controleert."
 Dingen die een ecosysteem maken
Dingen die een ecosysteem maken Milieuvernuft:deze creatieve zakelijke ideeën zijn bedoeld om zowel duurzaam als succesvol te zijn
Milieuvernuft:deze creatieve zakelijke ideeën zijn bedoeld om zowel duurzaam als succesvol te zijn De pandemie 's nachts zien:hoe satellieten meer waarnemen dan alleen het weer
De pandemie 's nachts zien:hoe satellieten meer waarnemen dan alleen het weer Witte Huis verandert van koers, steunt push voor $ 200 miljoen aan Everglades-financiering
Witte Huis verandert van koers, steunt push voor $ 200 miljoen aan Everglades-financiering Oude schedel die waarschijnlijk toebehoort aan 's werelds oudste tsunami-slachtoffer
Oude schedel die waarschijnlijk toebehoort aan 's werelds oudste tsunami-slachtoffer
Hoofdlijnen
- Middelgrote carnivoren lopen het grootste risico door veranderingen in het milieu
- Verontwaardiging na koala gevonden vastgeschroefd aan paal in Australië
- Keizerspinguïns kunnen record snel inkorten door te snacken
- Baby bongo geboren, waarschijnlijk binnenkort in Species Survival Center
- Studie geeft inzicht in hoe algen kooldioxide uit de lucht zuigen
- Hoe zijn genen, DNA en chromosomen met elkaar verbonden?
- Californische condors keren terug naar de lucht na bijna uitsterven
- Wat is het belang van virtual reality voor artsen en chirurgen?
- Olifantenstroperij in Afrika neemt af, maar ivoorvangsten nemen toe:studie
 Life Cycle of a Dragonfly
Life Cycle of a Dragonfly Perth in Australië bestrijdt bosbrand te midden van virusvergrendeling
Perth in Australië bestrijdt bosbrand te midden van virusvergrendeling Spreken met neuronen:nieuwe nanogestructureerde neurale elektroden
Spreken met neuronen:nieuwe nanogestructureerde neurale elektroden Schilderen met licht:nieuwe nanopilaren regelen nauwkeurig de intensiteit van doorvallend licht
Schilderen met licht:nieuwe nanopilaren regelen nauwkeurig de intensiteit van doorvallend licht Hoe Iron
Hoe Iron Onderzoekers ontwikkelen een nieuw model voor de uitstoot van bosbranden
Onderzoekers ontwikkelen een nieuw model voor de uitstoot van bosbranden Berekeningsanalyse ontrafelt het complexe gedrag van een polymeer
Berekeningsanalyse ontrafelt het complexe gedrag van een polymeer Wetenschappers werpen nieuw licht op de mysterieuze oorsprong van ultra-hoge-energetische kosmische straling-hotspot
Wetenschappers werpen nieuw licht op de mysterieuze oorsprong van ultra-hoge-energetische kosmische straling-hotspot
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com