
Wetenschap
Aan de rand van chaos:nieuwe methode voor analyse van stabiliteit van exoplaneten
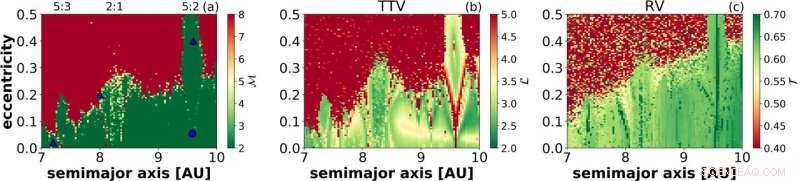
Een stabiliteitskaart van Saturnus verkregen door chaos-indicator MEGNO (a) en herhalingsnetwerk meet de gemiddelde padlengte (b) en transitiviteit (c). De laatste twee panelen zijn gebaseerd op de transittimingvariatie van Jupiter en de radiale snelheid van de zon, respectievelijk. Krediet:Tamás Kovács
Exoplaneten die rond verre sterren draaien, worden snel scherpgesteld met geavanceerde technologie zoals de Kepler-ruimtetelescoop. Het is moeilijk om deze systemen volledig te begrijpen, omdat de beginposities en snelheden van de exoplaneten onbekend zijn. Bepalen of de systeemdynamiek quasi-periodiek of chaotisch is, is omslachtig, duur en rekenkundig veeleisend.
In deze week Chaos , Tamás Kovács levert een alternatieve methode voor stabiliteitsanalyse van exoplanetaire lichamen waarbij alleen de waargenomen tijdreeksgegevens worden gebruikt om dynamische metingen af te leiden en de onvoorspelbaarheid van exoplaneetsystemen te kwantificeren.
"Als we de heersende vergelijkingen van de beweging van een systeem niet kennen, en we hebben alleen de tijdreeksen - wat we meten met de telescoop - dan willen we die tijdreeksen omzetten in een complex netwerk. In dit geval, het wordt een herhalingsnetwerk genoemd, "Zei Kovács. "Dit netwerk bevat alle dynamische kenmerken van het onderliggende systeem dat we willen analyseren."
Het artikel is gebaseerd op het werk van natuurkundige Floris Takens, die in 1981 voorstelde dat de dynamiek van een systeem kon worden gereconstrueerd met behulp van een reeks observaties over de toestand van het systeem. Met de inbeddingsstelling van Takens als uitgangspunt, Kovács gebruikt tijdvertragingsinbedding om een hoogdimensionaal traject te reconstrueren en vervolgens herhalingspunten te identificeren, waar lichamen in de faseruimte dicht bij elkaar liggen.
"Die speciale punten zullen de hoekpunten en de randen van het complexe netwerk zijn, " zei Kovács. "Als je eenmaal het netwerk hebt, u kunt dit netwerk herprogrammeren om maatregelen als transitiviteit, gemiddelde padlengte of andere die uniek zijn voor dat netwerk."
Kovács test de betrouwbaarheid van de methode met een bekend systeem als model, het drielichamenstelsel van Saturnus, Jupiter en de zon, en past het vervolgens toe op het Kepler 36b- en 36c-systeem. Zijn Kepler-systeemresultaten komen overeen met wat bekend is.
"Eerdere studies wezen uit dat Kepler 36b en 36c een heel speciaal systeem is, omdat uit de directe simulatie en de numerieke integraties, we zien dat het systeem aan de rand van de chaos staat, " zei Kovács. "Soms, het vertoont een regelmatige dynamiek, en op andere momenten het lijkt chaotisch."
De auteur is van plan zijn methoden vervolgens toe te passen op systemen met meer dan drie lichamen, het testen van de schaalbaarheid en het verkennen van het vermogen om langere tijdreeksen en scherpere datasets aan te kunnen.
 3D-geprint voedsel opscheppen, één smakelijke afdruk per keer
3D-geprint voedsel opscheppen, één smakelijke afdruk per keer Snel, betrouwbare test voor besmetting met micro-organismen
Snel, betrouwbare test voor besmetting met micro-organismen Een nieuwe tool om eiwitten aan en uit te zetten
Een nieuwe tool om eiwitten aan en uit te zetten Röntgenlaseronderzoek identificeert kristallijn tussenproduct in onze weg naar ademen
Röntgenlaseronderzoek identificeert kristallijn tussenproduct in onze weg naar ademen Onderzoek naar de effecten van vocht en drogen op cement
Onderzoek naar de effecten van vocht en drogen op cement
 Interessante feiten over stranden
Interessante feiten over stranden  De houding ten opzichte van wonen met een gemiddelde dichtheid verandert in Sydney en Melbourne
De houding ten opzichte van wonen met een gemiddelde dichtheid verandert in Sydney en Melbourne Klimaatactiepotentiaal in afvalverbrandingsinstallaties
Klimaatactiepotentiaal in afvalverbrandingsinstallaties Stedelijke groei, hitte eilanden, vochtigheid, klimaatverandering:kosten vermenigvuldigen in tropische steden
Stedelijke groei, hitte eilanden, vochtigheid, klimaatverandering:kosten vermenigvuldigen in tropische steden Wetenschappers gebruiken satellieten om essentiële ondergrondse watervoorraden te meten
Wetenschappers gebruiken satellieten om essentiële ondergrondse watervoorraden te meten
Hoofdlijnen
- Microbiële bewoner stelt kevers in staat zich te voeden met een bladdieet
- De vierkantswortel vinden op een Texas Instrument TI-30X IIS
- Gevaren van het inademen van olierook
- Gletsjermuizen bewegen en dat heeft wetenschappers versteld doen staan
- Wat is de functie van aerobe ademhaling?
- Acht jaar durend onderzoek levert een verhandeling op over lintwormen en honderden nieuwe soorten
- Knoflook kan chronische infecties bestrijden
- RNA (ribonucleïnezuur): definitie, functie, structuur
- nieuwe wegen, betere biobrandstoffen
- Remora-geïnspireerde zuigschijf bootst het hechtingsvermogen van vissen na, biedt evolutionair inzicht

- Wetenschappers horen twee atomen chatten

- Natuurwetten vervangen vallen en opstaan in nieuwe benaderingen van bioprinten
- Onaangenaam achtergrondlicht helpt de kalibratie van de ruimtelijke lichtmodulator te bevorderen
- Wetenschappers ontdekken nieuwe staat van materie

 Injecteerbaar nanonetwerk regelt de bloedsuikerspiegel bij diabetici dagenlang
Injecteerbaar nanonetwerk regelt de bloedsuikerspiegel bij diabetici dagenlang Onderzoeker:gegevens over 267 miljoen Facebook-gebruikers blootgesteld
Onderzoeker:gegevens over 267 miljoen Facebook-gebruikers blootgesteld ATLAS Experiment bestudeert de dynamiek van top-quarks met een zeer hoog momentum
ATLAS Experiment bestudeert de dynamiek van top-quarks met een zeer hoog momentum Met atoommuziek kunnen luisteraars de atomaire wereld ervaren door middel van geluid
Met atoommuziek kunnen luisteraars de atomaire wereld ervaren door middel van geluid Booreilanden kunnen uitstoot onder de Noordzee pompen
Booreilanden kunnen uitstoot onder de Noordzee pompen NASA vindt nieuw gevormde tropische storm Dahlia die vecht tegen windschering
NASA vindt nieuw gevormde tropische storm Dahlia die vecht tegen windschering Graft- en veiligheidskwesties voeden de handel in het verleden van Irak
Graft- en veiligheidskwesties voeden de handel in het verleden van Irak Het cultiveren van de verbindingen tussen mensen en hun omgeving
Het cultiveren van de verbindingen tussen mensen en hun omgeving
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | German | Dutch | Norway | Swedish | Danish |

-
Wetenschap © https://nl.scienceaq.com

