
Wetenschap
De fysieke limiet van kwantumoptica lost een mysterie van computationele complexiteit op
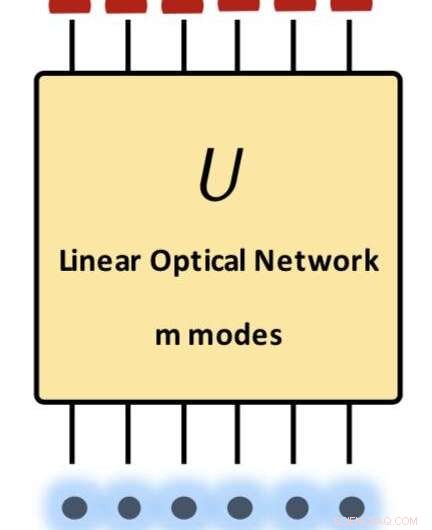
Samenvatting van ons belangrijkste resultaat:een bovengrens van de overgangsamplitudes voor lineaire optica. De begin- en eindtoestanden zijn producten van Fock-staten. De matrix U presenteert elke realiseerbare unitaire transformatie in lineaire optica. Krediet:Science China Press
Lineaire optica is een van de beste voorbeelden voor het demonstreren van kwantumfysica. Het werkt bij kamertemperatuur, en kan worden waargenomen met relatief eenvoudige apparaten. Lineaire optica omvat fysieke processen die het totale aantal fotonen behouden. In het ideale geval, als er aan het begin 100 fotonen zijn, hoe ingewikkeld het fysieke proces ook is, uiteindelijk blijven er precies 100 fotonen over.
Fotonen zijn bosonische niet-interagerende deeltjes. Echter, ze kunnen nog steeds met elkaar interfereren, niet-triviale kwantumeffecten vertonen. Een typisch voorbeeld is het Hong-Ou-Mandel-experiment, waarbij twee identieke fotonen naar een experimenteel apparaat worden gestuurd. Na een eenvoudige lineaire transformatie, de twee fotonen zien eruit alsof ze aan elkaar vast zitten en niet willen scheiden. Naast het verschaffen van een fundamenteel begrip van de kwantummechanica, de studie van lineaire optica heeft ook geleid tot veel wetenschappelijke toepassingen.
In recente jaren, de unieke eigenschappen van lineaire optische systemen hebben ook de ontwikkeling van computationele complexiteitstheorie geïnspireerd. In 2012, Professor Scott Aaronson van het MIT (momenteel aan de Universiteit van Texas in Austin) stelde een lineaire optische methode voor om de kwantum (computationele) suprematie aan te tonen, die is gebaseerd op het concept van boson-bemonstering. Specifieker, Aaronson suggereerde dat voor een klasse van bemonsteringsproblemen gebaseerd op lineaire optische systemen, het zou in de praktijk onmogelijk zijn om een klassieke computer toe te passen om te simuleren. Dit idee leidt onmiddellijk tot een race om de status van 'kwantum suprematie' te bereiken. Veel optische kwantumlaboratoria over de hele wereld zijn geïnteresseerd geraakt in het ontwikkelen van boson-bemonsteringssystemen om records te breken in termen van fotonaantallen. Anderzijds, computerwetenschappers zijn bezig met het toepassen van supercomputers om de lat hoger te leggen voor het bereiken van quantum suprematie.
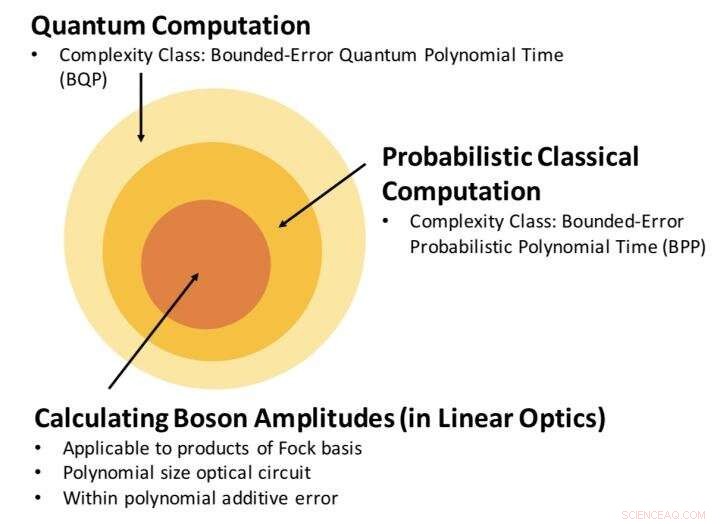
Relatie tussen van de complexiteitsklasse van het schatten van bosonamplitude, en klassieke en kwantumberekening. Ons resultaat stelt vast dat het berekenen van de bosonamplitude, met een polynoom additieve fout, is een probleem binnen BPP. Krediet:Science China Press
Echter, wat betreft praktische problemen, het toepassen van het model van bosonbemonstering is geen goede benadering. Daarom, Aaronson stelde in 2012 een vraag:afgezien van steekproefproblemen, kunnen onderzoekers lineaire optica gebruiken om kwantumsuprematie te bereiken in termen van beslissingsproblemen met een JA/NEE-antwoord? Onlangs, Prof. Man-Hong Yung, universitair hoofddocent van SUSTech en zijn collega's publiceerden een paper met de titel "Universal bound on sampling bosons in linear optics and its computational Implicaties" in Nationale wetenschappelijke recensie ( NSR ), het aanbieden van een complete oplossing voor het openstaande probleem van Aaronson.
specifiek, Yung's team ontdekte een fundamentele limiet op de overgangskansen van lineaire optische systemen, beperking van de mogelijkheid om bosonen over te dragen met behulp van lineaire optische apparaten. Samen met de instrumenten van kwantumoptica, ze ontwikkelden een klassiek algoritme dat de overgangsamplitude efficiënt kan schatten met een begrensde fout. Bijgevolg, deze resultaten leiden tot een negatief antwoord op het open probleem van Aaronson. Met andere woorden, voor het coderen van moeilijke beslissingsproblemen, het is noodzakelijk om gebruik te maken van meer gecompliceerde kwantumoptica-systemen in plaats van alleen lineaire optica.
Als interdisciplinair domein tussen kwantumfysica en informatica, kwantuminformatiewetenschap blijft een zeer actief onderzoeksgebied. Aan de ene kant, de resultaten van Yung's team dragen bij aan de theoretische basis van kwantumoptica; anderzijds, naast bosonbemonstering, deze resultaten wijzen op een nieuw perspectief op computationele complexiteitsproblemen in termen van kwantumoptica. Ongetwijfeld, in de toekomst, we zouden op dit gebied nog veel meer opwindende resultaten zoals deze mogen verwachten.
 Omhulsels drijven krachtige nieuwe kunstmatige spieren aan
Omhulsels drijven krachtige nieuwe kunstmatige spieren aan Bio-geïnspireerde hydrogel kan snel overschakelen naar hard plastic
Bio-geïnspireerde hydrogel kan snel overschakelen naar hard plastic Een op uranium gebaseerde verbinding verbetert de productie van stikstofproducten
Een op uranium gebaseerde verbinding verbetert de productie van stikstofproducten Hoe kunnen chloorfluorkoolwaterstoffen schadelijk zijn voor de ozonlaag?
Hoe kunnen chloorfluorkoolwaterstoffen schadelijk zijn voor de ozonlaag?  Elementen kunnen tegelijkertijd vast en vloeibaar zijn, studie onthult
Elementen kunnen tegelijkertijd vast en vloeibaar zijn, studie onthult
Hoofdlijnen
- De effecten van tornado's op mens en natuur
- Robotapparaat volgt plantengroei op cellulair niveau
- Soorten organismen die van plantencellen zijn gemaakt
- Schimmelmicroben als biomeststoffen in landbouw en tuinieren:is de beloning groter dan het risico?
- 'S Werelds oudste bevroren sperma werkt prima
- Zit moraliteit in de hersenen?
- Nieuwe studie geeft aan hoe bevruchting veranderingen teweegbrengt in duizenden eiwitten in kikkereieren
- Studie vindt verband tussen ontbossing en visserijopbrengsten in de Amazone
- Music Science Fair Project Ideas
- Updaten van het Turings-model van patroonvorming

- Nieuw algoritme verbetert de reconstructie van ptychografische afbeeldingen

- Fermilab-wetenschappers gaan op zoek naar donkere materie met behulp van kwantumtechnologie

- Volgcellen met omnidirectionele zichtbare laserdeeltjes
- Natuurkundigen vinden bewijs van voorheen onzichtbare overgang in ferro-elektriciteit

 Een bier dat echt niet van deze wereld is
Een bier dat echt niet van deze wereld is Israëlische archeologen beweren de oude stad te hebben ontdekt
Israëlische archeologen beweren de oude stad te hebben ontdekt Wetenschappers gebruiken eigen cellen en materialen van patiënten om volledig gepersonaliseerde weefselimplantaten van welke aard dan ook te maken
Wetenschappers gebruiken eigen cellen en materialen van patiënten om volledig gepersonaliseerde weefselimplantaten van welke aard dan ook te maken Onderzoekers tonen aan dat zelfsteriliserende polymeren werken tegen SARS-CoV-2
Onderzoekers tonen aan dat zelfsteriliserende polymeren werken tegen SARS-CoV-2 Influencers belangrijk in coronaviruscommunicatie
Influencers belangrijk in coronaviruscommunicatie 's Werelds eerste productie van aluminium scandiumnitride via MOCVD
's Werelds eerste productie van aluminium scandiumnitride via MOCVD Hoe een negatieve noemer in een positief te veranderen
Hoe een negatieve noemer in een positief te veranderen Hoe kun je honingbijen trainen om naar bommen te snuiven?
Hoe kun je honingbijen trainen om naar bommen te snuiven?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

