
Wetenschap
Wetenschappers ontdekken meer dan 600 nieuwe periodieke banen van het beroemde drielichamenprobleem
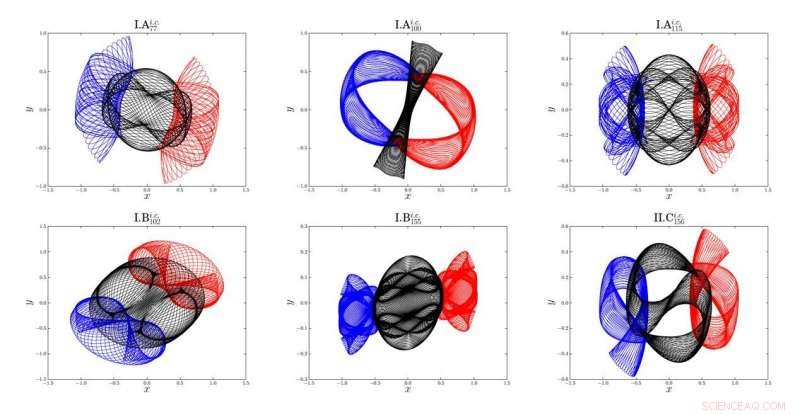
Kort overzicht van de zes nieuw ontdekte families van periodieke banen met drie lichamen. Blauwe lijn:baan van Body-1; rode lijn:baan van Body-2; zwarte lijn:baan van Body-3 Credit:©Science China Press
Het beroemde drielichamenprobleem is terug te voeren op Isaac Newton in de jaren 1680. Onderzoek naar het drielichamenprobleem leidde tot de ontdekking van de zogenaamde gevoeligheidsafhankelijkheid van de beginconditie (SDIC) van chaotische dynamische systemen. Vandaag, chaotische dynamiek wordt algemeen beschouwd als de derde grote wetenschappelijke revolutie in de natuurkunde in de 20e eeuw, vergelijkbaar met relativiteit en kwantummechanica. Dus, studies over het drielichamenprobleem hebben een zeer belangrijke wetenschappelijke betekenis.
in 1890, Poincare stelde vast dat trajecten van drielichamensystemen gewoonlijk niet-periodiek zijn, d.w.z. niet herhalen. Dit kan verklaren waarom het zo moeilijk is om de periodieke banen van drielichamenstelsels te verkrijgen. In de 300 jaar sinds het drielichamenprobleem voor het eerst werd erkend, slechts drie families van periodieke banen waren gevonden. In 2013, Suvakov en Dmitrasinovic [ Fys. ds. Lett. 110, 114301 (2013)] maakte een doorbraak, het vinden van 13 nieuwe afzonderlijke periodieke banen die behoren tot 11 nieuwe families van het Newtoniaanse vlakke drielichamenprobleem met gelijke massa en nul impulsmoment. Nutsvoorzieningen, twee wetenschappers, XiaoMing Li en ShiJun Liao aan de Shanghai Jiaotong University, China, hebben met succes 695 families van periodieke banen van hetzelfde Newtoniaanse vlakke drielichamensysteem bepaald met behulp van de TH-2 supercomputer in Guangzhou, China. Hun resultaten zijn gepubliceerd in WETENSCHAP CHINA-Natuurkunde Mechanica &Astronomie . Video's van deze banen zijn hier beschikbaar.
Deze 695 periodieke banen omvatten de bekende 8-familie gevonden door Moore in 1993, de 11 families gevonden door Suvakov en Dmitrasinovic in 2013, en meer dan 600 nieuwe gezinnen meldden zich voor het eerst. De twee wetenschappers gebruikten de zogenaamde schone numerieke simulatie (CNS), een nieuwe numerieke strategie voor betrouwbare simulaties van chaotische dynamische systemen voorgesteld door de tweede auteur in 2009, die is gebaseerd op een hoge orde van Taylor-reeksen en meerdere precisiegegevens, plus een convergentie/betrouwbaarheidscontrole. Het CNS kan afkapfouten en afrondingsfouten zo effectief verminderen dat numerieke ruis verwaarloosbaar is gedurende een voldoende lange tijdsinterval, dus meer periodieke banen van het drielichamensysteem kunnen worden verkregen.
Zoals gemeld door Montgomery in 1998, elke periodieke baan in de reële ruimte van het drielichamensysteem komt overeen met een gesloten curve op de zogenaamde "vormbol, " die wordt gekenmerkt door zijn topologie met behulp van het zogenaamde "vrije groepselement". De gemiddelde periode van een baan is gelijk aan de periode van de baan gedeeld door de lengte van het overeenkomstige vrije groepselement. Deze 695 families suggereren dat het vierkant van de gemiddelde periode maal de derde macht van de totale kinetische en potentiële energie is ongeveer gelijk aan een constante.De gegeneraliseerde derde wet van Kepler onthult dat het drielichamensysteem iets gemeen heeft dat het begrip van het drielichamensysteem zou kunnen verdiepen.
Volgens de wetenschappers de ontdekking van de meer dan 600 nieuwe periodieke banen is voornamelijk te danken aan de vooruitgang in de informatica en het gebruik van de nieuwe strategie van numerieke simulatie voor chaotische dynamische systemen, namelijk het CZS. Benadrukt moet worden dat via het CZS nog 243 nieuwe periodieke banen van het drielichamenstelsel worden gevonden. Met andere woorden, als traditionele algoritmen met dubbele precisie werden gebruikt, ongeveer 40 procent van de nieuwe periodieke banen zou verloren gaan. Dit geeft de nieuwheid en originaliteit van het CZS aan, aangezien elke nieuwe methode iets nieuws moet bieden.
 Onderzoekers onthullen sensor die COVID-19-infectie snel detecteert
Onderzoekers onthullen sensor die COVID-19-infectie snel detecteert Stabilisatie van het borafluoreen-anion met carbenen
Stabilisatie van het borafluoreen-anion met carbenen Team gedecodeerd moleculair mechanisme dat zwermmotiliteit van bacteriële populaties remt
Team gedecodeerd moleculair mechanisme dat zwermmotiliteit van bacteriële populaties remt Supercomputing bootst berkelium-experimenten na om nieuwe vondst te valideren
Supercomputing bootst berkelium-experimenten na om nieuwe vondst te valideren Efficiënte en high-throughput techniek om de structuur van DNA te bestuderen
Efficiënte en high-throughput techniek om de structuur van DNA te bestuderen
 Hoe een Paper Hornets Nest
Hoe een Paper Hornets Nest  Methaan-etende microben kunnen de uitstoot van gassen verminderen als de Antarctische ijskappen smelten
Methaan-etende microben kunnen de uitstoot van gassen verminderen als de Antarctische ijskappen smelten Wat zijn de verschillende soorten kreeften?
Wat zijn de verschillende soorten kreeften?  Onderzoekers creëren nieuwe routekaart voor het berekenen van de maatschappelijke kosten van koolstof
Onderzoekers creëren nieuwe routekaart voor het berekenen van de maatschappelijke kosten van koolstof De negatieve effecten op het milieu door Maple Syrup
De negatieve effecten op het milieu door Maple Syrup
Hoofdlijnen
- Manieren om te voorkomen dat studenten mobiele telefoons gebruiken in Class
- Het verschil van de genomische DNA-extractie tussen dier en plant
- Chimpansees en roetzwarte mangabeys verstoren de relaties van andere groepsleden
- Eiwit-overexpressieprotocol
- 10 tips van gelukkige mensen
- Hoe vergelijk ik Frankenstein & Cloning?
- Amerikaanse eiken delen een gemeenschappelijke noordelijke voorouder
- RNA-mutatie vs. DNA-mutatie
- Wat is het Genotype voor de Roan-kleur?
- Simulaties demonstreren ionenverwarming door plasmaoscillaties voor fusie-energie
- Niet-invasieve beeldvormingstechniek kan de noodzaak voor herhaalde kankeroperaties verminderen

- De potentiële voorboden van nieuwe fysica blijven bestaan in LHC-gegevens

- Terwijl vogels fluiten, plasma zou niet moeten:nieuw inzicht kan fusie-energie bevorderen

- Elektronische kaart onthult verkeersregels in supergeleider
 Onderzoekers stellen kristalstructuur van maagprotonpomp vast
Onderzoekers stellen kristalstructuur van maagprotonpomp vast Broeikasgasemissies uit reservoirs hoger dan eerder verwacht
Broeikasgasemissies uit reservoirs hoger dan eerder verwacht Hoe variëren hoogfrequente oscillaties van tropische cyclonen in de W North Pacific?
Hoe variëren hoogfrequente oscillaties van tropische cyclonen in de W North Pacific? Nieuwe innovatieve statistische tool verbetert de bestrijding van vervuiling in steden
Nieuwe innovatieve statistische tool verbetert de bestrijding van vervuiling in steden Zonne-energie gebruiken om gemeenschappen te verlichten, de inkomens van plattelandshuishoudens laten groeien
Zonne-energie gebruiken om gemeenschappen te verlichten, de inkomens van plattelandshuishoudens laten groeien Hoe River Rocks Roteren
Hoe River Rocks Roteren  Een tractor vullen Tyre
Een tractor vullen Tyre De geheimen van donkere materie ontsluiten
De geheimen van donkere materie ontsluiten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

