
Wetenschap
Nooit eerder vertoonde topologische solitonen experimenteel gerealiseerd in vloeibare kristallen
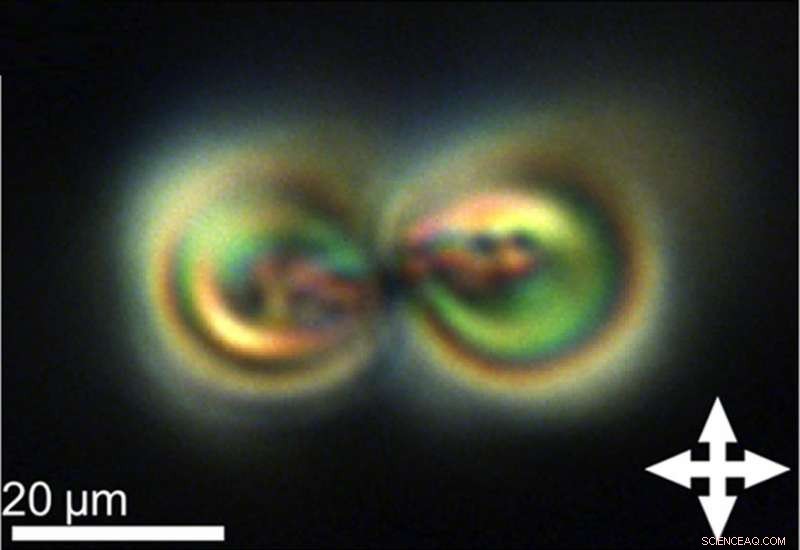
Een polariserende optische microfoto van de twistion, een soort topologische soliton, waargenomen in chirale nematische vloeibare kristallen. Krediet:Ackerman en Smalyukh. Uitgegeven door de American Physical Society
(Phys.org) — Natuurkundigen hebben ontdekt dat tientallen 3D-geknoopte structuren die 'topologische solitonen' worden genoemd, " die honderden jaren experimenteel ongrijpbaar zijn gebleven, kunnen worden gemaakt en gedurende lange tijd worden ingevroren in vloeibare kristallen zoals die worden gebruikt in elektronische displays. Tot nu, topologische solitonen zijn slechts in enkele experimenten gerealiseerd, en voor zo'n korte tijd dat het onmogelijk was ze in detail te bestuderen.
De nieuwe resultaten kunnen dat allemaal veranderen, omdat ze een manier bieden om een grote diversiteit aan langdurige topologische solitonen te produceren die met microscopen kunnen worden bestudeerd en, misschien ooit, een rol spelen in nieuwe optische en elektrische toepassingen.
De onderzoekers, Paul J. Ackerman en Ivan I. Smalyukh aan de Universiteit van Colorado, Kei, hebben een artikel gepubliceerd over de experimentele realisatie van topologische solitonen in een recent nummer van Fysieke beoordeling X .
"Ons werk stelt experimentele en numerieke benaderingen vast voor gedetailleerde studies van 3D-topologische solitonen, met het grote voordeel een directe vergelijking tussen experimentele en theoretische resultaten mogelijk te maken en met een potentiële impact op vele takken van de natuurkunde en het wiskundige veld van de topologie, " vertelde Smalyukh Phys.org . "Ons werk demonstreert niet alleen experimenteel 3D-topologische solitonen die wiskundigen en theoretische fysici eerder voorzagen, maar onthult ook een reeks solitaire structuren die niet zijn voorzien."
Geknoopte achtergrond
Interesse in topologische solitonen dateert uit het begin van de 19e eeuw, toen de wiskundige Carl Friedrich Gauss suggereerde dat de lijnen van magnetische en elektrische velden 3D-knopen vormen die zich als deeltjes zouden kunnen gedragen. Later, Lord Kelvin en anderen beschouwden geknoopte wervels als een vroeg model van het atoom, waarin de eigenschappen van de knopen de chemische eigenschappen van de verschillende elementen zouden kunnen verklaren.
Momenteel, veel modellen in de natuurkunde en kosmologie hebben betrekking op topologische solitonen, bijvoorbeeld modellen van systemen van gecondenseerde materie, elementaire deeltjes, magnetische monopolen, en magnetische deeltjes genaamd skyrmionen die een rol spelen in het opkomende gebied van spintronica.
Wat zijn topologische solitonen precies? Als je twee of meer ronde ringen neemt, koppel ze aan elkaar om een ketting te maken, vervorm vervolgens de ringen door eraan te draaien en eraan te trekken alsof ze van stopverf zijn gemaakt, en tenslotte de hele structuur insluiten in een achtergrondoppervlak, het resultaat zou eruitzien als een topologische soliton. Om deze objecten in meer detail te beschrijven, moeten ze worden gedefinieerd als vierdimensionale objecten die "drie bollen, " en deze vierdimensionale objecten vervolgens om te zetten in driedimensionale objecten met behulp van een wiskundige techniek genaamd Hopf-mapping. Het zijn deze 3D-objecten, genaamd "voorbeelden, " dat zijn de gekoppelde ringen die worden weergegeven in visuele voorstellingen.
Een van de redenen waarom topologische solitonen zo moeilijk experimenteel te realiseren zijn, is dat ze overeenkomen met de laagste energietoestand van een fysiek systeem om stabiel te zijn. Om deze reden, ze zijn alleen aangetoond als tijdelijke structuren in vloeibare kristallen. Het is ook mogelijk dat topologische solitonen bestaan in een ander medium, chirale ferromagneten, maar een gebrek aan experimentele beeldvormingstechnieken verhindert onderzoekers om ze te observeren.
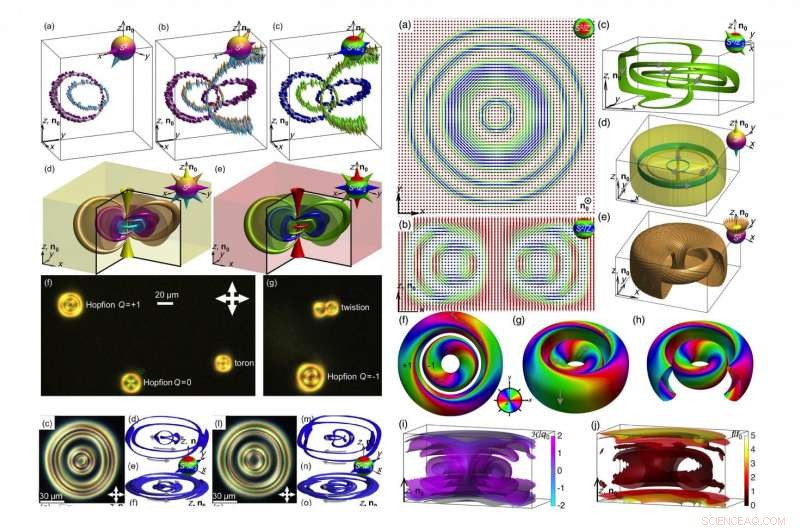
Een assortiment van topologische solitonen, weergegeven door computersimulaties, illustraties van Hopf-kaarten, en polariserende optische microfoto's. Krediet:Ackerman en Smalyukh. Uitgegeven door de American Physical Society
Bevriezende knopen
In de nieuwe studie de onderzoekers ontwikkelden een methode om topologische solitonen in een vaste film van chirale nematische vloeibare kristallen te "bevriezen" door een polymerisatieproces met lage niveaus van ultraviolet licht, samen met verwarming en koeling. Om het experiment breed toegankelijk te maken, de onderzoekers gebruikten in de handel verkrijgbare vloeibare kristallen, waaraan ze chirale doteermiddelen hebben toegevoegd. Optisch pincet gebruiken om patronen in de voorgevroren vloeibare kristallen te genereren en te manipuleren, de onderzoekers konden ook de soorten topologische solitonen controleren die worden gemaakt.
Nadat de topologische solitonen in de vloeibare kristallen zijn bevroren, de onderzoekers kunnen ze bestuderen met behulp van een optische microscoop, in het bijzonder, een drie-foton excitatie fluorescentie polariserende microscoop, die een optisch signaal produceert dat kan worden gebruikt om 3D-beelden van de solitonen te construeren.
In het tweede deel van hun studie, de onderzoekers lieten zien hoe deze gegevens vervolgens kunnen worden gebruikt om numerieke simulaties te maken die overeenkomen met de zeer complexe fysieke structuren. Dit proces is gebaseerd op het analyseren van de energetisch gunstige draaipatronen die de elastische vrije energie van de vloeibare kristallen minimaliseren. Eigenlijk, dit proces van het omzetten van de experimentele structuren (preimages) naar numerieke modellen is analoog aan de wiskundige Hopf mapping van 3D-objecten (preimages) naar vier dimensies.
Potentiële toepassingen
De mogelijkheid om langdurige topologische solitonen te genereren, opent ook de deuren naar mogelijke toepassingen. Een idee is om te profiteren van het feit dat verschillende topologische solitonen verschillende optische eigenschappen hebben, die kunnen worden gebruikt in optische apparaten die de fase van licht verschuiven, evenals in pixels voor optische displays. In aanvulling, als de topologische solitonen die hier in vloeibare kristallen worden geïdentificeerd ook in vaste ferromagneten voorkomen, de onderzoekers verwachten dat ze mogelijk een revolutie teweeg kunnen brengen in het veld van skyrmionics, waarin skyrmionen kunnen worden gebruikt om magnetische apparaten te bouwen, zoals gegevensopslag en logica.
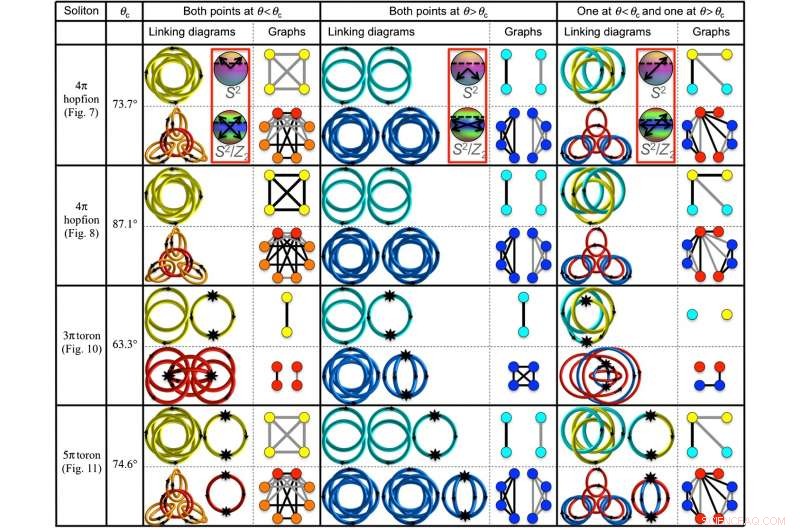
Koppelen van diagrammen en grafieken van enkele 3D-topologische solitonen. Krediet:Ackerman en Smalyukh. Uitgegeven door de American Physical Society
"De grote verscheidenheid aan gelokaliseerde stabiele topologische solitonen op lange termijn, gecombineerd met de unieke elektro-optische eigenschappen van het vloeibare kristalgastheermedium, zal onvermijdelijk leiden tot technologische toepassingen, zoals elektro-optische apparaten en bistabiele informatiedisplays, "Ackerman zei. "Een breed spectrum van nieuwe kansen ontstaat ook aan de fundamentele kant, waar onze onderzoeksgroep zal werken om vast te stellen hoe verschillende topologische solitonen elkaar kunnen transformeren en ook hoe de solitonen met grote Hopf-indexwaarden experimenteel kunnen worden gerealiseerd."
Algemeen, een van de grootste voordelen van de nieuwe methode is dat het een veel uitgebreidere, gedetailleerde analyse van topologische soliton-voorafbeeldingen dan andere constructiemethoden. Als resultaat, de nieuwe methode onthult kleine details in de topologie die anders gemakkelijk over het hoofd zouden kunnen worden gezien, zoals subtiele verschillen tussen zeer vergelijkbare structuren die ten onrechte als dezelfde structuur kunnen worden beschouwd. De resultaten laten zien dat topologische solitonen complexer en diverser zijn dan eerder bewijs kon aantonen, en geven aan dat nog veel meer van deze structuren wachten om ontdekt te worden.
"Er kan potentieel een oneindig groot aantal topologische solitonen bestaan, vooral als we kijken naar verschillende fysieke systemen, ' zei Smalyukh.
© 2017 Fys.org
 Een nieuw proces om metallurgische slakken te recyclen
Een nieuw proces om metallurgische slakken te recyclen Soorten scrubbers
Soorten scrubbers  Onderzoekers gebruiken elektrostatische lading om deeltjes te assembleren tot materialen die edelstenen nabootsen, zout
Onderzoekers gebruiken elektrostatische lading om deeltjes te assembleren tot materialen die edelstenen nabootsen, zout Nieuwe katalyse met één atoom zorgt voor reductieve amineringsreactie
Nieuwe katalyse met één atoom zorgt voor reductieve amineringsreactie Onderzoekers produceren kosteneffectieve, milieuvriendelijk glasmateriaal
Onderzoekers produceren kosteneffectieve, milieuvriendelijk glasmateriaal
 Gebruik van Seawater
Gebruik van Seawater Wetenschappers hebben meer vertrouwen in het projecteren van ENSO-veranderingen onder het broeikaseffect
Wetenschappers hebben meer vertrouwen in het projecteren van ENSO-veranderingen onder het broeikaseffect De natuur is een publiek goed - een plan om het te redden met behulp van particuliere markten komt niet over
De natuur is een publiek goed - een plan om het te redden met behulp van particuliere markten komt niet over Sterke aardbeving in het zuidwesten van Pakistan doodt minstens 23
Sterke aardbeving in het zuidwesten van Pakistan doodt minstens 23 Klimaatverandering maakt oceaangolven krachtiger, dreigt vele kustlijnen te eroderen
Klimaatverandering maakt oceaangolven krachtiger, dreigt vele kustlijnen te eroderen
Hoofdlijnen
- Hoe antibioticagebruik bij dieren bijdraagt aan antibioticaresistentie
- De functie van veel eiwitten blijft onduidelijk
- Insect Compound Eye vs. Human Eye
- Uitbreiding tonijnquota stap achteruit voor instandhouding
- Hebben vogelgezang en menselijke spraak biologische wortels?
- Onderzoekers kijken naar de fruitvlieg om het menselijk brein te begrijpen
- Onderzoekers genereren tomaten met verbeterde antioxiderende eigenschappen door genetische manipulatie
- Soorten instrumenten die worden gebruikt voor het meten van lichaamstemperaturen
- Beperkingen van enzymen gebruikt in Forensic Science
- Wetenschappers maken een beeld van geleidende randen in een veelbelovend 2D-materiaal

- Hoe het Deep Underground Neutrino-experiment zal werken

- Ingenieurs ontwikkelen belangrijke wiskundige formule voor het aansturen van kwantumexperimenten
- Verbetering van de detectiemogelijkheden van diamanten met kwantumeigenschappen

- Afstotende fotonen

 Tegenstanders van NJ offshore windproject vrezen dat turbines uitzicht zullen beïnvloeden, vissen, en toerisme
Tegenstanders van NJ offshore windproject vrezen dat turbines uitzicht zullen beïnvloeden, vissen, en toerisme Wetenschappers verbeteren de nauwkeurigheid van de directionele polarimetrische camera verder
Wetenschappers verbeteren de nauwkeurigheid van de directionele polarimetrische camera verder Wat is zilverlegering?
Wat is zilverlegering?  Afbeelding:Lucy high gain antenne van NASA van dichtbij
Afbeelding:Lucy high gain antenne van NASA van dichtbij Waarom is de trekduif uitgestorven?
Waarom is de trekduif uitgestorven? Een cijfer scrollen in het eerste cijfer
Een cijfer scrollen in het eerste cijfer Piek fosfor is op ons, en afvalwater is waardevolle rommel
Piek fosfor is op ons, en afvalwater is waardevolle rommel Hoe de basis van een kegel te berekenen
Hoe de basis van een kegel te berekenen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

