Wetenschap
Wetenschappers hebben de simulatie van zeer nauwkeurige optische instrumenten vereenvoudigd
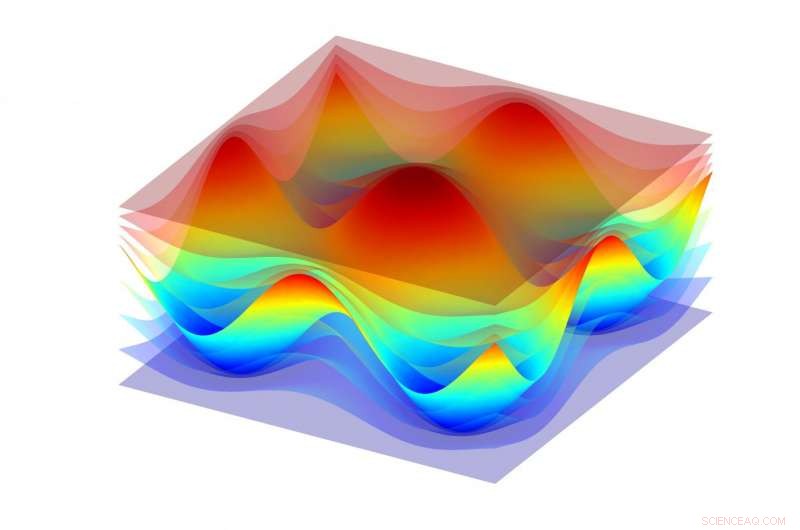
Coördinaatvlakken van een kromlijnig coördinatensysteem geïntroduceerd in een gebied nabij een tweedimensionaal sinusoïdaal diffractierooster zodat een van de vlakken samenvalt met het roosteroppervlak (een ondoorzichtig oppervlak). Krediet:MIPT
Natuurkundigen van het MIPT en de Universiteit Jean Monnet (Frankrijk) hebben een nieuwe simulatiemethode ontwikkeld voor optische elementen die in veel moderne instrumenten en apparaten worden gebruikt. hun papier, het presenteren van een beschrijving van de methode waarmee complexe optische apparaten kunnen worden ontworpen op grafische kaarten voor gaming, is gepubliceerd in de Tijdschrift voor kwantitatieve spectroscopie en stralingsoverdracht .
Alexey Sjtsjerbakov, een medewerker van het Laboratorium voor Nano-optica en Plasmonics bij het Centrum voor Nanoschaal Opto-elektronica van het MIPT, en zijn collega van de Universiteit Jean Monnet Alexandre Tishchenko (1958-2016) stelden een nieuwe benadering voor voor het berekenen van de optische parameters van complexe diffractieroosters en diffractieve elementen. De mogelijkheden van de nieuw ontwikkelde methode zijn aanzienlijk groter dan die van andere veelgebruikte methoden voor een verscheidenheid aan optische structuren. De resultaten van de studie openen nieuwe perspectieven voor de zeer efficiënte optimalisatie van moderne optische en opto-elektronische apparaten.
Diffractieroosters zijn optische elementen die de basis vormen van veel moderne apparaten in spectroscopie, telecommunicatie en lasertechnologieën. Het zijn een- of tweedimensionale periodieke structuren die duizenden regelmatige elementen bevatten, bijv. een reeks parallelle stroken van microscopische breedte. Diffractieroosters zijn in staat om wit licht te splitsen in een spectrum, reflecterende stralen van verschillende golflengten in verschillende richtingen - daarom worden ze in vrijwel alle spectrometers gebruikt.
Een goed voorbeeld van een diffractierooster is een gewone compact disc. Als het wordt verlicht met licht met een vaste frequentie, bijvoorbeeld een rode laserpointer, in plaats van een enkele gereflecteerde straal, een reeks gereflecteerde stralen verschijnt. Dit worden diffractieorders genoemd. De richtingen waarin deze bundels zich voortplanten zijn vast en zijn afhankelijk van de roosterperiode (gedefinieerd als de afstand tussen aangrenzende elementen), de invalshoek, en de stralingsfrequentie. De intensiteit van elke diffractieorde berekenen, d.w.z., de hoeveelheid invallend lichtvermogen dat in elke richting wordt gereflecteerd, is veel moeilijker. Het uitvoeren van dit soort berekeningen met hoge precisie is vanuit praktisch oogpunt uiterst belangrijk, omdat ze essentieel zijn voor de optimalisatie van een breed scala aan instrumenten en apparaten.
Het vermogen van diffractieroosters om licht in een spectrum te splitsen, wordt gebruikt in spectrometers - apparaten die de spectrumanalyse gebruiken om de samenstelling van verschillende stoffen te bepalen, waaronder chemische oplossingen en interstellaire gassen. Diffractiesimulatie is essentieel voor het vervaardigen van lithografiemaskers die worden gebruikt in moderne micro-elektronische fabricage, en voor het ontwerpen van speciale polarisatoren in lasermetaalverwerkingstechnologie. In aanvulling, periodieke structuren worden gebruikt om de efficiëntie van zonneconcentratoren en fotovoltaïsche cellen te verhogen door de lichtabsorptie te verhogen. Periodieke structuren maken het ook moeilijker om documenten en geld te vervalsen - een patroon van fijne metalen stroken op papier die op een bepaalde manier licht reflecteren, kan als vervalsingsmaatregel fungeren.
Een rigoureuze berekening van de efficiëntie van de diffractieorde is alleen mogelijk door de vergelijkingen van Maxwell op te lossen - fundamentele vergelijkingen die het elektromagnetische veld beschrijven en, vooral, elektromagnetische golfvoortplanting. Ze werden meer dan honderd jaar geleden geformuleerd, maar een grote verscheidenheid aan oplossingen die deze vergelijkingen in verschillende gevallen toestaan, motiveert nog steeds veel wetenschappers over de hele wereld om door te gaan met het zoeken naar nieuwe oplossingen. En het beschrijven van complexe optische diffractieroosters met behulp van de vergelijkingen van Maxwell is alleen mogelijk met behulp van numerieke methoden.

Alexey Shcherbakov demonstreert het diffractiepatroon van een tweedimensionaal rooster, tegoed:tegoed:MIPT
Dit betekent dat in plaats van een kant-en-klare formule, een eindige precisie-algoritme moet worden geïmplementeerd. Om complexe diffractieroosters te analyseren en te optimaliseren, onderzoekers gebruiken moderne computers en computerclusters. Een heel wetenschapsgebied dat wiskundige fysica combineert, numerieke analyse, programmeren, en andere gebieden is gewijd aan het onderzoeken hoe computerprogramma's kunnen worden geschreven en hoe deze berekeningen op de meest efficiënte manier kunnen worden uitgevoerd. De ontwikkeling van dit veld wordt gestimuleerd door vooruitgang in fabricagetechnologieën voor diffractiestructuren. Preciezere apparaten stellen steeds hogere eisen aan simulatiemethoden op ontwerpniveau.
In hun publicatie, de onderzoekers ontwikkelden de Generalized Source Method (GSM), het verbruik van computerbronnen aanzienlijk verminderd in vergelijking met andere methoden. Het idee is gebaseerd op hypothetische bronnen van elektromagnetische straling die structurele inhomogeniteit vervangen.
Volgens Alexey Shcherbakov, een senior onderzoeker van het Laboratorium voor Nanooptica, dit idee kan met bepaalde beperkingen, als volgt worden geïllustreerd:"Laten we aannemen dat we stenen in het midden van een cirkelvormige vijver gooien. De golven die door de stenen worden gegenereerd, zullen cirkelvormig zijn en zich vanuit het midden van de vijver naar de waterkant verspreiden. Laten we ons nu afvragen:welke vorm krijgen de golven als er ergens een boot in de vijver drijft? Het blijkt dat als we de boot verwijderen en veel kleine steentjes gooien op de plaats waar hij dreef, deze kleine stenen kunnen zo worden gekozen dat het totale aantal golven dat ze genereren en de steen die we in het midden gooien hetzelfde zal zijn alsof de boot nog in de vijver zou drijven. Deze hypothetische vervanging lijkt de taak misschien te bemoeilijken, maar, in praktijk, dit principe stelt wetenschappers in staat om zeer complexe problemen van golfvoortplanting efficiënt op te lossen."
De kerngedachte van de nieuwe methode op basis van de GSM was het gebruik van kromlijnige coördinatentransformaties in het roostergebied. Binnen de methode rationale, een ruw roosteroppervlak wordt uitgerekt tot een vlak, waardoor het heel eenvoudig is om de reflectie en breking van golven te berekenen. Om de door de ruwheid veroorzaakte fysieke effecten te behouden, moeten bij een dergelijke strekking tegelijkertijd de eigenschappen van de omgeving nabij het oppervlak op een bepaalde manier worden gewijzigd. Dus, in plaats van te worden gereflecteerd op het gegolfde roosteroppervlak, golven lijken door een inhomogene ruimte te gaan, die hun voortplanting op verschillende locaties verschillend vertraagt. Deze techniek verbetert de berekeningen aanzienlijk en verkrijgt veel nauwkeurigere resultaten in dezelfde rekentijd.
Naast de analytische ontwikkeling van de nieuwe aanpak met metrische bronnen, de onderzoekers toonden ook de mogelijkheid aan van efficiënte parallellisatie van de methode en het uitvoeren van simulaties op grafische kaarten. Hierdoor is het mogelijk om met commercieel geproduceerde componenten waarmee alle gamers vertrouwd zijn zeer complexe diffractieroosters te simuleren. De rekenkracht van grafische chips is al groter dan de kracht van processors, daarom worden grafische kaarten in veel laboratoria over de hele wereld gebruikt. In het gepubliceerde onderzoek het vergelijken van simulaties op grafische kaarten en gewone processors toonde aan dat een grafische chip de taak tientallen keren sneller kan doen.
Hoofdlijnen
- Populatie-ecologie: definitie, kenmerken, theorie en voorbeelden
- "3-D Printing Goes Cellular
- Schaatsenrijders illustreren evolutionaire processen
- Ja,
- Hoe werken vaccins met het immuunsysteem?
- Wanneer dupliceren chromosomen tijdens een cellevenscyclus?
- Hebben alle mensen een uniek genotype en fenotype?
- Internationale concurrentiebenchmarks metagenomics-software
- Zes belangrijkste celfuncties
 Een doorbraak in de ontwikkeling van multi-watt terahertz-lasers
Een doorbraak in de ontwikkeling van multi-watt terahertz-lasers WISE1013+6112 is een van de meest lichtgevende infraroodstelsels, studie vondsten
WISE1013+6112 is een van de meest lichtgevende infraroodstelsels, studie vondsten Steden als Lagos hebben bouwontwerpen nodig die niet alleen globale stijlen kopiëren
Steden als Lagos hebben bouwontwerpen nodig die niet alleen globale stijlen kopiëren Hoe werkt koolstofvastlegging?
Hoe werkt koolstofvastlegging?  Schoolprojecten over natuurlijke hulpbronnen
Schoolprojecten over natuurlijke hulpbronnen  Wetenschappers creëren bio-geïnspireerde, breed regelbare ultradunne optische componenten
Wetenschappers creëren bio-geïnspireerde, breed regelbare ultradunne optische componenten Machine learning-systeem kan helpen bij cruciale beslissingen in de zorg voor sepsis
Machine learning-systeem kan helpen bij cruciale beslissingen in de zorg voor sepsis Onderzoekers gebruiken licht van nanodeeltjes om biologische processen te controleren
Onderzoekers gebruiken licht van nanodeeltjes om biologische processen te controleren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com