
Wetenschap
Wat is de pH-waarde van salpeterigzuur?
$$HNO_2 \rightleftharpoenen H^+ + NO_2^-$$
De pH van een zwak zuur kan worden berekend met de volgende formule:
$$pH =-\log[H^+]$$
waarbij [H^+] de waterstofionenconcentratie is in mol per liter (M).
De dissociatieconstante (Ka) voor salpeterigzuur is 4,5 x 10^(-4) bij 25°C. De Ka is een maat voor de sterkte van een zuur, en hoe kleiner de Ka, hoe zwakker het zuur. Voor salpeterigzuur:
$$Ka =[H^+][NO_2^-]/[HNO_2]$$
Aangenomen dat x de concentratie is van H^+- en NO2--ionen die bij evenwicht worden geproduceerd, en de initiële concentratie van HNO2 C is, dan:
$$[H^+] =[NO_2^-] =x$$
$$[HNO_2] =C - x$$
Deze concentraties vervangen door de Ka-expressie:
$$4,5 \maal 10^{−4} =x^2/(C - x)$$
Bij evenwicht is de concentratie van de geconjugeerde base, NO2-, klein vergeleken met de initiële concentratie van HNO2, dus we kunnen aannemen dat C ≈ [HNO2] in de noemer. Daarom, door de vergelijking te vereenvoudigen, hebben we:
$$x^2 + (4,5 \maal 10^{-4})x - (4,5 \maal 10^{-4})C =0$$
Oplossen voor x, de waterstofionenconcentratie:
$$x =\frac{-b ± √(b^2 - 4ac)}{2a}$$
waarbij a =1, b =4,5 x 10^(-4) en c =-(4,5 x 10^(-4))C.
Berekening van de waterstofionenconcentratie (x):
$$x =\frac{-(4,5 \tijden 10^{-4}) ± √((4,5 \tijden 10^{-4})^2 - 4(1)(-4,5 \tijden 10^{-4 })C)}{2(1)}$$
$$x =\frac{4,5 \times 10^{-4} ± 0,0198C}{2}$$
Omdat de waterstofionenconcentratie niet negatief kan zijn, nemen we de positieve wortel:
$$x =\frac{0,0198C + 4,5 \times 10^{-4}}{2}$$
Vervanging van de Ka-expressie in de vergelijking:
$$x =\frac{Ka[HNO_2] + Ka}{2}$$
$$x =\frac{(4,5 \tijden 10^{-4})[HNO_2] + 4,5 \tijden 10^{-4}}{2}$$
Bij 25°C:
$$pH =-\log \left(\frac{(4,5 \times 10^{-4})[HNO_2] + 4,5 \times 10^{-4}}{2}\right)$$
Bijvoorbeeld:
Als [HNO2] =0,1 M:
$$pH =-\log \left(\frac{(4,5 \times 10^{-4})(0,1) + 4,5 \times 10^{-4}}{2}\right) =2,85$$
Daarom is de pH van een 0,1 M salpeterigzuuroplossing ongeveer 2,85.
Hoofdlijnen
- Hoe boeren gebruik maken van wetenschappelijke vooruitgang om zoveel mogelijk biomassa te produceren?
- Wetenschappers bestuderen hoe sperma in een eicel terechtkomt
- Bacteriën met synthetisch gencircuit zelf-assembleren om werkend apparaat te bouwen met gouden nanodeeltjes
- De rommel opruimen:hoe protobiologie ontstond uit prebiotische rommel
- Nieuwe studie ontdekt hoe veranderde eiwitvouwing de meercellige evolutie aandrijft
- Nieuwe vliegsoort in Central Park krijgt bijnaam CCNY-professoren
- Een eerste blik op geografische variatie in ezelspinguïnoproepen
- Hoe klonen werkt
- Nadelen en voordelen van een HPLC
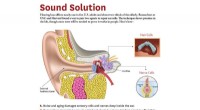
- Het verbinden van hoorhulpmoleculen met het oorbeen
- 's Werelds eerste passieve antivriesoppervlak bestrijdt ijs met ijs

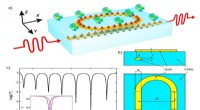
- Bloed en zweet:draagbare medische sensoren krijgen een grote gevoeligheidsboost
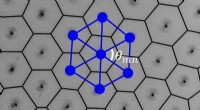
- Onderzoekers creëren actief materiaal uit microscopisch kleine draaiende deeltjes
- Nieuw staal om de levensduur van olieveldpijpleidingen te verdubbelen

 Een techniek om de eerste zwaartekrachtsgolven van het heelal uit te filteren
Een techniek om de eerste zwaartekrachtsgolven van het heelal uit te filteren Hoe een schip in ijs te parkeren
Hoe een schip in ijs te parkeren  Onderzoek onthult hoe verontreinigende stoffen de vroege embryonale ontwikkeling beïnvloeden
Onderzoek onthult hoe verontreinigende stoffen de vroege embryonale ontwikkeling beïnvloeden Multifunctionalisatie van grafeen voor moleculaire gerichte kankertherapie
Multifunctionalisatie van grafeen voor moleculaire gerichte kankertherapie Schrijf een kort essay waarin je een analogie creëert om de beweging van deeltjes te beschrijven. Vergelijk de bewegingen en posities van mensen die dansen met bewegingen van watermoleculen, vloeibaar en in dampvorm?
Schrijf een kort essay waarin je een analogie creëert om de beweging van deeltjes te beschrijven. Vergelijk de bewegingen en posities van mensen die dansen met bewegingen van watermoleculen, vloeibaar en in dampvorm?  Hoe wordt jagerry gemaakt?
Hoe wordt jagerry gemaakt?  Natuur Ph.D. enquête legt de schijnwerpers op geestelijke gezondheid, intimidatie en studieschuld
Natuur Ph.D. enquête legt de schijnwerpers op geestelijke gezondheid, intimidatie en studieschuld Ingenieurs bouwen vloot van autonome boten die van vorm veranderen
Ingenieurs bouwen vloot van autonome boten die van vorm veranderen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


