
Wetenschap
Drie blokken die zijn verbonden door massaloze snaren die langs een horizontale kracht van een wrijvingsloos oppervlak worden getrokken?
Inzicht in de setup
* blokken: Je hebt drie blokken, laten we ze blok 1, blok 2 en blok 3 noemen.
* massa's: Elk blok heeft een massa (M1, M2 en M3).
* strings: De blokken zijn verbonden door massaloze snaren, wat betekent dat de snaren geen massa hebben en geen invloed hebben op de beweging van de blokken.
* Wrijvingsloos oppervlak: De blokken bewegen op een wrijvingsloos oppervlak, wat betekent dat er geen weerstand is tegen hun beweging.
* horizontale kracht: Een horizontale kracht (F) wordt toegepast op een van de blokken (laten we zeggen blok 1).
Analyse van de krachten en beweging
1. Force op blok 1: De kracht F werkt rechtstreeks op blok 1.
2. spanning in string 1: Het string dat blok 1 en blok 2 verbindt, ervaart een spanningskracht (T1). Deze spanningskracht is gelijk in grootte en tegenover de richting van de kracht die blok 1 uitoefent op blok 2.
3. Force op blok 2: Block 2 ervaart de spanningskracht (T1) van de string, die de enige kracht is die erop werkt.
4. spanning in String 2: Het string dat blok 2 en blok 3 verbindt, ervaart een spanningskracht (T2). Deze spanningskracht is gelijk in grootte en tegenover de richting van de kracht die blok 2 uitoefent op blok 3.
5. Force op blok 3: Block 3 ervaart de spanningskracht (T2) uit de string, die de enige kracht is die erop werkt.
Newton's tweede bewegingswet
De tweede bewegingswet van Newton stelt dat de netto kracht die op een object werkt gelijk is aan het product van zijn massa en versnelling (F =MA). We kunnen deze wet op elk blok toepassen:
* Blok 1: F - t1 =m1 * a (waarbij a de versnelling van het hele systeem is)
* Blok 2: T1 - t2 =m2 * a
* Blok 3: T2 =m3 * a
Oplossen voor versnelling en spanning
Om op te lossen voor de versnelling (a) van het systeem en de spanningskrachten (T1 en T2), kunt u de volgende stappen gebruiken:
1. Voeg de vergelijkingen toe: Voeg de drie vergelijkingen samen toe om de spanningskrachten te elimineren. Dit geeft u:f =(m1 + m2 + m3) * a.
2. Oplossen voor versnelling: a =f / (m1 + m2 + m3)
3. Vervang om spanningen te vinden: Vervang de waarde van 'A' terug in een van de drie oorspronkelijke vergelijkingen om op te lossen voor T1 en T2.
Key Points
* Gelijke versnelling: Alle drie de blokken zullen met dezelfde snelheid versnellen (a) omdat ze zijn verbonden door tekenreeksen en als een enkele eenheid worden bewogen.
* massaverdeling: De versnelling van het systeem is omgekeerd evenredig met de totale massa van de drie blokken.
* spanningskrachten: De spanningskrachten in de snaren zullen afhangen van de massa's van de blokken en de uitgeoefende kracht.
Voorbeeld
Laten we zeggen:
* F =10 n
* M1 =2 kg
* M2 =3 kg
* M3 =1 kg
1. Bereken versnelling:A =10 N/(2 kg + 3 kg + 1 kg) =10/6 m/s² ≈ 1,67 m/s²
2. Bereken T1:10 N - T1 =2 kg * (10/6) M/S² => T1 ≈ 6.67 N
3. Bereken t2:t2 =1 kg * (10/6) m/s² ≈ 1,67 n
Samenvattend
Dit systeem laat zien hoe krachten, massa's en versnellingen zijn onderling verbonden in een multi-block-systeem. Door de wetten van Newton toe te passen en de krachten op elk blok zorgvuldig te overwegen, kunt u de versnellings- en spanningskrachten binnen het systeem bepalen.
 Schrijf de moleculaire formule voor water, wat zou de juiste naam dit molecuul zijn als de richtlijnen voor chemische naam van nomenclatuur worden gevolgd?
Schrijf de moleculaire formule voor water, wat zou de juiste naam dit molecuul zijn als de richtlijnen voor chemische naam van nomenclatuur worden gevolgd?  Glow Powder maken van huishoudelijke artikelen
Glow Powder maken van huishoudelijke artikelen Wat is een verandering van vloeistof in benzine?
Wat is een verandering van vloeistof in benzine?  Oprukkende meervoudige legeringen:onderzoekers verkennen nieuwe domeinen van compositorisch complexe metalen
Oprukkende meervoudige legeringen:onderzoekers verkennen nieuwe domeinen van compositorisch complexe metalen Heeft broom de neiging te reageren door elektronen op te nemen?
Heeft broom de neiging te reageren door elektronen op te nemen?
 Plastic ontwerpen om af te breken in de oceaan is mogelijk, maar is het praktisch?
Plastic ontwerpen om af te breken in de oceaan is mogelijk, maar is het praktisch? Wat zijn feiten over de bomen in bladverliezend bos?
Wat zijn feiten over de bomen in bladverliezend bos?  Regelgeving voor kolencentrales verwaarloost een cruciale verontreinigende stof
Regelgeving voor kolencentrales verwaarloost een cruciale verontreinigende stof Hoe is de aardewetenschap gerelateerd aan de echte wereld?
Hoe is de aardewetenschap gerelateerd aan de echte wereld?  Gaat blootstelling binnen de aarde plaats?
Gaat blootstelling binnen de aarde plaats?
Hoofdlijnen
- Wat valideert een hypothese?
- Alle volgende zijn belangrijke eigenschappen Prokaryoten behalve?
- Hoe worden lange DNA-strengen in kleine cellen verpakt?
- Genetische technologie onthult hoe giftige paddenstoelen gifstoffen produceren
- Welke cel leest het DNA tijdens de reproductie?
- Wat maakt clowns zo griezelig?
- Wat zijn de voor- en nadelen van flowcytometrie?
- Wat is een evolutiepatroon waarin twee soorten de relatie tot elkaar evolueren?
- Wat zijn de eigenschappen en functies van hoofdonderdelen een dierencel?
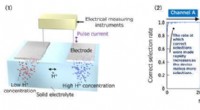
- Ionische beslisser in staat tot zelflerend
- Op zoek naar donkere materie, nieuw fonteinontwerp kan een bron van antwoorden worden
- Qubits met één atoom onder een microscoop bouwen

- Afwijkende kwantumtransportverschijnselen waargenomen in fractale fotonische roosters

- Magnetronlenzen gebruikt voor multi-beam vorming

 Overstroomd Venetië zet zich schrap voor meer overstromingen, harde wind
Overstroomd Venetië zet zich schrap voor meer overstromingen, harde wind Onderzoekers ontwikkelen zachte kleppen om volledig zachte robots te maken
Onderzoekers ontwikkelen zachte kleppen om volledig zachte robots te maken Hoe heet het proces waarbij bomen koolstofdioxide uit de atmosfeer opnemen en zuurstof weer vrijgeven?
Hoe heet het proces waarbij bomen koolstofdioxide uit de atmosfeer opnemen en zuurstof weer vrijgeven?  Tarwegluten gevonden om bindingen in broos mensenhaar te herstellen
Tarwegluten gevonden om bindingen in broos mensenhaar te herstellen Kunnen enzymen de snelheid van chemische reactie verhogen door de energiebarrières van activering te verlagen?
Kunnen enzymen de snelheid van chemische reactie verhogen door de energiebarrières van activering te verlagen?  Life Support handsfree installeren
Life Support handsfree installeren Onderzoekers creëren nanovezel-gusher
Onderzoekers creëren nanovezel-gusher Hoe röntgenstralen hielpen bij het oplossen van het mysterie van drijvende rotsen
Hoe röntgenstralen hielpen bij het oplossen van het mysterie van drijvende rotsen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

