
Wetenschap
In een geïsoleerd systeem botsing twee auto's elk met een massa van 1000 kg. Auto 1 is aanvankelijk in rust, terwijl 2 10 ms bewoog. Ze gaan samen weg. Wat hun snelheid?
Inzicht in behoud van momentum
In een geïsoleerd systeem (waar geen externe krachten handelen) is het totale momentum voordat een botsing gelijk is aan het totale momentum na de botsing.
Momentum -formule
Momentum (P) wordt berekend als:
* p =massa (m) * snelheid (v)
Het probleem oplossen
1. Eerste momentum:
* Auto 1:p1 =(1000 kg) * (0 m/s) =0 kg * m/s
* Auto 2:p2 =(1000 kg) * (10 m/s) =10000 kg * m/s
* Totaal initiële momentum:0 + 10000 =10000 kg* m/s
2. Laatste momentum:
* De twee auto's blijven bij elkaar en vormen een gecombineerde massa van 2000 kg.
* Laat hun laatste snelheid 'V' zijn.
* Totaal laatste momentum:(2000 kg) * (v)
3. Behoud van momentum:
* Eerste momentum =definitief momentum
* 10000 kg * m/s =(2000 kg) * (v)
4. Oplossen voor snelheid (V):
* v =10000 kg* m/s/2000 kg =5 m/s
Antwoord: De snelheid van de twee auto's die samen bewegen na de botsing is 5 m/s.
 Welke eigenschap maakt het solide goed in het uitvoeren van warmte?
Welke eigenschap maakt het solide goed in het uitvoeren van warmte?  Waarom zijn er voor en na de reactie hetzelfde aantal deeltjes?
Waarom zijn er voor en na de reactie hetzelfde aantal deeltjes?  Is fosfor een geleider of is het een isolator?
Is fosfor een geleider of is het een isolator?  Is een suikerkubus chemische verandering op grond?
Is een suikerkubus chemische verandering op grond?  Wat is een uitgebalanceerde chemische vergelijking voor calciumnitraat en natriumsulfaat?
Wat is een uitgebalanceerde chemische vergelijking voor calciumnitraat en natriumsulfaat?
 Waarom storten beschavingen in?
Waarom storten beschavingen in?  Nieuw klimaatmodel helpt onderzoekers waterbehoefte beter te voorspellen
Nieuw klimaatmodel helpt onderzoekers waterbehoefte beter te voorspellen Krachtig, lokale verhalen kunnen ons inspireren om actie te ondernemen tegen klimaatverandering
Krachtig, lokale verhalen kunnen ons inspireren om actie te ondernemen tegen klimaatverandering Studie belicht de resultaten van de wetenschappelijke boringen in het Songliao-bekken
Studie belicht de resultaten van de wetenschappelijke boringen in het Songliao-bekken  Een prijs zetten op koolstofvervuiling alleen zal waarschijnlijk niet helpen om de klimaatdoelen te bereiken
Een prijs zetten op koolstofvervuiling alleen zal waarschijnlijk niet helpen om de klimaatdoelen te bereiken
Hoofdlijnen
- De Filippijnse bioloog en hun bijdragen?
- Kunstmatige intelligentie verbetert de monitoring van bedreigde gemarmerde murrelet
- Walvisontmoetingen in Mexico benadrukken de noodzaak van wereldwijde investeringen in onderzoek naar bultruggen
- Hoe wordt een plant genoemd als deze gewoon begint te groeien?
- Wie heeft de moderne evolutietheorie opgericht?
- Wat doet een menselijke wortel haarcel?
- De hoeveelheid organisch materiaal dat de autotrofe organismen een ecosysteem produceren?
- Wat zijn 5 functies van het skelet?
- Wat is de functie van een transportsysteem in het levende organisme?
- Ga met de stroom mee:nieuwe bevindingen over het verplaatsen van elektriciteit kunnen fusie-apparaten verbeteren

- Onderzoek demonstreert de kwantumversnelling van gesuperviseerd machine learning voor een nieuwe classificatietaak

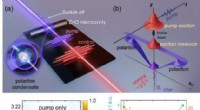
- Een ultrasnelle opto-elektronische schakelaar maken met behulp van een Bose-Einstein-condensaat van polaritonen
- Nieuwe methode maakt onderzoek naar effecten van chemicaliën op DNA mogelijk

- Coherente LiDAR op lange afstand versnellen

 Waarom stort een beetje sneeuw Groot-Brittannië in transportchaos?
Waarom stort een beetje sneeuw Groot-Brittannië in transportchaos? Studie:Milieurisico's verergerd voor kwetsbare bevolkingsgroepen in kleine steden
Studie:Milieurisico's verergerd voor kwetsbare bevolkingsgroepen in kleine steden Welke grondstoffen kunnen worden gebruikt om synthetische diamanten te vervaardigen?
Welke grondstoffen kunnen worden gebruikt om synthetische diamanten te vervaardigen?  Wat is effectief gebruik van energiebetekenis?
Wat is effectief gebruik van energiebetekenis?  Hoe kan Lichen Weather Rock?
Hoe kan Lichen Weather Rock?  Op gadolinium gebaseerde deeltjes tonen en behandelen tumoren
Op gadolinium gebaseerde deeltjes tonen en behandelen tumoren Gaan tulpen overdag open en sluiten de nacht?
Gaan tulpen overdag open en sluiten de nacht?  Fragmenten van energie - geen golven of deeltjes - kunnen de fundamentele bouwstenen van het universum zijn
Fragmenten van energie - geen golven of deeltjes - kunnen de fundamentele bouwstenen van het universum zijn
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

