
Wetenschap
Hoe golflengte beïnvloedt diffractie?
Kortere golflengten =minder diffractie:
* kleinere golflengte: Wanneer lichtgolven een kortere golflengte hebben, hebben ze de neiging om minder te verschillen. Dit komt omdat kortere golflengten minder snel rond obstakels buigen of zich door smalle openingen verspreiden.
* Voorbeeld: Blauw licht heeft een kortere golflengte dan rood licht. Als u beide lichtkleuren door dezelfde smalle spleet schittert, zal het blauwe licht minder verschillen dan het rode licht, wat resulteert in een smaller diffractiepatroon.
langere golflengten =meer diffractie:
* grotere golflengte: Langere golflengtes daarentegen verschillen meer. Ze buigen gemakkelijker rond obstakels en verspreiden zich meer door smalle openingen.
* Voorbeeld: Radiogolven hebben zeer lange golflengten. Dit is de reden waarom radiogolven kunnen verschillen rond gebouwen en heuvels, zodat je radiosignalen kunt ontvangen, zelfs als je niet in een directe gezichtslijn bent met de zender.
De relatie met spleetmaat:
* diffractie is het meest merkbaar wanneer de golflengte van de golf vergelijkbaar is met de grootte van het obstakel of het openen ervan.
* Als de golflengte veel kleiner is dan de opening, gaan de golven bijna ongestoord door, met minimale diffractie.
* Als de golflengte veel groter is dan de opening, verschillen de golven aanzienlijk en verspreiden zich in een breed patroon.
Key Concepts:
* 'Huygens' principe: Dit principe stelt dat elk punt op een golffront kan worden beschouwd als een bron van secundaire wavelets. Deze wavelets interfereren met elkaar, waardoor het waargenomen diffractiepatroon ontstaat.
* diffractierooster: Een diffractierooster is een apparaat met veel dicht bij elkaar geplaatste spleten dat een onderscheidend interferentiepatroon produceert. De afstand van de spleten en de golflengte van het licht bepalen de hoek van de gediffracteerde balken.
Toepassingen:
* holografie: Het creëren van driedimensionale afbeeldingen met behulp van diffractie.
* röntgendiffractie: Gebruikt om de structuur van kristallen en moleculen te bestuderen.
* telescopen: Diffractie beperkt de resolutie van telescopen.
* Microscopie: Diffractie is een sleutelfactor in de resolutielimieten van microscopen.
Samenvattend is golflengte een fundamentele factor in diffractie. Hoe korter de golflengte, hoe minder diffractie optreedt. Deze relatie heeft tal van praktische toepassingen op verschillende wetenschappelijke velden.
 Antarctische wateren:warmer met meer zuurgraad en minder zuurstof
Antarctische wateren:warmer met meer zuurgraad en minder zuurstof Een intense blik op La Brea Tar Pits verklaart waarom we coyotes hebben en geen sabeltandkatten
Een intense blik op La Brea Tar Pits verklaart waarom we coyotes hebben en geen sabeltandkatten  Hoe duurzame gemeenschappen werken
Hoe duurzame gemeenschappen werken  Waarom de druk van ouders het plezier uit het spel van kinderen haalt
Waarom de druk van ouders het plezier uit het spel van kinderen haalt  Feiten over de Atlantische kustvlaktes
Feiten over de Atlantische kustvlaktes
Hoofdlijnen
- Hoeveel organen in totaal heeft een vrouw?
- Hoe zijn organismen manier van leven geroepen?
- Wat doet speeksel het eten?
- Wat zijn enkele nadelen en voordelen om parasiet te zijn?
- Zeg vaarwel tegen knoflookadem met geurvrije zwarte knoflook
- Studie beslecht 125 jaar durend debat over hoe stikstofbindende bacteriën de celwanden van peulvruchten doorbreken
- Wat licht werpen op plantengroei kan betekenen voor kanker
- Wat is het verschil tussen halodurische en halofiele organismen?
- Wat is de eenvoudigste cel?
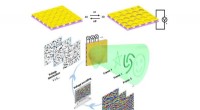
- Herconfigureerbare meta-oppervlakken zorgen voor lichtregeling op nanoschaal
- Skunk Water:een wapen dat stank gebruikt om menigten onder controle te houden

- Op zoek naar het verlichtingsmateriaal van de toekomst

- Het genereren van terahertz-straling uit water maakt het onmogelijke, mogelijk

- Nieuw type atoomklok kan wetenschappers helpen donkere materie te detecteren en het effect van zwaartekracht op tijd te bestuderen

 Smartphone-app kan onthullen hoe stedelijke ruimtes onze gezondheid en welzijn beïnvloeden
Smartphone-app kan onthullen hoe stedelijke ruimtes onze gezondheid en welzijn beïnvloeden Hoeveel mol h zijn er in 2,95 water?
Hoeveel mol h zijn er in 2,95 water?  Elektrolyten kunnen elektriciteit leiden omdat ze er veel bevatten ..?
Elektrolyten kunnen elektriciteit leiden omdat ze er veel bevatten ..?  737 MAX-jet nog minstens 10-12 weken aan de grond:IATA
737 MAX-jet nog minstens 10-12 weken aan de grond:IATA 3D-printen 100 keer sneller met licht
3D-printen 100 keer sneller met licht Waarom zal een gerecht van water bevriezen als er in panalcohol wordt gestopt en er lucht over wordt geblazen?
Waarom zal een gerecht van water bevriezen als er in panalcohol wordt gestopt en er lucht over wordt geblazen?  Gebruik het periodiek systeem om het aantal protonen in een atoombarium te bepalen?
Gebruik het periodiek systeem om het aantal protonen in een atoombarium te bepalen?  De korrels van zand in zandsteen zijn aan hoeveel mm diameter?
De korrels van zand in zandsteen zijn aan hoeveel mm diameter?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

