
Wetenschap
Hoe snel moet een projectiel horizontaal bewegen, zodat de curve het volgt op wedstrijden van de aarde?
Inzicht in het probleem
Het projectiel moet constant naar de aarde vallen met dezelfde snelheid die het aardoppervlak ervan wegloopt. Dit creëert een cirkelvormige baan.
De sleutelvergelijking
De centripetale versnelling die nodig is om een object in een cirkelvormige baan te houden, is:
* a =v²/r
waar:
* a is de centripetale versnelling
* v is de orbitale snelheid (wat we proberen te vinden)
* r is de straal van de baan (de straal van de aarde plus de hoogte van het projectiel)
Gravitationele versnelling
De zwaartekracht van de aarde zorgt voor de centripetale versnelling. Op het aardoppervlak is de versnelling als gevolg van de zwaartekracht ongeveer:
* g =9,8 m/s²
het samenstellen
1. Stel de centripetale versnelling in gelijk aan de zwaartekrachtversnelling:
* v²/r =g
2. Los op voor V (de orbitale snelheid):
* v =√ (gr)
Voorbeeld
Laten we zeggen dat het projectiel rond een hoogte van 100 km boven het aardoppervlak is.
* r =de straal van de aarde + hoogte =6,371 km + 100 km =6,471 km =6.471.000 m
* v =√ (gr) =√ (9,8 m/s² * 6,471.000 m) ≈ 7.909 m/s
belangrijke opmerkingen
* Luchtweerstand: Deze berekening negeert de luchtweerstand, wat de snelheid en het traject van het projectiel op lagere hoogten aanzienlijk zou beïnvloeden.
* Circulaire baan: Deze berekening veronderstelt een perfect cirkelvormige baan. In werkelijkheid zijn banen vaak elliptisch.
* ontsnappingssnelheid: Als de snelheid van het projectiel groter is dan een bepaalde waarde (ontsnappingssnelheid), zal het helemaal ontsnappen aan de zwaartekracht van de aarde.
Laat het me weten als je een van deze concepten verder wilt verkennen!
 Welke metalen bezoedelen het minst?
Welke metalen bezoedelen het minst?  Welk type verbinding is negatief samengesteld of positief opgeladen?
Welk type verbinding is negatief samengesteld of positief opgeladen?  Ultrawitte coating gemodelleerd naar keverschubben
Ultrawitte coating gemodelleerd naar keverschubben Nieuw materiaal levert zacht, elastische voorwerpen die aanvoelen als menselijk weefsel
Nieuw materiaal levert zacht, elastische voorwerpen die aanvoelen als menselijk weefsel Waarom verandert de kleur van kopersulfaatoplossing in lichtgroen wanneer ijzersteden worden toegevoegd?
Waarom verandert de kleur van kopersulfaatoplossing in lichtgroen wanneer ijzersteden worden toegevoegd?
 Gemeenschappen waarschuwen voor hyperlokale stedelijke overstromingen
Gemeenschappen waarschuwen voor hyperlokale stedelijke overstromingen  Nieuwe analyse onthult wereldwijde verspreiding van giftige vervuiling en klimaatverandering
Nieuwe analyse onthult wereldwijde verspreiding van giftige vervuiling en klimaatverandering Combinatie van El Nino en de aardbeving in Ecuador in 2016 heeft de uitbraak van Zika waarschijnlijk verergerd
Combinatie van El Nino en de aardbeving in Ecuador in 2016 heeft de uitbraak van Zika waarschijnlijk verergerd Streven naar goud - de reproduceerbaarheid in hydrologische studies verbeteren
Streven naar goud - de reproduceerbaarheid in hydrologische studies verbeteren Een bron van warm water wordt een genoemd?
Een bron van warm water wordt een genoemd?
Hoofdlijnen
- Onverwachte bevinding in de energiecentrale van cellen
- Welke celorganel is verantwoordelijk voor intracellulaire digestie?
- Waar krijg je bacteriën?
- Het ontwikkelen van een symbiotische relatie tussen E. coli en stinkwantsen onthult aanwijzingen over hoe symbiose zich ontwikkelt
- Waarom zijn zoveel levende dingen afhankelijk van plantachtige protist?
- Wat zijn preformulatiestudies?
- Semantisch gesproken:verenigt betekenisstructuur talen?
- Waarom is fotosynthese nodig voor plantengroei?
- Wat is chemosynthese en hoe verschilt dit van fotosynthese?
- Nieuwe methode voor het gebruik van spingolven in magnetische materialen
- De explosie in Beiroet was een van de grootste niet-nucleaire explosies in de geschiedenis, nieuwe analyse toont

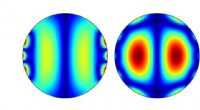
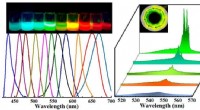
- Onderzoekers realiseren twee-foton-gepompte nanolaser van formamidiniumperovskieten
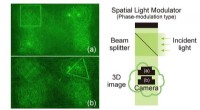
- Razendsnelle algoritmen kunnen de belasting van het genereren van 3D-hologrammen verlichten
- Wetenschapper overbrugt de kloof tussen kwantumsimulators en kwantumcomputers

 Hoe de veranderende katoensector in India tot ellende heeft geleid, ziekten, mislukking
Hoe de veranderende katoensector in India tot ellende heeft geleid, ziekten, mislukking Wanneer waargenomen bij een zuidelijke middelste breedtegraad lijken sterren?
Wanneer waargenomen bij een zuidelijke middelste breedtegraad lijken sterren?  Opschudding terwijl Oeganda een plan nastreeft om waterval in nationaal park af te dammen
Opschudding terwijl Oeganda een plan nastreeft om waterval in nationaal park af te dammen Syntheseproces om nanodeeltjes in te kapselen die antimicrobiële coatings zouden kunnen verbeteren
Syntheseproces om nanodeeltjes in te kapselen die antimicrobiële coatings zouden kunnen verbeteren Veertien jaar na de olieramp in de Golf van Mexico gaan de endemische vissen een onzekere toekomst tegemoet
Veertien jaar na de olieramp in de Golf van Mexico gaan de endemische vissen een onzekere toekomst tegemoet  Wat zijn 3 manieren waarop warmte wordt overgedragen door de atmosfeer?
Wat zijn 3 manieren waarop warmte wordt overgedragen door de atmosfeer?  Sony verbetert de prognose voor het hele jaar, registreert stevige kwartaalwinst
Sony verbetert de prognose voor het hele jaar, registreert stevige kwartaalwinst Wat is een beroemde vulkaan in Chili?
Wat is een beroemde vulkaan in Chili?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

