
Wetenschap
Hoe heeft het elastische botsing totale momentum en kinetik -energie in het systeem effect gehad?
Elastische botsingen
Een elastische botsing is een botsing waarbij kinetische energie wordt behouden. In eenvoudiger termen is de totale kinetische energie van de objecten vóór de botsing hetzelfde als de totale kinetische energie na de botsing. Er gaat geen energie verloren door warmte, geluid of vervorming. Denk aan een perfect veerkrachtige bal die botst met een hard oppervlak - de meeste energie van de bal wordt teruggegeven.
Momentum in elastische botsingen
* behoud van momentum: Momentum is altijd geconserveerd in alle botsingen, inclusief elastische. Dit betekent het totale momentum van het systeem voordat de botsing gelijk is aan het totale momentum na de botsing.
* Momentum -vergelijking: Het momentum van een object is zijn massa (m) keer zijn snelheid (v):p =mv.
* Totaal momentum: In een systeem met meerdere objecten is het totale momentum de vectorsom van de individuele momenta.
Kinetische energie in elastische botsingen
* Behoud van kinetische energie: Dit is het bepalende kenmerk van een elastische botsing. De totale kinetische energie van het systeem blijft constant.
* Kinetische energievergelijking: De kinetische energie van een object is de helft van zijn massale maal het kwadraat van zijn snelheid:KE =1/2 * MV^2.
hoe het werkt
1. Voor de botsing: De objecten hebben hun individuele momenta en kinetische energieën.
2. Tijdens de botsing: De objecten interageren, brengen momentum en kinetische energie tussen hen over.
3. Na de botsing: De objecten bewegen met nieuwe snelheden. Vanwege de natuurwetten:
* Momentum: De som van de laatste momenta van de objecten zal gelijk zijn aan de som van de initiële momenta.
* Kinetische energie: De som van de uiteindelijke kinetische energieën van de objecten zal gelijk zijn aan de som van de initiële kinetische energieën.
Voorbeeld
Stel je een biljartbal voor (a) die op 5 m/s bewegen, buigt frontaal met een stationaire biljartbal (b). Stel dat dit een perfect elastische botsing is.
* Voor de botsing:
* BALL A:Momentum =MV =(massa van a) * 5 m/s
* BALL B:Momentum =0 (stationair)
* Totaal momentum =(massa van a) * 5 m/s
* Totale kinetische energie =1/2 * (massa van a) * (5 m/s)^2
* Na de botsing:
* BALL A:Momentum =MV (nieuwe snelheid onbekend)
* BALL B:Momentum =MV (nieuwe snelheid onbekend)
* Totaal momentum =(massa van a) * (nieuwe snelheid van a) + (massa van b) * (nieuwe snelheid van b)
* Totale kinetische energie =1/2 * (massa van a) * (nieuwe snelheid van a)^2 + 1/2 * (massa van b) * (nieuwe snelheid van b)^2
Vanwege het behoud van momentum en kinetische energie kunnen de uiteindelijke snelheden van de ballen worden berekend. In dit scenario komt Ball A tot stilstand en zal Ball B met 5 m/s afgaan.
Implicaties in de praktijk
Hoewel perfect elastische botsingen zeldzaam zijn in de echte wereld, zijn de principes van toepassing op vele situaties. Inzicht in deze concepten helpt ons te analyseren:
* Botsingen in de natuurkunde: Van deeltjesfysica tot de beweging van planeten.
* Everyday Events: Het gedrag van ballen stuitert, auto's botsen (tot op zekere hoogte), en zelfs hoe moleculen op elkaar inwerken.
Laat het me weten als je nog meer vragen hebt!
 Hoeveel water stroomt er naar landbouwirrigatie?
Hoeveel water stroomt er naar landbouwirrigatie? Onderzoekers onderzoeken hoe burgers agenten kunnen worden van veranderingen in het milieu
Onderzoekers onderzoeken hoe burgers agenten kunnen worden van veranderingen in het milieu  100 miljoen jaar oude fossielen en zwaartekrachtsgolfwetenschap gebruiken om het toekomstige klimaat op aarde te voorspellen
100 miljoen jaar oude fossielen en zwaartekrachtsgolfwetenschap gebruiken om het toekomstige klimaat op aarde te voorspellen 315 atoombommen en aanhoudend lijden:de beschamende geschiedenis van kernproeven in Australië en de Stille Oceaan
315 atoombommen en aanhoudend lijden:de beschamende geschiedenis van kernproeven in Australië en de Stille Oceaan Waarom goede mensen slechte dingen doen:anticiperen op verleiding kan ethisch gedrag verbeteren, zo blijkt uit onderzoek
Waarom goede mensen slechte dingen doen:anticiperen op verleiding kan ethisch gedrag verbeteren, zo blijkt uit onderzoek
Hoofdlijnen
- Wat is een organisme dat de hele of een andere roept doodt en eet?
- Hoe cheeta's elkaar vinden na hun scheiding
- Onderzoek toont aan hoe de vogelgriep kan worden uitgeroeid door de genen van kippen te bewerken
- Wat is een organisme dat afhankelijk is van een ander voor voedsel?
- Is de beste definitie van een hypothese?
- De met uitsterven bedreigde condor verraste onderzoekers door vaderloze kuikens voort te brengen:zou 'maagdelijke geboorte' de soort kunnen redden?
- Longhornteek voor het eerst ontdekt in het noorden van Missouri
- Wat is microscoopparfocalisatie?
- Hoe dieren hun juiste grootte bereiken
- Primaire kleuren zijn rood,

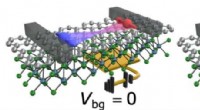
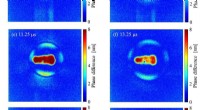
- Onderzoekers realiseren een spin-veldeffecttransistor bij kamertemperatuur
- Onderzoekers verklaren de unieke eigenschappen van slijm van hagfish

- Golven maken:een contactloze manier om schade in transparante materialen op te sporen
- Lichtversterking versnelt chemische reacties in aerosolen

 Wat zijn fenotype en genotype Welke termen die ze beschrijven?
Wat zijn fenotype en genotype Welke termen die ze beschrijven?  De negentig graadhoek van zonnestralen slaat de tropische kanker op welke datum?
De negentig graadhoek van zonnestralen slaat de tropische kanker op welke datum?  Zijn suikerkristallen een mengoplossingsverbinding of een element?
Zijn suikerkristallen een mengoplossingsverbinding of een element?  Wat is de term die wordt gebruikt om een groep weefsels te beschrijven die allemaal dezelfde functie uitvoeren?
Wat is de term die wordt gebruikt om een groep weefsels te beschrijven die allemaal dezelfde functie uitvoeren?  Wanneer worden sterren gezien?
Wanneer worden sterren gezien?  Apple probeert een hap uit de creditcardindustrie te halen
Apple probeert een hap uit de creditcardindustrie te halen Waar is koperen carbonaat van gemaakt?
Waar is koperen carbonaat van gemaakt?  Wat veroorzaakte de grootste vulkaanuitbarsting waarvan de mensheid getuige was?
Wat veroorzaakte de grootste vulkaanuitbarsting waarvan de mensheid getuige was?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

