
Wetenschap
Wat wordt bedoeld met fundamentele fysieke hoeveelheden?
Hier is een uitsplitsing:
Kenmerken:
* onafhankelijk: Ze zijn niet afgeleid van andere hoeveelheden.
* Basis voor afgeleide hoeveelheden: Alle andere fysieke hoeveelheden kunnen worden gedefinieerd met behulp van combinaties van fundamentele hoeveelheden.
* universeel: Hun definities en waarden zijn hetzelfde, ongeacht het meetsysteem.
Voorbeelden van fundamentele fysieke hoeveelheden:
* lengte: Vertegenwoordigt de afstand tussen twee punten. Gemeten in eenheden zoals meters (m), centimeters (cm), enz.
* massa: Vertegenwoordigt de hoeveelheid materie in een object. Gemeten in eenheden zoals kilogrammen (kg), gram (g), enz.
* tijd: Vertegenwoordigt de duur van de gebeurtenissen. Gemeten in eenheden zoals seconden (s), minuten (min), enz.
* Temperatuur: Vertegenwoordigt de mate van warmte of kou van een systeem. Gemeten in eenheden zoals Celsius (° C), Fahrenheit (° F), Kelvin (K), enz.
* elektrische stroom: Vertegenwoordigt de stroom van elektrische lading. Gemeten in eenheden zoals ampère (a).
* hoeveelheid substantie: Vertegenwoordigt het aantal entiteiten (atomen, moleculen, enz.) In een stof. Gemeten in eenheden zoals mol (mol).
* Lumineuze intensiteit: Vertegenwoordigt de kracht die wordt uitgestoten door een lichtbron in een bepaalde richting. Gemeten in eenheden zoals Candela (CD).
afgeleide hoeveelheden:
Afgeleide hoeveelheden worden gedefinieerd met behulp van combinaties van fundamentele hoeveelheden. Voorbeelden zijn:
* snelheid: Afstand afgelegd per tijdseenheid (lengte/tijd)
* Force: Massa -versnelling (massa * lengte/tijd²)
* Dichtheid: Massa per volume -eenheid (massa/lengte³)
* energie: Krachttijden afstand (massa * lengte²/time²)
Betekenis van fundamentele hoeveelheden:
Het begrijpen van fundamentele hoeveelheden is cruciaal voor:
* Consistentie in metingen: Het gebruik van een gedefinieerde reeks fundamentele hoeveelheden zorgt voor uniformiteit in metingen in verschillende wetenschappelijke disciplines.
* Een coherent systeem van eenheden bouwen: Fundamentele hoeveelheden vormen de basis voor het definiëren van afgeleide eenheden, waardoor een samenhangend systeem ontstaat voor het meten van fysische eigenschappen.
* Vereenvoudigde complexe fenomenen: Door complexe fysieke fenomenen uit te drukken in termen van fundamentele hoeveelheden, kunnen we deze beter begrijpen en modelleren.
Samenvattend, fundamentele fysieke hoeveelheden zijn de bouwstenen van de fysica, die dienen als basis voor het definiëren en meten van alle andere hoeveelheden. Hun onafhankelijkheid en universaliteit maken hen essentieel voor een uitgebreid begrip van de fysieke wereld.
Hoofdlijnen
- Hoe helpt marihuana de gezondheid van mensen
- Wat doet de nucleolus in een celorganel?
- Zijn organismen in dezelfde familie minder nauw verwant dan volgorde.
- Vertragen:wordt veroudering veroorzaakt door een verminderd cellulair metabolisme?
- Zalmkwekerijen verkeren in een crisis – dit is hoe wetenschappers ze proberen te redden
- Welk type organismen overleven het meest waarschijnlijk degenen met een smalle ecologische niche of brede niche?
- Sterven mensen in politiehechtenis aan opgewonden delirium?
- Waar komt ureum voornamelijk geconcentreerd?
- Reproduceren virussen prokaryotische en Eurkaryotische cellen zich door mitose?
- Stabiele topologie zien met instabiliteiten
- Onderzoek onthult een uniek moment:wanneer een luchtbel losbarst

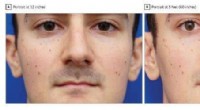
- Vervormende effecten van korte afstandsfoto's op het uiterlijk van de neus:het selfie-effect
- Onderzoekers onderzoeken nieuw mengselmateriaal dat wordt gebruikt voor kwartgolfplaatlaserstraalsplitser

- Nobelprijs voor natuurkunde wordt uitgereikt

 Technologieën schijnen de schijnwerpers op de klimaatrol van onderzeese canyons
Technologieën schijnen de schijnwerpers op de klimaatrol van onderzeese canyons Waar is de Engelse zomer gebleven?
Waar is de Engelse zomer gebleven?  Hoe lang is de Alhambra in Granada Spanje?
Hoe lang is de Alhambra in Granada Spanje?  VTT creëert een efficiënte methode voor het produceren van metalen nanodeeltjes
VTT creëert een efficiënte methode voor het produceren van metalen nanodeeltjes Krijt is een voorbeeld van wat voor soort rots?
Krijt is een voorbeeld van wat voor soort rots?  Een cricket laten stilstaan
Een cricket laten stilstaan Welke laag aarde bevat zowel de korst als de bovenste mantel?
Welke laag aarde bevat zowel de korst als de bovenste mantel?  Mechanische kracht regelt de snelheid van eiwitsynthese
Mechanische kracht regelt de snelheid van eiwitsynthese
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


