
Wetenschap
Wat is het moment van traagheid een solide halfrond?
1. Rotatieas die door het midden van het halfrond gaat en loodrecht op de basis:
In dit geval is het traagheidsmoment (i):
i =(2/5) mr²
waar:
* M is de massa van het halfrond
* R is de straal van het halfrond
2. Rotatieas die door het midden van de basis van het halfrond gaat:
In dit geval is het traagheidsmoment (i):
i =(83/320) mr²
afleiding:
Deze formules worden afgeleid met behulp van integratie en de definitie van traagheidsmoment:
i =∫ r² dm
waar:
* r is de afstand van een klein massa -element (DM) van de rotatieas
De afleiding omvat het delen van de hemisfeer in oneindig kleine massa -elementen en het integreren van hun bijdragen aan het totale traagheidsmoment.
Opmerking:
Het traagheidsmoment van een solide halfrond is altijd groter dan het traagheidsmoment van een vaste bol met dezelfde massa en straal. Dit komt omdat de massa verder wordt verdeeld over de rotatieas op het halfrond.
 Hoe heeft de wetenschap de verlichting beïnvloed?
Hoe heeft de wetenschap de verlichting beïnvloed?  NASA inventariseert fytoplanktonpopulaties in de Stille Oceaan
NASA inventariseert fytoplanktonpopulaties in de Stille Oceaan Stijgend methaan kan inspanningen om catastrofale klimaatverandering te voorkomen dwarsbomen
Stijgend methaan kan inspanningen om catastrofale klimaatverandering te voorkomen dwarsbomen Voedselwebben in bruinwatermeren zijn beter bestand tegen stikstofdepositie
Voedselwebben in bruinwatermeren zijn beter bestand tegen stikstofdepositie Welke dieren in het regenwoud zijn aaseters?
Welke dieren in het regenwoud zijn aaseters?
Hoofdlijnen
- Herbruikbare boodschappentassen moedigen het winkelend publiek aan om groenten en fruit te kopen – en junkfood?
- Welk vrouwelijk orgel is een kleine peervormige die tijdens de zwangerschap uitbreidt?
- Studie lost op waarom drinken je hongerig maakt
- Organismen in de koninkrijken eubacteria en archaebacteriën waren eerder gegroepeerd op een koninkrijk genaamd?
- Hoe diversifiëren en fylogenetisch correleren functionele kenmerken voor gelijktijdig voorkomende ondersoorten in boreale bossen?
- Wat zijn mitochondria niet gevonden?
- Welke vier conditie moeten bacteriën hebben om te fokken?
- Hoe bacteriën zo snel reageren op externe veranderingen
- Waarom hebben we hondsdolheid nog niet uitgeroeid?
- De elektronenspin regelen:draai het snel maar voorzichtig om

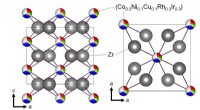
- Overgangsmetaalcocktail helpt bij het maken van gloednieuwe supergeleiders
- Wetenschappers kraken de paranotenpuzzel, hoe komen de grootste noten naar boven?

- Nieuw kwantumapparaat ingesteld om meetstandaarden van elektrische stroom te ondersteunen

- Partitiefunctie-nullen zijn een snelkoppeling naar thermodynamische berekeningen op kwantumcomputers

 Tool voor niet-statistici genereert automatisch modellen die inzichten halen uit complexe datasets
Tool voor niet-statistici genereert automatisch modellen die inzichten halen uit complexe datasets Wat was het ruimtevaartuig dat werd gebruikt in Apollo 1?
Wat was het ruimtevaartuig dat werd gebruikt in Apollo 1?  Welke eigenschappen delen het jodendom en de islam?
Welke eigenschappen delen het jodendom en de islam?  Hoe vormt grondwater?
Hoe vormt grondwater?  Welke planeten hebben geen ringen om hen heen?
Welke planeten hebben geen ringen om hen heen?  Hoe beïnvloedt water het reizen van radiofrequentie?
Hoe beïnvloedt water het reizen van radiofrequentie?  Wat is de opwaartse kracht die inwerkt op de vleugel van een vliegtuig tijdens de vlucht?
Wat is de opwaartse kracht die inwerkt op de vleugel van een vliegtuig tijdens de vlucht?  Welke vorm van energie wordt geproduceerd door Hydro?
Welke vorm van energie wordt geproduceerd door Hydro?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

