
Wetenschap
Wat is de minimale snelheid die nodig is om een lichaam van hoogte H te projecteren, zodat het niet op aarde zal vallen?
Inzicht in Escape Velocity
* Gravitationele potentiële energie: Naarmate een object verder weg van de aarde beweegt, neemt de energie van het zwaartekracht ervan toe.
* Kinetische energie: Om te ontsnappen aan de zwaartekracht van de aarde, heeft het object voldoende kinetische energie nodig om de energie -energie van zwaartekracht te overwinnen.
* balans: Bij ontsnappingssnelheid is de kinetische energie van het object gelijk aan de zwaartekrachtpotentiaal energie bij oneindig (waarbij de zwaartekracht als nul wordt beschouwd).
afleiding
1. Gravitationele potentiële energie bij oneindigheid:
- De potentiële energie bij oneindig wordt gedefinieerd als nul.
- De verandering in potentiële energie van het aardoppervlak tot oneindig wordt gegeven door:
- Δpe =gmm/r
Waar:
-G is de zwaartekrachtconstante (6.674 x 10^-11 m^3 kg^-1 s^-2)
- M is de massa van de aarde (5.972 x 10^24 kg)
- M is de massa van het object
- R is de straal van de aarde (6.371 x 10^6 m)
2. Kinetische energie bij ontsnappingssnelheid:
- ke =(1/2) mv^2
- V is de ontsnappingssnelheid
3. Kinetische en potentiële energie gelijkstellen:
- (1/2) mv^2 =gmm/r
4. Oplossing voor ontsnappingssnelheid:
- V^2 =2GM/R
- v =√ (2 g/r)
ontsnappingssnelheid van hoogte 'H'
Als het object wordt gelanceerd vanuit een hoogte 'H' boven het aardoppervlak, wordt de effectieve afstand van het midden van de aarde r + h. Daarom is de ontsnappingssnelheid van hoogte 'H':
v =√ (2gm/(r + h))
belangrijke opmerkingen
* Deze formule veronderstelt geen luchtweerstand. In werkelijkheid zal luchtweerstand de vereiste snelheid aanzienlijk beïnvloeden.
* De ontsnappingssnelheid hangt niet af van de massa van het object. Dit komt omdat de zwaartekracht en de vereiste kinetische energie beide evenredig schalen met de massa van het object.
Laat het me weten als je een numeriek voorbeeld wilt of verdere concepten wilt verkennen die verband houden met ontsnappingssnelheid!
 De temperatuurschaal die wetenschappers vaak gebruiken is de?
De temperatuurschaal die wetenschappers vaak gebruiken is de?  Waarom reinigen zuren koperen munten het beste?
Waarom reinigen zuren koperen munten het beste?  Wetenschappers ontwikkelen met maleïnezuur behandelde bacteriële cellulosegel voor het verbeteren van botherstel
Wetenschappers ontwikkelen met maleïnezuur behandelde bacteriële cellulosegel voor het verbeteren van botherstel  Ionische verbindingen zoals natriumchloride NaCl lossen gemakkelijk op in water?
Ionische verbindingen zoals natriumchloride NaCl lossen gemakkelijk op in water?  Reageert natrium en kalium gewelddadig met water een chemische of fysieke verandering?
Reageert natrium en kalium gewelddadig met water een chemische of fysieke verandering?
Hoofdlijnen
- Wat is de relatie tussen cellenweefsels en organen?
- Wat is de functie van sucrose bij DNA -extractie?
- Model suggereert hoe de code van het leven uit de oersoep voortkwam
- Wat voor soort organismen groeien er onder rotsen op Red en leven misschien zelfs op Mars?
- Wat is de klasse van hibiscusplanten?
- Welke invloed heeft big data op sportanalyses?
- Waar vinden de celreacties plaats?
- Kleine dierenharen kunnen werken als gevoelige kompasnaalden
- Wat zou het beste hulpmiddel zijn om cellen te bekijken in een wetenschappelijk onderzoek?
- Hoe hard is te hard als het gaat om sportfluitjes?

- Een lawine van geweld:analyse onthult voorspelbare patronen in gewapende conflicten

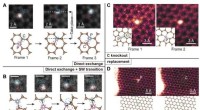
- Atomen één voor één manipuleren met een elektronenstraal
- Onderzoekers ontwikkelen een krachtige, draagbare terahertz-laser

- Supernauwkeurige sensor kan leiden tot het produceren van nog kleinere chips

 Verwarmt oceaanmaan Enceladus miljarden jaren lang
Verwarmt oceaanmaan Enceladus miljarden jaren lang Wat is de relatie van betoverd koninkrijk tot natuurkunde?
Wat is de relatie van betoverd koninkrijk tot natuurkunde?  Wat kunt u gebruiken om een vulkaanuitbarsting te maken naast bakpoeder en azijn?
Wat kunt u gebruiken om een vulkaanuitbarsting te maken naast bakpoeder en azijn?  Kan een app uw romantische relatie verbeteren?
Kan een app uw romantische relatie verbeteren?  Wat is een heuvel met vlakke top en steile zijkanten?
Wat is een heuvel met vlakke top en steile zijkanten?  Hoe helpen de gegevens van bewegingen van seismische golven geologen om het aardbevingrisico voor een gebied te bepalen?
Hoe helpen de gegevens van bewegingen van seismische golven geologen om het aardbevingrisico voor een gebied te bepalen?  Wanneer natriumchloride oplost in water en het ionenchloor wordt omringd door moleculen, zal deze oplossing elektriciteit leiden?
Wanneer natriumchloride oplost in water en het ionenchloor wordt omringd door moleculen, zal deze oplossing elektriciteit leiden?  Wat is de juiste chemische formule en naam voor samengestelde Cu2SO4?
Wat is de juiste chemische formule en naam voor samengestelde Cu2SO4?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

