
Wetenschap
Met welke minimale snelheid moet een persoon de grond verlaten om zijn massamiddelpunt 1,85 op te tillen en de bar met 0,65 te kruisen?
1. Definieer het doel:
We moeten de initiële verticale snelheid (V₀) vinden die nodig is voor een persoon om een hoogte van 1,85 meter (massamentrum) te bereiken plus 0,65 meter (dwarsbalk), in totaal 2,5 meter.
2. Stel de energievergelijking in:
* Initiële energie: De persoon begint alleen met kinetische energie (KE):
Ke =(1/2) MV₀²
* Final Energy: Op het hoogste punt heeft de persoon alleen potentiële energie (PE):
PE =MGH
Waar:
* m =massa van de persoon
* v₀ =initiële verticale snelheid
* g =versnelling als gevolg van zwaartekracht (9,8 m/s²)
* h =totale hoogte (2,5 meter)
3. Pas instandhouding van energie toe:
Omdat energie wordt geconserveerd, moet de initiële kinetische energie gelijk zijn aan de uiteindelijke potentiële energie:
(1/2) mv₀² =mgh
4. Los op voor de beginsnelheid (v₀):
* Annuleer de massa (M) aan beide kanten.
* Herschik de vergelijking om op te lossen voor v₀:
V₀² =2GH
v₀ =√ (2GH)
5. Bereken de beginsnelheid:
* Vervang de waarden:
v₀ =√ (2 * 9,8 m/s² * 2,5 m)
V₀ ≈ 7,0 m/s
Daarom moet de persoon de grond verlaten met een minimale snelheid van ongeveer 7,0 meter per seconde om de lat te wissen.
 Is de ontvlambaarheid van ethanol een chemische eigenschap of eigenschap?
Is de ontvlambaarheid van ethanol een chemische eigenschap of eigenschap?  Hoeveel waterstofatomen zijn er in 7,40 mol ammoniumsulfide?
Hoeveel waterstofatomen zijn er in 7,40 mol ammoniumsulfide?  Wat is het wetenschappelijke veiligheidssymbool voor het nooit proeven of ruiken van een onbekende stof?
Wat is het wetenschappelijke veiligheidssymbool voor het nooit proeven of ruiken van een onbekende stof?  Is een metaal oplosbaar in water?
Is een metaal oplosbaar in water?  Duidelijkere en beter gefocuste SEM-beelden
Duidelijkere en beter gefocuste SEM-beelden
 Hoe bosbranden grotere effecten op wolkenvorming kunnen hebben dan eerder werd gedacht
Hoe bosbranden grotere effecten op wolkenvorming kunnen hebben dan eerder werd gedacht Onderzoekers identificeren bacteriën en virussen die uit de oceaan zijn uitgestoten
Onderzoekers identificeren bacteriën en virussen die uit de oceaan zijn uitgestoten Waarom zien mannetjes en vrouwtjes van sommige soorten er zo verschillend uit?
Waarom zien mannetjes en vrouwtjes van sommige soorten er zo verschillend uit?  Hoe 'afluisterende' Afrikaanse herbivoren reageren op alarmoproepen
Hoe 'afluisterende' Afrikaanse herbivoren reageren op alarmoproepen  Wat maakt het uit? Waarom de evolutie suggereert dat de verantwoordelijkheid voor het ouderschap zelden gelijkelijk wordt gedeeld
Wat maakt het uit? Waarom de evolutie suggereert dat de verantwoordelijkheid voor het ouderschap zelden gelijkelijk wordt gedeeld
Hoofdlijnen
- Wat zijn de concepten over wetenschappelijke geletterdheid?
- Ondergingen dinosauriërs een langdurige achteruitgang voordat ze massaal uitstierven?
- Waarom evolueerden mensen maar wangen?
- Welke functies zorgen ervoor dat het osmotische en pH-evenwicht in het bloed behouden blijft?
- Hoe Hydra-dieren hun eigen hoofd regenereren
- Van welke cellulaire organellysosomen worden gevormd door ontluiken?
- Welke term beschrijft het beste hoe een organismen zorgt om zijn jonge winterslaapjes en een karakteristieke manier van paren heeft?
- Zwaarlijvige honden geholpen door effectieve gewichtsverliesproeven
- Giftige Death Cap-paddenstoel verspreidt zich over Noord-Amerika
- 'S Werelds kleinste vergrootglas maakt het mogelijk om chemische bindingen tussen atomen te zien

- Laserbursts sturen de snelste logische poorten ooit aan

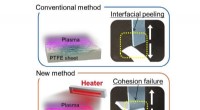
- Onderzoekers maken de gladste oppervlakken klevend
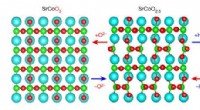
- Wetenschappers doen tot nu toe de meest gevoelige metingen van de geleidbaarheid van silicium

- Een materiaal dat kan schakelen tussen meerdere fasen met verschillende elektronische, optische en magnetische eigenschappen
 Welke materialen worden sneller warm?
Welke materialen worden sneller warm?  Wat is een broomacceptor?
Wat is een broomacceptor?  Hoe lang moet een kracht van 100 N werken op lichaam 20kg zodat het aquires snelheid MS?
Hoe lang moet een kracht van 100 N werken op lichaam 20kg zodat het aquires snelheid MS?  Welke invloed heeft de hoogteverandering vanaf waar een bal valt op het stuiteren ervan?
Welke invloed heeft de hoogteverandering vanaf waar een bal valt op het stuiteren ervan?  Telescoopprotesten in Hawaï trekken supporters om project te verdedigen
Telescoopprotesten in Hawaï trekken supporters om project te verdedigen Video:Nanosponge-lokvogel bestrijdt superbacteriën
Video:Nanosponge-lokvogel bestrijdt superbacteriën Wat is de parallelle afstemming van mineralen die benadrukt zijn?
Wat is de parallelle afstemming van mineralen die benadrukt zijn?  De elektrische kracht is veel zwakker dan de zwaartekracht?
De elektrische kracht is veel zwakker dan de zwaartekracht?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

