
Wetenschap
Een thermometer wordt uit een kamer gehaald waar de temperatuur 20C is en buiten 5C. Na één minuut staat er 12C. Wanneer wordt er 6C aangegeven?
Omdat de temperatuur daalt, kunnen we de differentiaalvergelijking schrijven:
$$\begin{uitlijnen}\frac{dT}{dt} =k(T-5) \end{uitlijnen}$$
waarbij k een positieve constante is.
Door variabelen te scheiden en te integreren, krijgen we:
$$\begin{align} \frac{1}{T-5}dT =kdt\end{align}$$
$$\ln |T-5|=kt+C_1$$
$$T-5=Ce^{kt} $$
$$T=Ce^{kt}+5 $$
Met behulp van de beginvoorwaarde \(T(0)=20\) vinden we dat \(C=15\)
Daarom is de oplossing van de differentiaalvergelijking (1).
$$T(t)=15e^{kt}+5$$
Met behulp van de andere gegeven voorwaarde \(T(1)=12\) vinden we dat
$$12=15e^k+5$$
$$e^k=\frac{7}{10} \daarom $$
$$k=\ln\frac{7}{10} $$
De oplossing van de differentiaalvergelijking (1) wordt dus:
$$\boxed{T(t)=15 e^{\left ( \ln \frac{7}{10} \right ) t} +5 }$$
Instelling \(T=6\) krijgen we uiteindelijk
$$6=15e^{(\ln \frac{7}{10})t}+5$$
$$1=15e^{(\ln \frac{7}{10})t}$$
$$\frac{1}{15}=e^{(\ln \frac{7}{10})t}$$
$$(\frac{1}{15})^{\frac{1}{\ln \frac{7}{10}}} =t $$
$$t=\frac{\ln{\frac{1}{15}}}{\ln \frac{7}{10}}$$
$$t=\frac{\ln 1-\ln15}{ \ln7-\ln 10} \circa 1,23\text{ minuten}$$
Daarom duurt het ongeveer 1,23 minuten voordat de thermometer C aangeeft.
 Bloedvlekken gebruiken op plaats delict om de leeftijd van een verdachte of slachtoffer te bepalen
Bloedvlekken gebruiken op plaats delict om de leeftijd van een verdachte of slachtoffer te bepalen Een kleine stilling bouwen
Een kleine stilling bouwen Wat is het soort verval dat resulteert in de vorming van een ander element?
Wat is het soort verval dat resulteert in de vorming van een ander element?  Een scheikundige heeft één oplossing die voor 80 procent uit zuur bestaat en nog eens uit 30 procent. Hoeveel van de eerste oplossing is nodig om 400 L 62 zuur te maken?
Een scheikundige heeft één oplossing die voor 80 procent uit zuur bestaat en nog eens uit 30 procent. Hoeveel van de eerste oplossing is nodig om 400 L 62 zuur te maken?  Waar bestaat rioolwater voornamelijk uit?
Waar bestaat rioolwater voornamelijk uit?
 NASA ontdekt dat droogte in de Amazone een lange erfenis van schade nalaat
NASA ontdekt dat droogte in de Amazone een lange erfenis van schade nalaat NASA ziet de oostelijke Stille Oceaan de tropische storm Norma opwekken
NASA ziet de oostelijke Stille Oceaan de tropische storm Norma opwekken Waarom lopen kinderen niet meer naar school?
Waarom lopen kinderen niet meer naar school?  Eenvoudige regel voorspelt wanneer een ijstijd eindigt
Eenvoudige regel voorspelt wanneer een ijstijd eindigt Beken stoten mogelijk meer koolstofdioxide uit in een warmer klimaat
Beken stoten mogelijk meer koolstofdioxide uit in een warmer klimaat
Hoofdlijnen
- Spiegelbeeldmoleculen onthullen droogtestress in bossen
- Zoekers in Mexico vinden, maar laat los, vaquita bruinvis kalf
- Wat zijn genetisch gemodificeerde organismen (GGO's)? Zijn ze veilig?
- Nieuwe mobiele app diagnosticeert gewasziekten in het veld en waarschuwt boeren op het platteland
- Zebravissen geven verrassend inzicht in hoe de hersenen reageren als de temperatuur stijgt
- Chimpansees kunnen leren gereedschap te gebruiken zonder anderen te observeren
- Hoe cellen zichzelf verdedigen tegen antibiotica en cytostatica
- Team ontwikkelt technologie voor de productie van bioplastics uit landbouw- en voedselbijproducten
- Stikstofvervuiling is minder schadelijk voor gemengde bossen, blijkt uit onderzoek
- Nieuwe aanpak levert zeer zuiver radium op voor medische toepassingen
- Wrap van nanomateriaal voor verbeterde weefselbeeldvorming

- De handigheid van licht is de sleutel tot betere optische controle
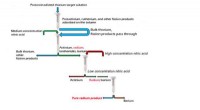
- Onderzoekers demonstreren niet-destructieve midden-infraroodbeeldvorming met behulp van verstrengelde fotonen

- LHCb onthult het geheim van het ontstaan van antimaterie in kosmische botsingen

 Volkswagen en Mercedes ondertekenen akkoord over EV-batterij met Canada
Volkswagen en Mercedes ondertekenen akkoord over EV-batterij met Canada Nieuwe computationele methodologie geeft onverwachte antwoorden op twee Hilbert-problemen
Nieuwe computationele methodologie geeft onverwachte antwoorden op twee Hilbert-problemen Wat zijn de vier eukaryotische koninkrijken?
Wat zijn de vier eukaryotische koninkrijken?  Wat is jouw massa op elke planeet?
Wat is jouw massa op elke planeet?  Waarom knalt en brandt hout?
Waarom knalt en brandt hout?  Recyclage van koolstofdioxide? 'Diagonale' benadering voor reducerende functionaliteit van koolstof
Recyclage van koolstofdioxide? 'Diagonale' benadering voor reducerende functionaliteit van koolstof  Wetenschappers verbeteren diagnose alvleesklierkanker met multifunctionele platina-nanoreactor
Wetenschappers verbeteren diagnose alvleesklierkanker met multifunctionele platina-nanoreactor Hoe zal klimaatverandering de watervoorraden beïnvloeden?
Hoe zal klimaatverandering de watervoorraden beïnvloeden?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

