
Wetenschap
Hoe kun je bewijzen dat het beeld gevormd in een vlakke spiegel zich even ver achter het object ervoor bevindt?
Beschouw een object AB dat loodrecht op een vlakke spiegel XX' is geplaatst op een afstand d ervan. Laat A'B' het beeld zijn van AB gevormd door de spiegel.
Teken een lichtstraal vanuit punt A evenwijdig aan de spiegel. Het zal de spiegel raken op punt C en evenwijdig aan zichzelf worden teruggekaatst, waarbij het punt B' raakt.
Trek nog een lichtstraal vanuit punt B evenwijdig aan de spiegel. Het zal de spiegel raken in punt D en evenwijdig aan zichzelf worden teruggekaatst, waarbij het punt A' raakt.
De twee gereflecteerde stralen kruisen elkaar in punt I, wat de schijnbare locatie is van het beeld van punt AB.
Laat AO en BI loodrecht staan op respectievelijk de punten A en B op de spiegel XX'. Dan kunnen we vaststellen dat:
$$\driehoek AOC \sim \driehoek BOI$$
Dit komt omdat:
1. De hoeken AOC en BOI zijn beide rechte hoeken.
2. De hoeken CAO en IBO zijn beide gelijk, aangezien de invallende straal en de gereflecteerde straal gelijke hoeken maken met het oppervlak van de spiegel.
3. De zijde AO is evenwijdig aan zijde BI, aangezien beide loodrecht staan op XX'.
Daarom hebben we, door de gelijkenis van de driehoek:
$$\frac{AO}{OI} =\frac{BO}{IB}$$
$$OI=AO, \ en \ BI=BO$$
Door beide zijden te vermenigvuldigen met OI verkrijgen we
$$OI^2 =AO\maal BO$$
Hieruit volgt dat,
$$d =u \tag 1$$
$$v =-d \tag 2$$
Als we (1) en (2) optellen, hebben we:
$$d-d=u-v$$
$$\Pijl naar rechts \mathbf{2d=u-v}$$
 Van insect tot medicijn - speeksel van teken kan de sleutel zijn tot de behandeling van hartaandoeningen
Van insect tot medicijn - speeksel van teken kan de sleutel zijn tot de behandeling van hartaandoeningen Biocompatibel binair hologram met mogelijkheden voor medicijnelutie
Biocompatibel binair hologram met mogelijkheden voor medicijnelutie Wolfraamisotoop helpt bij het bestuderen van hoe toekomstige fusiereactoren kunnen worden bepantserd
Wolfraamisotoop helpt bij het bestuderen van hoe toekomstige fusiereactoren kunnen worden bepantserd  Een fullereenachtig molecuul dat volledig uit metaalatomen bestaat
Een fullereenachtig molecuul dat volledig uit metaalatomen bestaat  Wat is de oxidatietoestand van Hg in Hg2Cl2?
Wat is de oxidatietoestand van Hg in Hg2Cl2?
 Studie analyseert de impact van koolstofdioxide op het klimaat op aarde 30 miljoen jaar geleden
Studie analyseert de impact van koolstofdioxide op het klimaat op aarde 30 miljoen jaar geleden Verschillende plaatinterfaces gevonden in de overgangszone van de mantel
Verschillende plaatinterfaces gevonden in de overgangszone van de mantel Klimaatverandering zorgt voor ineenstorting van mariene voedselwebben
Klimaatverandering zorgt voor ineenstorting van mariene voedselwebben Dodelijkste bosbrand in Californië eindelijk getemd
Dodelijkste bosbrand in Californië eindelijk getemd Waarom zijn ecosystemen zo belangrijk?
Waarom zijn ecosystemen zo belangrijk?
Hoofdlijnen
- Hoe bestrijden planten ziekten?
- Onderzoekers ontdekken het mechanisme voor bewegingen van blaasjes over korte afstanden
- Vermont ziet hedendaags record voor reproductie van Amerikaanse zeearenden
- Waar bevinden zich lipiden in het lichaam?
- Onderzoekers onderzoeken effecten van tau-eiwitten op microtubuli in zenuwcellen
- Wat zijn de twee hoofdfasen van celdeling?
- Hoe technologie ons in staat stelt de geheimen van de Amazone-biodiversiteit te onthullen
- Is het ethisch om stamcellen te gebruiken?
- Is MLB klaar om te strijden om de volgende generatie fans?
- Hoeveel weegt een kilogram?

- Niet-lineaire golfmenging maakt beeldvorming onder de golflengte mogelijk

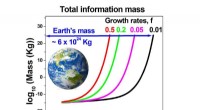
- Digitale inhoud op schema om de massa van de halve aarde te evenaren met 2245
- Tijdwaarnemingstheorie combineert kwantumklokken en Einsteins relativiteit

- Gesimuleerde berekeningen bevestigen met experimentresultaten
 Wat is de ideale gaswet?
Wat is de ideale gaswet?  Canada, als Trudeau wint, om in 2050 netto nuluitstoot te bereiken:minister
Canada, als Trudeau wint, om in 2050 netto nuluitstoot te bereiken:minister Video:Is er een snelle oplossing voor de verzuring van de oceanen?
Video:Is er een snelle oplossing voor de verzuring van de oceanen?  Wat is het sterkste zure citroensap met een pH van 2,5 of tomaat 4,5?
Wat is het sterkste zure citroensap met een pH van 2,5 of tomaat 4,5?  Hoe je het kerstdiner zo milieuvriendelijk mogelijk kookt
Hoe je het kerstdiner zo milieuvriendelijk mogelijk kookt  5 Verbijsterende subatomaire deeltjes
5 Verbijsterende subatomaire deeltjes  Een betere manier om fosfor te beheren?
Een betere manier om fosfor te beheren?  Bijna 200 melden dat vuurballen over de noordoostelijke hemel schieten
Bijna 200 melden dat vuurballen over de noordoostelijke hemel schieten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

