
Wetenschap
Doorbraak in lichtmanipulatie:onthulling van nieuwe eindige barrière-gebonden toestanden
Het onderzoeken van golfvoortplanting en lokalisatie in verschillende media is een kernfocus in de optica en akoestiek. In het bijzonder op het gebied van de fotonica en de fonetiek hebben wetenschappers zich toegelegd op het begrijpen en controleren van het gedrag van licht- en geluidsgolven in periodieke media.
Met hun unieke bandgap-eigenschappen bieden fotonische kristallen een uitstekend platform voor het bestuderen van golfvoortplanting en lokalisatie. Deze bandafstanden, veroorzaakt door de periodieke structuur van het kristal, kunnen de voortplanting van golven controleren en zelfs golven in bepaalde frequentiebereiken volledig remmen.
Traditioneel werd aangenomen dat grensmodi in fotonische kristallen sterk worden beïnvloed door de grootte van het kristal (aantal roosterlocaties). Algemeen werd aangenomen dat deze modi gemakkelijker beperkt kunnen worden in grote systemen (met veel roosterlocaties), aangezien de kans op tunneling aanzienlijk afneemt naarmate de systeemomvang groter wordt. Dit fenomeen is van cruciaal belang bij het ontwerpen en implementeren van hoogwaardige fotonische apparaten, vooral bij het nastreven van hoge integratie en miniaturisatie van apparaten.
Bovendien hebben gebonden toestanden in het continuüm (BIC's) in het onderzoek naar fotonische kristallen de aandacht getrokken, omdat ze onthullen dat bepaalde unieke modi zelfs binnen het continue spectrum binnen specifieke regio's kunnen worden beperkt. Dit fenomeen biedt een nieuw perspectief voor het begrijpen en beheersen van de lokalisatie van lichtgolven. Het toont een groot potentieel in praktische toepassingen, zoals het verbeteren van de prestaties en efficiëntie van optische apparaten.
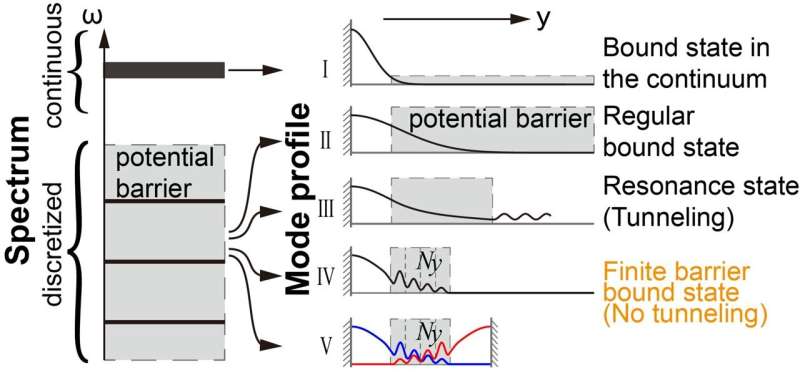
Nieuw onderzoek gepubliceerd in Light:Science &Applications stelt en bevestigt het bestaan van eindige barrière-gebonden staten. Het spectrum van een systeem bestaat doorgaans uit continue en discrete spectra (linkerpaneel van figuur 1). Conventionele wijsheid stelt dat het eigenwaardespectrum van gebonden toestanden discreet is, terwijl ongebonden toestanden een continu spectrum vormen.
Als in elektronische systemen bijvoorbeeld de energie van het deeltje lager is dan de potentiële energie op oneindig, is de toestand gebonden aan een discreet spectrum; terwijl deeltjes met een energie hoger dan de potentiële energie zich verspreiden en een continu spectrum vormen.
Voor licht- en geluidsgolven ontstaan discrete toestanden als gevolg van randvoorwaarden die door een barrière worden opgelegd, zoals een 'bandgap'. Deze discrete toestanden kunnen volledig worden gelokaliseerd in ideale omstandigheden (oneindige barrièrebreedte, figuur 1-II). Wanneer de breedte van de barrière echter eindig is, bestaat de kans dat de toestand door de barrière heen tunnelt en een resonante toestand wordt (Fig. 1-III).
Met name zijn gebonden toestanden in het continuüm (BIC's) ruimtelijk gebonden binnen het energie-/frequentiebereik van het continue spectrum (Fig. 1-I). Deze studie introduceert een contra-intuïtief concept parallel aan BIC's:bepaalde toestanden kunnen volledig gebonden zijn in zeer dunne bandgap-materialen, waardoor ze niet door het bandgap-materiaal kunnen tunnelen (Fig. 1-IV en 1-V).
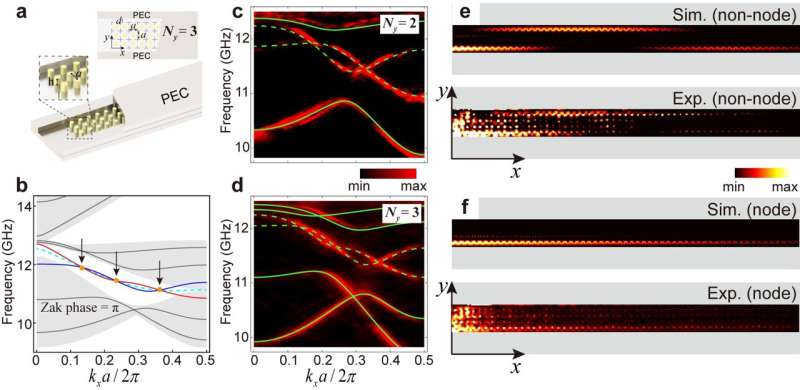
De studie demonstreert eerst een speciale spiegelsymmetrische fotonische kristalstrookstructuur waarmee de overgang van grensmodi nauwkeurig kan worden gecontroleerd. Wanneer de breedte van het fotonische kristal (het aantal roosterlocaties langs de y-richting, Ny ) klein is, werken de grensmodi aan beide kanten samen en worden ze opgesplitst in oneven en even modi (Fig. 2 a – d).
Bij specifieke golfvectoren (knopen) is de koppelsterkte van de grensmodi nul. Zelfs als de breedte (Ny ) van het fotonische kristal erg klein is, kan de grensmodus niet van de ene kant van het fotonische kristal naar de andere springen (Fig. 2 e – f). Over het algemeen wordt aangenomen dat er veel roosterlocaties nodig zijn om de koppeling van grensmodi te onderdrukken. Toch daagt deze studie deze visie uit en opent een nieuwe methode voor het manipuleren van fotongedrag op microscopische schaal.
Na de vorige configuratie verwijderen onderzoekers één PEC-grens van het fotonische kristal, waardoor een nieuwe configuratie zichtbaar wordt. Ze ontdekten dat de resterende grensmodi bij specifieke knooppuntgolfvectoren volledig gevangen zitten, waardoor Finite Barrier Enabled Bound States in the Continuum (FBIC's) worden gevormd.
Deze FBIC's vertonen niet-stralende eigenschappen vanwege de ontkoppeling van de twee grensmodi. Op de knooppunten, waar de koppelsterkte van grensmodi nul is, bestaat er een toestand met een stralingscoëfficiënt van nul wanneer één zijde van de PEC wordt verwijderd, en de frequentie ervan overeenkomt met de knooppuntfrequentie gevonden in het dubbele PEC-scenario, waardoor het wordt geïdentificeerd als een FBIC.
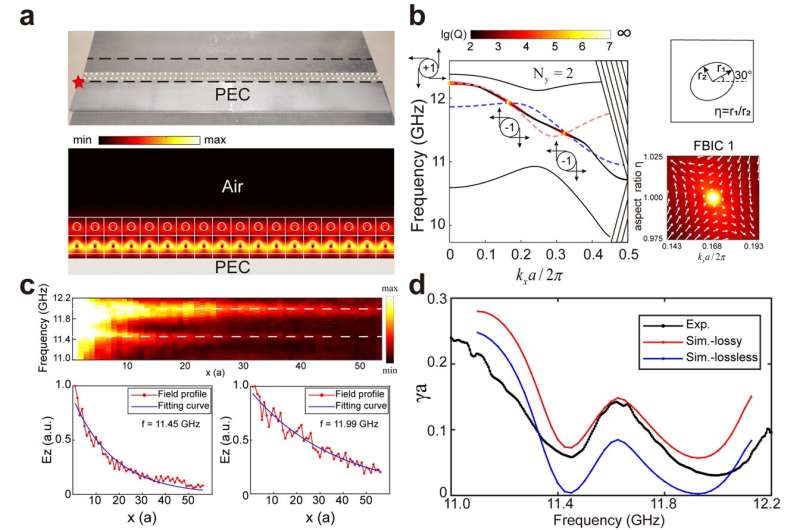
Door het circulaire diëlektricum te veranderen in elliptisch om de oorspronkelijke spiegelsymmetrie te doorbreken en een nieuwe geometrische parameter η te introduceren, definieerde de studie bovendien een wikkelingsgetal in de kx-η parameterruimte, waardoor de topologische kenmerken van FBIC's werden onthuld en deze modi als BIC's werden bevestigd ( Afb. 3 a–b).
Rekening houdend met het onvermijdelijke diëlektrische verlies bij microgolffrequenties, heeft de studie FBIC's experimenteel gevalideerd door de verzwakking van grensmodi te meten (Fig. 3 c – d), wat de volledige lokalisatie van grensmodi binnen zeer weinig roosterlocaties (Ny aantoont).> =2, 3, enz.), wat een nieuwe aanpak biedt om BIC's te bereiken.
Deze baanbrekende studie onderzoekt nieuwe fysische verschijnselen in fotonische kristallen en bereikt een nauwkeurige controle van grensmodi. Dit werk biedt niet alleen theoretisch een nieuw inzicht in het tunnelen en begrenzen van grensmodi in fotonische kristallen, maar bevestigt ook de volledige lokalisatie van grensmodi bij specifieke golfvectoren door middel van microgolfexperimenten, waardoor een nieuw perspectief op het gebied van de fotonica ontstaat.
Het onderzoek onthult nieuwe methoden voor het manipuleren van fotongedrag, wat belangrijk is voor de ontwikkeling van sterk geïntegreerde fotonische apparaten. Het biedt ook nieuwe strategieën voor het gebruik van fotonische kristallen om de interacties tussen licht en materie te verbeteren, wat mogelijk kan leiden tot doorbraken in niet-lineaire optica en interacties tussen licht en tweedimensionale materialen. Deze bevindingen kunnen toekomstig onderzoek inspireren, zoals het toepassen van deze principes op andere golfsystemen zoals fononische kristallen.