Wetenschap
Nieuw model biedt op fysica geïnspireerde beoordeling van ranglijsten
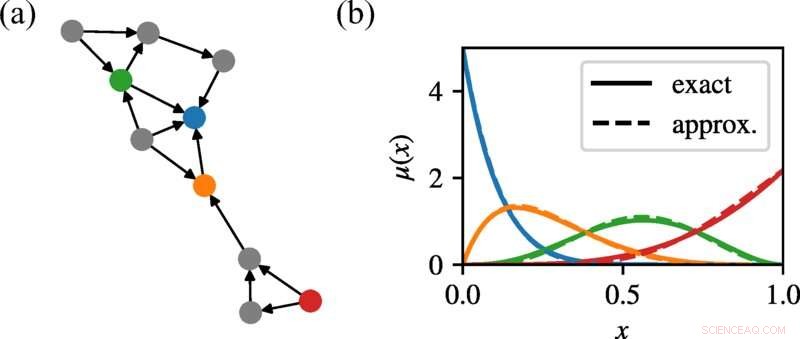
In (a) tonen we een willekeurig gegroeid netwerk met Poisson out-degree. In (b) tonen we de achterste marginalen voor vier representatieve knooppunten, gekleurd om overeen te komen met (a), waarbij we die verkregen door onze methode vergelijken met de exacte resultaten van uitputtende opsomming. Ondanks de aanwezigheid van korte cycli, benadert onze geloofsvoortplantingsbenadering de marginalen vrij goed, en komt niet alleen overeen met de middelen, maar ook met de vormen van deze distributies. Krediet:Fysieke beoordeling E (2022). DOI:10.1103/PhysRevE.105.L052303
De wereld staat vol met ranglijsten en bestellingen. Ze verschijnen in tennis - zoals in de Franse Open, die eindigt met een definitieve ranglijst van kampioensspelers. Ze komen voor bij pandemieën, zoals wanneer volksgezondheidsfunctionarissen nieuwe infecties kunnen registreren en contacttracering kunnen gebruiken om netwerken van verspreiding van COVID-19 te schetsen. Systemen van competitie, conflict en besmetting kunnen allemaal aanleiding geven tot hiërarchieën.
Deze hiërarchieën worden echter achteraf waargenomen. Dat maakt het moeilijk om de echte ranglijst van het systeem te kennen:wie was eigenlijk de beste speler? Wie heeft wie besmet? "Je kunt niet terug in de tijd gaan en precies leren hoe dit is gebeurd", zegt SFI Postdoctoral Fellow George Cantwell. Je zou een model van het netwerk kunnen bouwen en alle mogelijke uitkomsten kunnen vergelijken, maar zo'n brute-force-aanpak wordt al snel onhoudbaar. Als je bijvoorbeeld een groep probeert te rangschikken met slechts 60 deelnemers, bereikt het aantal mogelijke permutaties het aantal deeltjes in het bekende universum.
Voor een recent artikel gepubliceerd in Physical Review E , werkte Cantwell samen met SFI-professor Cris Moore, een computerwetenschapper en wiskundige, om een nieuwe manier te beschrijven om ranglijsten te evalueren. Hun doel was niet om één echte hiërarchie te vinden, maar om de spreiding van alle mogelijke hiërarchieën te berekenen, waarbij elke hiërarchie werd gewogen op basis van zijn waarschijnlijkheid.
"We waren bereid om niet precies gelijk te hebben, maar we wilden goede antwoorden krijgen met enig gevoel over hoe goed ze zijn", zegt Cantwell. Het nieuwe algoritme is geïnspireerd op de natuurkunde:rangen worden gemodelleerd als interagerende entiteiten die omhoog of omlaag kunnen bewegen. Door die lens gedraagt het systeem zich dan als een fysiek systeem dat kan worden geanalyseerd met methoden uit de spinglastheorie.
Kort na het begin van de COVID-19-pandemie begonnen Cantwell en Moore na te denken over modellen van hoe ziekte zich via een netwerk verspreidt. Ze herkenden de situatie snel als een ordeningsprobleem dat zich in de loop van de tijd voordoet, vergelijkbaar met de verspreiding van een meme op sociale media of de opkomst van kampioenschapsranglijsten in professionele sporten. "Hoe bestel je dingen als je onvolledige informatie hebt?" vraagt Cantwell.
Ze begonnen met het bedenken van een functie die een rangorde zou kunnen scoren op nauwkeurigheid. Bijvoorbeeld:Een goede ranking zou er een zijn die 98% van de tijd overeenstemt met de uitkomsten van matchups. Een rangorde die slechts 10% van de tijd met de resultaten overeenkomt, zou belabberd zijn - erger dan het opgooien van een munt zonder enige voorkennis.
Een probleem met ranglijsten is dat ze doorgaans discreet zijn, wat betekent dat ze de hele getallen volgen:1, 2, 3, enzovoort. Die volgorde suggereert dat de "afstand" tussen de eerste en tweede gerangschikte leden dezelfde is als die tussen de tweede en derde. Maar dat is niet het geval, zegt Cantwell. De topspelers in een game, wereldwijd, zullen qua vaardigheden dicht bij elkaar liggen, dus het verschil tussen topspelers kan dichterbij zijn dan het lijkt.
"Je ziet vrij vaak dat spelers met een lagere rangorde spelers met een hogere rang kunnen verslaan, en de enige manier waarop het model zinvol kan zijn en de gegevens kan aanpassen, is door alle gelederen samen te persen", zegt Cantwell.
Cantwell en Moore beschreven een systeem dat ranglijsten evalueert op basis van een continu nummeringssysteem. Een rangschikking kan elk reëel getal - geheel getal, breuk, oneindig herhalende decimaal - toewijzen aan een speler in het netwerk. "Continue getallen zijn gemakkelijker om mee te werken", zegt Cantwell, en die continue getallen kunnen nog steeds worden terugvertaald naar discrete rankings.
Bovendien kan deze nieuwe benadering worden gebruikt om iets over de toekomst te voorspellen, zoals de uitkomst van een tennistoernooi, en ook om iets af te leiden over het verleden, zoals hoe een ziekte zich heeft verspreid. "Deze ranglijsten kunnen ons de volgorde van sportteams vertellen van goed naar slecht. Maar ze kunnen ons ook de volgorde vertellen waarin mensen in een gemeenschap besmet raakten met een ziekte", zegt Moore. "Zelfs voor zijn postdoc werkte George aan dit probleem als een manier om het traceren van contacten in een epidemie te verbeteren. Net zoals we kunnen voorspellen welk team een wedstrijd zal winnen, kunnen we afleiden welke van de twee mensen de andere besmette toen ze in contact kwamen met elkaar."
In toekomstig werk zeggen de onderzoekers dat ze van plan zijn om enkele van de diepere vragen die naar voren zijn gekomen te onderzoeken. Meer dan één rangschikking kan het bijvoorbeeld eens zijn met gegevens, maar radicaal oneens met andere rangschikkingen. Of een rangschikking die onjuist lijkt, kan een hoge onzekerheid hebben, maar niet onnauwkeurig zijn. Cantwell zegt dat hij ook de voorspellingen van het model wil vergelijken met de resultaten van echte wedstrijden. Uiteindelijk, zegt hij, kan het model worden gebruikt om voorspellingen te verbeteren in een breed scala van systemen die leiden tot ranglijsten, van infectieziektemodellen tot sportweddenschappen.
Cantwell zegt dat hij zijn geld zal vasthouden - voorlopig. "Ik ben er nog niet helemaal klaar voor om erop te wedden", zegt hij. + Verder verkennen
Kan het 'belief propagation'-algoritme complexe netwerksystemen nauwkeurig beschrijven?
 Onderzoekers ontwikkelen ultrakrachtige plasmonische metaaloxidematerialen
Onderzoekers ontwikkelen ultrakrachtige plasmonische metaaloxidematerialen Studie van zouten in water die opschudding veroorzaken
Studie van zouten in water die opschudding veroorzaken Zeewier, slijm en sokken:de wetenschap achter het zeepsop
Zeewier, slijm en sokken:de wetenschap achter het zeepsop Hoe goede metalen slecht worden:ontdekking verklaart onverwachte eigenschappen van exotische metaalverbindingen
Hoe goede metalen slecht worden:ontdekking verklaart onverwachte eigenschappen van exotische metaalverbindingen Een nieuw systeem om een verbinding te bouwen die cruciaal is voor de ontwikkeling van geneesmiddelen
Een nieuw systeem om een verbinding te bouwen die cruciaal is voor de ontwikkeling van geneesmiddelen
 Meer bewijs dat het weer in Californië naar extremen neigt
Meer bewijs dat het weer in Californië naar extremen neigt Dodental door hittegolf in het noordwesten zal naar verwachting blijven stijgen
Dodental door hittegolf in het noordwesten zal naar verwachting blijven stijgen De Zuidelijke Oceaan neemt het op tegen de hitte van de klimaatverandering
De Zuidelijke Oceaan neemt het op tegen de hitte van de klimaatverandering Vertragen:Nederlanders verlagen maximumsnelheid om vervuiling in te dammen
Vertragen:Nederlanders verlagen maximumsnelheid om vervuiling in te dammen Gedetailleerde consumptieadviezen zouden vrouwen in de VS beter van dienst zijn
Gedetailleerde consumptieadviezen zouden vrouwen in de VS beter van dienst zijn
Hoofdlijnen
- Producten vervaardigd door Anaerobe Ademhaling
- Hoe weet je lichaam het verschil tussen dominante en recessieve genen?
- Kun je later in je leven ambidexter worden? Het hangt er van af
- Bijenschadelijke pesticiden in 75 procent van de honing wereldwijd:studie
- De isovormen van het HP1-eiwit reguleren de organisatie en structuur van heterochromatine
- Hibernerende ribosomen helpen bacteriën te overleven
- De koning van de gewassen kronen:het genoom van de witte Guinea-yam bepalen
- Hoe werken het ademhalingsstelsel en het cardiovasculaire systeem samen?
- Verre verwante virussen delen zelfassemblagemechanisme
 Australië is een wereldwijde top-tien ontbosser - en Queensland loopt voorop
Australië is een wereldwijde top-tien ontbosser - en Queensland loopt voorop Ultradunne gouden nanoribbons met unieke hexagonale kristalfase vertonen vloeistofachtig gedrag
Ultradunne gouden nanoribbons met unieke hexagonale kristalfase vertonen vloeistofachtig gedrag Europa kan gedijen op hernieuwbare energie ondanks onvoorspelbaar weer
Europa kan gedijen op hernieuwbare energie ondanks onvoorspelbaar weer Onderzoekers onthullen elektronica die het menselijk brein nabootst bij efficiënt leren
Onderzoekers onthullen elektronica die het menselijk brein nabootst bij efficiënt leren Chinese privé-satellietdragende raket mislukt na lancering
Chinese privé-satellietdragende raket mislukt na lancering Santos-aandelen stijgen na overnamebod Harbor Energy
Santos-aandelen stijgen na overnamebod Harbor Energy Nieuw helmontwerp kan omgaan met sportieve wendingen
Nieuw helmontwerp kan omgaan met sportieve wendingen Apple onthult nieuwe iPad van $ 299 voor studenten - ondersteunt AR, Apple Potlood
Apple onthult nieuwe iPad van $ 299 voor studenten - ondersteunt AR, Apple Potlood
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com