
Wetenschap
Met een nieuwe techniek kunnen onderzoekers echte systeemkaarten maken op verschillende schalen

Het kunnen bewegen in een netwerk op verschillende schalen is erg belangrijk in systemen waarin je veel op elkaar inwerkende elementen hebt. Krediet:M. Serrano
Onderzoekers van het Institute of Complex Systems van de Universiteit van Barcelona (UBICS) hebben een methode ontwikkeld om netwerksystemen weer te geven, zoals postdiensten en internet, op verschillende schalen, alsof het cartografische kaarten waren.
UBICS-onderzoekers M. Ángeles Serrano, Guillermo García-Pérez en Marian Boguñá, die de studie heeft uitgevoerd die is gepubliceerd in Natuurfysica , een renormalisatiegroepstechniek toegepast op real-world systemen. "Deze techniek stelt ons in staat om een systeem op verschillende resolutieniveaus te verkennen, zoals een soort omgekeerde microscoop waarmee we kunnen uitzoomen en de schaal waarop we de waarneming doen vergroten, " zegt de ICREA-onderzoeksdocent M. Ángeles Serrano, directeur van de studie.
"Het is erg belangrijk om op verschillende schalen door een netwerk te kunnen bewegen in systemen waarin je veel op elkaar inwerkende elementen hebt, zoals de netwerken die we hebben bestudeerd. Deze systemen zijn multiscale netwerken, dat is, hun structuur of bijbehorende processen zijn het resultaat van een mix van structuren en processen op verschillende schalen, " zegt Guillermo García-Pérez, eerste auteur van de studie. "Elke schaal heeft specifieke gegevens, maar schalen zijn ook onderling verbonden, " hij zegt.
De werkelijkheid weergeven als complexe netwerken
De UB-onderzoekers pasten de door hen ontwikkelde techniek toe op bovengenoemde systemen. Hoewel ze verschillend zijn, ze kunnen allemaal worden gedefinieerd in de vorm van knooppunten en verbindingen. In sommige gevallen, bijvoorbeeld in muziek, onderzoekers beschouwen akkoorden als knopen en verbindingen.
In elk geval, al deze systemen kunnen via de "small-world property" worden gedefinieerd als complexe netwerken, omdat de knooppunten in slechts enkele stappen zijn verbonden. "Het is vanwege de kleine wereldeigenschap dat het onmogelijk was geweest om structurele schalen in echt complexe netwerken te splitsen, en om dit te doen, we moesten op elk ervan geometrische kaarten ontwikkelen, zodat we de afstanden tussen knooppunten konden bepalen, ", zegt Marián Boguñá.
Bovendien, deze netwerken vertonen nog twee kenmerken:ze hebben een heterogene connectiviteit, d.w.z., elementen hebben met een hoge connectiviteit en andere met een lage connectiviteit; en ze tonen veel knoopgroeperingen in een driehoekige vorm (clustering).
"Dit is de eerste keer dat een echt geometrische renormalisatiegroep is gedefinieerd in complexe netwerken, " zegt Ángeles Serrano, die eraan toevoegt:"We kunnen nu kaarten maken van complexe netwerken in de meest cartografische zin van het woord, echte kaarten waar elementen of knooppunten posities en afstand tussen hen hebben. Deze kaarten zijn niet alleen aantrekkelijke visuele representaties, maar ze zijn vol betekenis, en ze stellen ons in staat om informatie over de systemen te achterhalen en er doorheen te navigeren. We kunnen de bevaarbaarheid van het systeem vergroten als we rekening houden met de informatie van de renormalisatiegroep, waardoor we netwerken kunnen ontvouwen op de verschillende schalen die ze hebben opgebouwd, en welke, in aanvulling op, blijken op zichzelf te lijken, dat is, ze hebben dezelfde organisatie op verschillende schalen."
Deze resultaten kunnen ook worden toegepast om op kleinere schaal kleinere versies van de oorspronkelijke netwerken te maken met dezelfde eigenschappen. "De mogelijkheid om verkleinde exemplaren te hebben heeft een groot potentieel; ze kunnen dienen als testbank om dure processen in originele netwerken te beoordelen, zoals nieuwe internetrouteringsprotocollen, ’ besluit Serrano.
 Hoe oplosbaarheidsregels vast te stellen
Hoe oplosbaarheidsregels vast te stellen 5de rang Chemieversleuteld activiteit
5de rang Chemieversleuteld activiteit Reiniging van laboratoriumapparatuur
Reiniging van laboratoriumapparatuur Nieuwe robotsensortechnologie kan reproductieve gezondheidsproblemen in realtime diagnosticeren
Nieuwe robotsensortechnologie kan reproductieve gezondheidsproblemen in realtime diagnosticeren Ingenieurs ontwikkelen technologie om specifieke verontreinigingen uit drink- en afvalwater te halen, pijpleidingen
Ingenieurs ontwikkelen technologie om specifieke verontreinigingen uit drink- en afvalwater te halen, pijpleidingen
 Waarom bliksem vaak twee keer inslaat:onderzoek onthult naaldachtige structuren in positief geladen bliksemleiders
Waarom bliksem vaak twee keer inslaat:onderzoek onthult naaldachtige structuren in positief geladen bliksemleiders Koolmonoxide van bosbranden Californië drijft naar het oosten
Koolmonoxide van bosbranden Californië drijft naar het oosten Overstromingen in Delhi terwijl de moessontol in Zuid-Azië oploopt tot bijna 1. 300
Overstromingen in Delhi terwijl de moessontol in Zuid-Azië oploopt tot bijna 1. 300 Positieve menselijke effecten op regenwouden
Positieve menselijke effecten op regenwouden Luchtbeelden geven inzicht in watertrends
Luchtbeelden geven inzicht in watertrends
Hoofdlijnen
- Hoe genoctrooien werken
- Waarom helpen rijmpjes mensen dingen te onthouden?
- Gel elektroforese lezen
- Hernieuwde oproepen voor legale jacht om de groeiende berenpopulatie in Connecticuts onder controle te houden
- Prozac in oceaanwater een mogelijke bedreiging voor het zeeleven, studie vondsten
- Bij voetbalsucces draait alles om vaardigheid:studeren
- Wat is landbouwbiotechnologie?
- Kenmerken van ATP
- Wat is osmotische lyse?
- Wolfraam ontwikkelt lagen onder extreme hitte van fusiereactoren

- Hoe thermische stress te berekenen

- Een materiaal dat continu supergeleidt tot extreme drukken

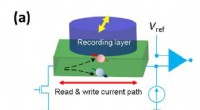
- De weg vrijmaken voor spintronic RAM's:een diepere kijk op een krachtig spinfenomeen
- Onderzoekers creëren blauwdruk voor kwantumbatterij die geen lading verliest

 Ruimteagentschappen onthullen site met veranderingen in de afsluiting van de aarde
Ruimteagentschappen onthullen site met veranderingen in de afsluiting van de aarde Hoe online buurtbeoordelingen stadsplanning kunnen helpen
Hoe online buurtbeoordelingen stadsplanning kunnen helpen Waarom piepen eekhoorns in bomen?
Waarom piepen eekhoorns in bomen?  China wint oorlog tegen smog, levensverwachting helpen:studeren
China wint oorlog tegen smog, levensverwachting helpen:studeren Methaan uitgestoten door mensen enorm onderschat, onderzoekers vinden
Methaan uitgestoten door mensen enorm onderschat, onderzoekers vinden Hoe bijen hun weg naar huis vinden
Hoe bijen hun weg naar huis vinden Zilveren nanodeeltjes vangen kwik op
Zilveren nanodeeltjes vangen kwik op PolyU ontwikkelt nieuwe efficiënte en goedkope semi-transparante perovskiet-zonnecellen met grafeenelektroden
PolyU ontwikkelt nieuwe efficiënte en goedkope semi-transparante perovskiet-zonnecellen met grafeenelektroden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

