
Wetenschap
Natuurlijke systemen vertonen niet-lokale correlaties
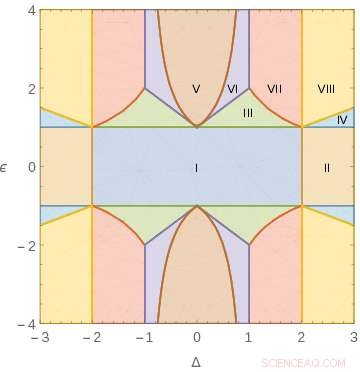
Parametergebieden met verschillend gedrag van de klassieke grens voor een XXZ-achtige Hamiltoniaan met twee parameters. Krediet:ICFO
Klassieke correlaties maken deel uit van ons dagelijks leven. Bijvoorbeeld, als men altijd een paar sokken van dezelfde kleur en vorm aantrekt, kijken naar de kleur of vorm van een sok bepaalt de kleur of vorm van het paar. Nog meer, door de kleur en vorm van de ene sok te observeren en tegelijkertijd de kleur en vorm van de andere te kennen.
In het kwantumrijk, Het onzekerheidsprincipe van Heisenberg stelt dat het nauwkeurig meten van een paar eigenschappen van een atoom een limiet stelt aan de meetnauwkeurigheid die je kunt verkrijgen voor dezelfde eigenschappen van een ander atoom. Daarom, als men zegt dat de sokken verstrikt zijn, het observeren van de kleur van de ene sok zou ons in staat stellen de kleur van de andere te voorspellen. Echter, als we ook kijken naar de vorm van de sok, dit zou de kleur "verstoren", waardoor het tot op zekere hoogte volkomen onvoorspelbaar is. Deze vreemde "synchronisatie" tussen deeltjes wordt gedefinieerd als kwantumverstrengeling, en is een van de intrinsieke kenmerken van de kwantumwereld.
In de natuur, er bestaat een veel vreemdere vorm van zogenaamde niet-lokale correlaties, die zich manifesteren door enkele verstrengelde toestanden tussen atomaire deeltjes. Door de minimale aannames te maken dat eigenschappen van objecten (vorm/kleur) bestaan, ongeacht onze kennis ervan, en die informatie kan niet onmiddellijk worden verspreid, men vindt dat de kwantumfysica correlaties kan genereren die onverenigbaar zijn met deze twee schijnbaar redelijke principes.
Hoewel buitengewoon fascinerend om te bestuderen, deze niet-lokale correlaties zijn om drie redenen erg moeilijk te karakteriseren in systemen die uit veel deeltjes bestaan. Eerst, klassieke correlaties zijn wiskundig zeer complex om te bestuderen; tweede, quantum veel-lichaamstoestanden zijn erg complex om te beschrijven vanwege de exponentiële groei van hun beschreven toestanden; en, derde, momenteel beschikbare experimentele technieken zijn vrij beperkt, beperking van de metingen die in het laboratorium kunnen worden uitgevoerd. Om de rol van niet-lokale correlaties in kwantumsystemen met veel lichamen te onderzoeken, men moet dus deze drie problemen tegelijkertijd aanpakken.
In een recent artikel gepubliceerd in Fysieke beoordeling X , een team van wetenschappers van MPQ in München, ICFO in Barcelona, De Universiteit van Innsbruck en het Centrum voor Theoretische Fysica van de Poolse Academie van Wetenschappen hebben een eenvoudige test voorgesteld om niet-lokale correlaties in kwantum veeldeeltjessystemen te bestuderen. Ze hebben onderzocht of niet-lokale correlaties in natuurlijke systemen voorkomen als grondtoestanden van sommige spin-Hamiltonianen, zoals elektronen (beschreven door hun spin-vrijheidsgraad) in een systeem van één ruimtelijke dimensie. Door numerieke en analytische resultaten te combineren, ze hebben aangetoond dat sommige Hamiltonianen die al tientallen jaren door natuurkundigen zijn bestudeerd, een toestand van minimale energie hebben die niet-lokale correlaties kan vertonen.
Als eerste auteur, Jordi Tura, heeft commentaar gegeven, "We bieden een set tools om een probleem te bestuderen dat op zichzelf altijd al ingewikkeld was. De technieken die we hebben ontwikkeld zijn veel eenvoudiger dan de vorige. Als je ze in het laboratorium wilde implementeren, je zou er alleen voor moeten zorgen dat het systeem wordt voorbereid in een staat van voldoende lage energie."
De resultaten werpen enig licht op dit fascinerende probleem, hopelijk tot verdere vooruitgang in ons begrip van niet-lokaliteit in quantum veel-lichamensystemen.
 De beweging van fluorescerende sondes door het celmembraan stimuleren
De beweging van fluorescerende sondes door het celmembraan stimuleren Gecombineerde röntgen- en fluorescentiemicroscoop onthult onzichtbare moleculaire details
Gecombineerde röntgen- en fluorescentiemicroscoop onthult onzichtbare moleculaire details Video:Kameleons zijn meesters in nanotechnologie
Video:Kameleons zijn meesters in nanotechnologie Het verschil tussen atomen, ionen, moleculen en verbindingen
Het verschil tussen atomen, ionen, moleculen en verbindingen  Schimmelwegen op kaaskorst beïnvloeden voedselveiligheid, rijpheid
Schimmelwegen op kaaskorst beïnvloeden voedselveiligheid, rijpheid
 Weersomstandigheden na een koud front
Weersomstandigheden na een koud front De vroegste menselijke invloed op geologische processen vond plaats 11, 500 jaar geleden (update)
De vroegste menselijke invloed op geologische processen vond plaats 11, 500 jaar geleden (update) Yellowstone rammelde door zwerm van meer dan 140 aardbevingen in de afgelopen dag, geologen zeggen:
Yellowstone rammelde door zwerm van meer dan 140 aardbevingen in de afgelopen dag, geologen zeggen: Werkt natuurlijke selectie op Genotype of Phenotype?
Werkt natuurlijke selectie op Genotype of Phenotype?  Klimaatwetenschappers ontdekken 30 jaar oud temperatuurrecord
Klimaatwetenschappers ontdekken 30 jaar oud temperatuurrecord
Hoofdlijnen
- Hoe regenereert de huid?
- Sarcodina Life Cycle
- Een geïntegreerde beoordeling van vaatplantensoorten in Amerika
- Wat is de rol van het IgM-antilichaam?
- Hoe wordt glucose opgeslagen in plantencellen?
- 2 kiwivogels zijn zeldzaam lichtpuntje in grimmig uitstervingsrapport
- Wat is de vloeistof die de ruimte tussen de kern en het celmembraan vult?
- Controversiële onkruidverdelger houdt EU in de knoop (Update)
- Alles-in-één reparatiekit maakt CRISPR-genbewerking nauwkeuriger
- Snelheid plus controle in nieuwe computerchip - het vertragen van licht naar geluid

- IceCube-detectie van een hoogenergetisch deeltje bewijst 60 jaar oude theorie

- Laserstralen van antimaterie tot bestaan

- Geconstrueerde meta-oppervlakken vervangen plakband in gespecialiseerde microscoop

- Corrosie kan de duurzaamheid van materialen verbeteren

 Hoe de nucleaire wapenwedloop werkt
Hoe de nucleaire wapenwedloop werkt  Offshore olie- en gasplatforms stoten meer methaan uit dan eerder geschat
Offshore olie- en gasplatforms stoten meer methaan uit dan eerder geschat Filippijnse vulkaanuitbarsting kan volgende winter leiden tot opwarming van El Nino
Filippijnse vulkaanuitbarsting kan volgende winter leiden tot opwarming van El Nino Honderden kandidaat-sterrenstelsels geïdentificeerd in de protocluster D1UD01
Honderden kandidaat-sterrenstelsels geïdentificeerd in de protocluster D1UD01 Insecten die op bedwantsen lijken
Insecten die op bedwantsen lijken  Hoe maak je continue rollen grafeen?
Hoe maak je continue rollen grafeen? Vulkanische uitbarstingen, orkanen beïnvloeden de regenval op het eiland Hawaï
Vulkanische uitbarstingen, orkanen beïnvloeden de regenval op het eiland Hawaï Native Plants & Animals of China
Native Plants & Animals of China
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

