
Wetenschap
Als een voetballer schopt zodat het 3 seconden in de lucht doorbrengt en 50 m reist, vind dan de snelheidshoek van de kick?
Inzicht in de fysica
* Projectielbeweging: Het traject van het voetbal is een klassiek voorbeeld van projectielbeweging, waarbij de enige kracht die erop werkt, de zwaartekracht is na de eerste kick.
* Horizontale en verticale componenten: We moeten rekening houden met de horizontale (x) en verticale (y) componenten van de snelheid van het voetbal.
* vluchttijd: De tijd die de bal in de lucht doorbrengt, is gerelateerd aan de verticale snelheid.
* Bereik: De horizontale afgelegde afstand (50 m) is gerelateerd aan de horizontale snelheid en het tijdstip van de vlucht.
oplossing
1. Verticale beweging:
* We weten dat de tijd van vlucht (t) 3 seconden is.
* De versnelling als gevolg van zwaartekracht (g) is -9,8 m/s².
* De vergelijking gebruiken:
* t =2 * (v_y / g) (waarbij v_y de initiële verticale snelheid is)
* We kunnen oplossen voor v_y:
* v_y =(g * t) / 2 =(-9,8 m / s² * 3 s) / 2 =-14.7 m / s
* Het negatieve teken geeft aan dat de initiële verticale snelheid omhoog is.
2. Horizontale beweging:
* De horizontale snelheid (v_x) blijft constant gedurende de vlucht.
* We kunnen het bereik (r) en de tijd (t) gebruiken om v_x te vinden:
* R =v_x * t
* v_x =r / t =50 m / 3 s =16,67 m / s
3. schophoek (θ):
* De hoek van de kick (θ) is gerelateerd aan de horizontale en verticale componenten van snelheid:
* tan (θ) =v_y / v_x
* θ =arctan (v_y / v_x) =arctan (-14.7 m / s / 16.67 m / s) ≈ -41,8 °
Belangrijke opmerking: De hoek is negatief omdat de initiële verticale snelheid omhoog is. Om de hoek uit te drukken ten opzichte van de horizontale, nemen we de absolute waarde aan:
Daarom is de hoek van de trap ongeveer 41,8 ° boven de horizontale.
 Hoe beïnvloeden planten de landvorm van de aarde?
Hoe beïnvloeden planten de landvorm van de aarde?  Wereld kan te maken krijgen met voedselcrisis in de nasleep van coronavirus:VN, WTO
Wereld kan te maken krijgen met voedselcrisis in de nasleep van coronavirus:VN, WTO Navigeren in de transitie naar schone energie tijdens de COVID-19-crisis
Navigeren in de transitie naar schone energie tijdens de COVID-19-crisis NASA-NOAA-satelliet die Barry volgt door Louisiana, Arkansas
NASA-NOAA-satelliet die Barry volgt door Louisiana, Arkansas Tropische regenwouden voor kinderen
Tropische regenwouden voor kinderen
Hoofdlijnen
- Waar komt de Fox Glove Plant vandaan?
- Welke organen in uw buik zijn solide?
- Wat is het doel van de promotor en terminatorregio van de DNA-molecule?
- Vogelgriep bij rundvee:wat zijn de zorgen rond het nieuw opkomende runder-H5N1-griepvirus?
- Wat is de route genomen door zuurstofdeeltjes wanneer ze in de mond gaan en naar cellen reizen?
- Onderzoekers genereren tomaten met verbeterde antioxiderende eigenschappen door genetische manipulatie
- Bacteriën in de dikke darm zijn belangrijk omdat ze belangrijk synthetiseren?
- Kunnen milieutoxines de biologische klok verstoren?
- Is dat een teelbal of een iriserende streep? De mannelijke ware kleuren van een vrouwelijke inktvis
- Natuurkundigen met groene vingers schatten de boomspanningssnelheid in willekeurige netwerken
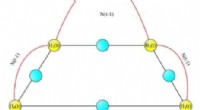
- Onderzoekers observeren dwarse wiebelbanden in neodymium-136
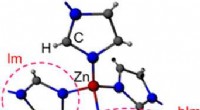
- Metaal-organische verbindingen produceren nieuwe glasklasse
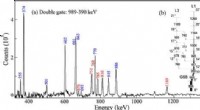
- Massieve deeltjes testen standaard kwantumtheorie

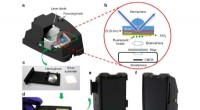
- Plasmonics verbetert de gevoeligheid van smartphonemicroscopie
 Wat kwam eerst Mercurius de planeet of het element?
Wat kwam eerst Mercurius de planeet of het element?  Gebruik de periodiek systeem om de molaire massa KL en CACL2 te berekenen?
Gebruik de periodiek systeem om de molaire massa KL en CACL2 te berekenen?  Oude parasieten laten zien dat reinheid mogelijk naast ziekte heeft gestaan
Oude parasieten laten zien dat reinheid mogelijk naast ziekte heeft gestaan  5 Aardse feiten om de geest van uw kind te verbazen
5 Aardse feiten om de geest van uw kind te verbazen  Van blingbling tot hypercars, grenzeloze luxe te zien in Genève
Van blingbling tot hypercars, grenzeloze luxe te zien in Genève Wat is de fysische toestand bij kamertemperatuur van waterstofsulfide?
Wat is de fysische toestand bij kamertemperatuur van waterstofsulfide?  Maakt de zwaartekracht objecten in de ruimte buigen?
Maakt de zwaartekracht objecten in de ruimte buigen?  Is een samengestelde lichtmicroscoop nodig om biologie op chemisch niveau te bestuderen?
Is een samengestelde lichtmicroscoop nodig om biologie op chemisch niveau te bestuderen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

