
Wetenschap
Van welke vereiste moet worden voldaan door een kracht die op deeltje werkt om eenvoudige harmonische beweging te ondergaan?
Wiskundig kan dit worden uitgedrukt als:
f =-kx
waar:
* f is de kracht die op het deeltje werkt
* x is de verplaatsing van het deeltje vanuit zijn evenwichtspositie
* K is een positieve constante genaamd de veerconstante (of stijfheid)
Deze vergelijking vertegenwoordigt de wet van Hooke, die de herstelkracht van een ideale veer beschrijft.
Dit is de reden waarom deze voorwaarde leidt tot eenvoudige harmonische beweging:
* Herstel Force: De kracht werkt altijd om het deeltje terug te trekken naar zijn evenwichtspositie, vandaar het negatieve teken.
* Lineaire relatie: De kracht is recht evenredig met de verplaatsing, wat betekent dat een grotere verplaatsing resulteert in een sterkere herstelkracht.
* oscillerende beweging: Deze combinatie van een herstelkracht en een lineaire relatie leidt tot oscillaties. Het deeltje versnelt naar evenwicht, overschrijdt en versnelt vervolgens weer terug, waardoor een repetitieve, sinusvormige beweging ontstaat.
Voorbeelden van systemen die eenvoudige harmonische beweging vertonen:
* Een massa bevestigd aan een veer
* Een slinger slingert met een kleine amplitude
* Een trillende afstemmingsvork
Belangrijke opmerking: Hoewel de kracht evenredig moet zijn met de verplaatsing, is het belangrijk om te onthouden dat de beweging * niet * noodzakelijkerwijs lineair is. Een slinger ondergaat bijvoorbeeld SHM in een boog, geen rechte lijn. De * herstelkracht * werkt echter altijd langs de lijn die de slinger Bob verbindt met zijn evenwichtspositie.
 Wordt een enzym in een reactie geconsumeerd?
Wordt een enzym in een reactie geconsumeerd?  Wat is de dichtheid in G L van chloorgas bij 7,50 102 Torr en 25,0ºC molmassa is gelijk aan 70,9 mol?
Wat is de dichtheid in G L van chloorgas bij 7,50 102 Torr en 25,0ºC molmassa is gelijk aan 70,9 mol?  Hoe noem je een ander metaal dan ijzer en legeringen?
Hoe noem je een ander metaal dan ijzer en legeringen?  De stabiliteit van een nuclide hangt af van de?
De stabiliteit van een nuclide hangt af van de?  Een enzym dat het beste werkt in een zure omgeving zou werken met een pH van wat?
Een enzym dat het beste werkt in een zure omgeving zou werken met een pH van wat?
 Wat zijn de drie landvormregio's van de Midden-Atlantische staten?
Wat zijn de drie landvormregio's van de Midden-Atlantische staten?  Aardbeving met een kracht van 6,7 op de schaal van Richter treft Filipijnen:USGS
Aardbeving met een kracht van 6,7 op de schaal van Richter treft Filipijnen:USGS Scheepssporen laten zien hoe aerosols wolken snel en langzaam beïnvloeden
Scheepssporen laten zien hoe aerosols wolken snel en langzaam beïnvloeden Studie impliceert verder dat pluimveeverwerking betrokken is bij kustvervuiling
Studie impliceert verder dat pluimveeverwerking betrokken is bij kustvervuiling Vermengen de Atlantische en Stille Oceaan zich?
Vermengen de Atlantische en Stille Oceaan zich?
Hoofdlijnen
- Hoe gekoppelde gegevens en kunstmatige intelligentie dieren kunnen helpen
- Sommige prokaryotische en eukaryotische cellen hebben een cellulaire structuur genaamd flagella. Wat is het doel van flagella?
- Welke stap is niet bereikt door wetenschappers die de oorsprong van het leven bestuderen?
- Wat zijn natuurlijke meststoffen en wat hun bronnen?
- Wat is de wetenschappelijke classificatie van Maple Tree Kingdoms?
- Signaalmolecuul kan eiwitten in tarweplanten reguleren
- Proces door welke evolutie optreedt?
- Wat zijn de fysieke eigenschappen van de Griekse God?
- Welke organel wordt in de meeste plantencellen gevonden maar nooit dierlijke cellen?
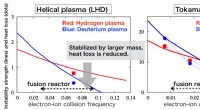
- Verduidelijking van het mechanisme voor het onderdrukken van turbulentie door ionenmassa
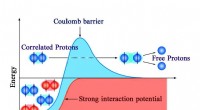
- Wetenschappers presenteren nieuwe metingen van β-vertraagd twee-protonverval van 27S
- Kwantummagneten in beweging

- Skyrmion-wervelingen zijn veelbelovend voor energiezuinige computercircuits

- Discovery biedt nieuwe mogelijkheden voor gegevensopslag van de volgende generatie

 Hoeveel druk kan ijzer weerstaan?
Hoeveel druk kan ijzer weerstaan?  Waarom reproduceren sommige organismen zich aseksueel?
Waarom reproduceren sommige organismen zich aseksueel?  Waar stort een ster in als zijn elementen sterft?
Waar stort een ster in als zijn elementen sterft?  Wetenschappers kweken optische chips in petrischaal
Wetenschappers kweken optische chips in petrischaal Natuurkundigen ontdekken nieuw dynamisch raamwerk voor turbulentie
Natuurkundigen ontdekken nieuw dynamisch raamwerk voor turbulentie Wat zijn de twee edelstenen genoemd als Augusts Birth Stone?
Wat zijn de twee edelstenen genoemd als Augusts Birth Stone?  Hoe verschilt de biologische evolutie van chemische evolutie?
Hoe verschilt de biologische evolutie van chemische evolutie?  Koolstof nanobuisjes bootsen biologie na
Koolstof nanobuisjes bootsen biologie na
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

