
Wetenschap
Een bal wordt uit de grond in de lucht gegooid op een hoogte van 9,1 m snelheid waargenomen als V7.6i 6.1J in meters per seconde X -as horizontaal y verticaal en hoger dan wat maximale h?
Inzicht in het probleem
* Initiële voorwaarden: We weten dat de bal begint op een hoogte van 9,1 meter en een beginsnelheid van (7,6i + 6.1j) m/s heeft.
* doel: We moeten de maximale hoogte vinden die de bal bereikt.
fysica -concepten
* Projectielbeweging: De bal ondergaat projectielbeweging, wat betekent dat de beweging ervan kan worden geanalyseerd in de horizontale (x) en verticale (y) richtingen afzonderlijk.
* Verticale beweging: De verticale beweging wordt beïnvloed door de zwaartekracht, waardoor de bal vertraagt terwijl deze omhoog gaat en vervolgens wordt versneld als deze weer naar beneden valt.
* Maximale hoogte: Op de maximale hoogte is de verticale snelheid van de bal nul.
oplossing
1. Verticale snelheidscomponent: De initiële verticale snelheid is de Y-component van de initiële snelheidsvector:V_iy =6,1 m/s.
2. versnelling als gevolg van de zwaartekracht: De versnelling als gevolg van de zwaartekracht werkt naar beneden:a_y =-9,8 m/s².
3. Verticale bewegingsvergelijking: We kunnen de volgende kinematische vergelijking gebruiken om de maximale hoogte (h) te vinden:
v_fy² =v_iy² + 2a_y (h - h_i)
* v_fy =laatste verticale snelheid (0 m/s op de maximale hoogte)
* v_iy =initiële verticale snelheid (6,1 m/s)
* a_y =versnelling als gevolg van zwaartekracht (-9,8 m/s²)
* h =maximale hoogte (wat we willen vinden)
* h_i =initiële hoogte (9,1 m)
4. Oplossen voor H:
0² =6.1² + 2 (-9.8) (h - 9.1)
37.21 =19.6 (h - 9.1)
H - 9.1 =1.9
h =11 m
Antwoord
De maximale hoogte bereikt door de bal is 11 meter .
 Vraag en antwoord:La Nina kan meer Atlantische stormen brengen, westelijke droogte
Vraag en antwoord:La Nina kan meer Atlantische stormen brengen, westelijke droogte Stedelijke overstromingen intensiveren, platteland droogt op
Stedelijke overstromingen intensiveren, platteland droogt op Atmosferische salpeterigzuurchemie onthult een aanzienlijk onderschatte oxidatiecapaciteit in Noord-China
Atmosferische salpeterigzuurchemie onthult een aanzienlijk onderschatte oxidatiecapaciteit in Noord-China Hoe begripvol in het ecosysteem komt mensen ten goede?
Hoe begripvol in het ecosysteem komt mensen ten goede?  30 jaar geleden gewaarschuwd, opwarming van de aarde is in onze woonkamer
30 jaar geleden gewaarschuwd, opwarming van de aarde is in onze woonkamer
Hoofdlijnen
- Wat zou er gebeuren met celreproductie als THR Nucleus van A niet aanwezig was?
- Waarom hebben alle cellen mitochondriën nodig?
- Hoe maak je een Paper Mache Cell
- Symbiose en celevolutie:Lynn Margulis en de oorsprong van eukaryoten
- Wat bedoel je met fysiologische waarde?
- Welke organel is het controlecentrum van de cel waarom?
- Waarom eten we in Science Lab?
- Wat betekent het om een hybride te zijn voor eigenschap die onvolledig dominant is?
- Waar kom je in het dagelijks leven stikstof tegen, zowel in de vorm van een verbinding als van een mengsel?
- Onderzoekers behalen kwantumvoordeel

- Hoe coronavirus-aerosolen door de longen reizen

- Uit onderzoek blijkt dat de fijne structuurconstante van kwantumspin-ijs groot is

- In-situ diagnose van femtoseconde lasersondepulsen voor ultrasnelle beeldvormingstoepassingen
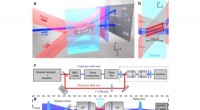
- Monolaag overgangsmetaal dichalcogenide lens voor beeldvorming met hoge resolutie

 Koolstofafvangproces produceert waterstof en bouwmaterialen
Koolstofafvangproces produceert waterstof en bouwmaterialen Optische technieken onderzoeken giftige stoffen in cellen
Optische technieken onderzoeken giftige stoffen in cellen Mahathir werpt theorie van overname op afstand op in MH370-mysterie
Mahathir werpt theorie van overname op afstand op in MH370-mysterie Wat is de golflengte van een 30 GHz radiogolf in vacuüm?
Wat is de golflengte van een 30 GHz radiogolf in vacuüm?  Is HCI een samengesteld mengsel of element?
Is HCI een samengesteld mengsel of element?  Love Island:de psychologische uitdagingen waarmee deelnemers en kijkers kunnen worden geconfronteerd nadat de show voorbij is
Love Island:de psychologische uitdagingen waarmee deelnemers en kijkers kunnen worden geconfronteerd nadat de show voorbij is Kan een mengsel van zout en water oplossing worden genoemd (uitleggen)?
Kan een mengsel van zout en water oplossing worden genoemd (uitleggen)?  Fans verheugen zich:streaming zonder abonnement voor NFL-games
Fans verheugen zich:streaming zonder abonnement voor NFL-games
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

