
Wetenschap
Is een beweging van handen klok eenvoudige harmonische beweging?
* SHM vereist een herstelkracht die evenredig is aan verplaatsing: In SHM is de kracht die een object terugbrengt naar zijn evenwichtspositie recht evenredig met de verplaatsing van het object vanuit die positie. Dit betekent dat de kracht sterker wordt naarmate de verplaatsing groter wordt. De handen van een klok ervaren geen kracht als deze.
* Klokken beweegt met een constante hoeksnelheid: De handen van een klok bewegen met een constante snelheid, wat betekent dat ze dezelfde hoek in dezelfde hoeveelheid tijd bestrijken. Dit is niet kenmerkend voor SHM, waarbij de snelheid in de loop van de tijd verandert.
* shm is periodiek en sinusoïdaal: SHM wordt beschreven door een sinusvormige functie (zoals sinus of cosinus). De beweging van klokken is periodiek maar niet sinusoïdaal. Ze bewegen met een constante snelheid op een cirkelvormig pad.
Analogie: Denk aan een slinger. Een slinger zwaait heen en weer en de beweging ervan kan worden benaderd als SHM omdat de herstelkracht (zwaartekracht) evenredig is met de verplaatsing van de verticaal. Een klokhand gedraagt zich niet zo.
Samenvattend: Hoewel de beweging van klokken periodiek is, mist het de belangrijkste kenmerken van eenvoudige harmonische beweging:een herstelkracht die evenredig is aan verplaatsing, een variërende snelheid en een sinusvormig pad.
 Een dagelijkse verstoring vanuit de bovenste atmosfeer laat zijn sporen na op tropische regenval
Een dagelijkse verstoring vanuit de bovenste atmosfeer laat zijn sporen na op tropische regenval Wat beschrijft het landwater en de lucht op aarde die het leven in stand houdt?
Wat beschrijft het landwater en de lucht op aarde die het leven in stand houdt?  Een nieuwe aanpak voor droogtemonitoring
Een nieuwe aanpak voor droogtemonitoring G7 wil kolencentrales tegen midden 2030 uitfaseren
G7 wil kolencentrales tegen midden 2030 uitfaseren  Hoge kooldioxide kan krimpende stengels in moerassen creëren
Hoge kooldioxide kan krimpende stengels in moerassen creëren
Hoofdlijnen
- Komen uitgestorven virussen terug dankzij klimaatverandering?
- De Nepalese natuur wordt bedreigd door nieuwe ontwikkelingsdrang:natuurbeschermers
- Waarom kunnen prokaryotische cellen kleiner zijn dan eukaryotisch en nog steeds alle functies van het leven voortzetten?
- Wat is cyberchondrie?
- Hoe de hersenen geuren buitensluiten
- Wat is een uitdrukking van de wet (kconstante)?
- Wat is de complementaire standaard voor dit DNA -molecuul G a T C C?
- Wat is de eerste soort in secundaire opvolging?
- Welke twee factoren beïnvloeden rechtstreeks de eigenschappen van een organisme?
- Kwantumvreemdheid leidt tot nieuwe elektronica

- Kunstmatige intelligentie versnelt voorspellingen om fusie-experimenten te controleren

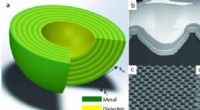
- Nano-imprinted hyperlens-array:de weg vrijmaken voor praktische beeldvorming met superresolutie
- Nieuwe ontdekking over terahertz-straling komt ten goede aan de biogeneeskunde

- Floppy atomaire dynamica helpt warmte om te zetten in elektriciteit

 Hoe eencellige organismen en meercellige uitwisselingsmaterialen?
Hoe eencellige organismen en meercellige uitwisselingsmaterialen?  Wat zijn de 7 kenmerken die kunnen worden gebruikt om mineralen te beschrijven?
Wat zijn de 7 kenmerken die kunnen worden gebruikt om mineralen te beschrijven?  De snelheid waarmee snelheid verandert?
De snelheid waarmee snelheid verandert?  Wat gebeurt er met de warmte -energie die vast wordt geleverd zodra deze is begonnen met smelten?
Wat gebeurt er met de warmte -energie die vast wordt geleverd zodra deze is begonnen met smelten?  Welke mineralen en gesteenten worden in Turkije gevonden?
Welke mineralen en gesteenten worden in Turkije gevonden?  Onderzoeker stelt dat de groei van vriendjespolitiek de Amerikaanse welvaart bedreigt
Onderzoeker stelt dat de groei van vriendjespolitiek de Amerikaanse welvaart bedreigt Hoe worden micro -organismen gebruikt in alcohol?
Hoe worden micro -organismen gebruikt in alcohol?  Welke deze elementen lijken volgens de periodieke wet het meest op elkaar:natriumfosfor en zwavel?
Welke deze elementen lijken volgens de periodieke wet het meest op elkaar:natriumfosfor en zwavel?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

