
Wetenschap
Wat zijn de voorbeelden van dimensieloze hoeveelheden in de natuurkunde?
Veelgebruikte dimensieloze hoeveelheden:
* hoek: Gemeten in radialen of graden, is hoek een dimensieloze verhouding tussen booglengte tot straal.
* stam: Beschrijft de vervorming van een materiaal onder stress. Het is de verhouding van verandering in lengte tot oorspronkelijke lengte, waardoor het dimensieloos is.
* de verhouding van Poisson: Vertegenwoordigt de verhouding van transversale spanning tot axiale spanning in een materiaal. Het is een maat voor hoeveel een materiaal vervormt in richtingen loodrecht op de toegepaste spanning.
* Relatieve vochtigheid: De verhouding van de gedeeltelijke druk van waterdamp in de lucht tot de verzadigingsdampdruk bij een gegeven temperatuur.
* Specifiek gewicht: De verhouding van de dichtheid van een substantie tot de dichtheid van een referentie -substantie (meestal water).
* Mach -nummer: De verhouding van de snelheid van een object tot de snelheid van het geluid in het omliggende medium.
* Reynolds -nummer: Een dimensieloze hoeveelheid die wordt gebruikt in vloeistofmechanica om stroompatronen te voorspellen. Het is de verhouding tussen traagheid tot viskeuze krachten.
Andere voorbeelden:
* Efficiëntie: De verhouding van nuttig uitgangsvermogen tot invoervermogen.
* Restitutiecoëfficiënt: Een maat voor de "veerkracht" van een botsing, die de verhouding van relatieve snelheid na de botsing tot relatieve snelheid voor de botsing vertegenwoordigt.
* Wrijvingsfactor: Gebruikt in vloeistofmechanica om de weerstand tegen stroming in pijpen en andere leidingen te beschrijven.
* Fasehoek: In oscillaties en golven beschrijft de fasehoek de relatieve positie van twee oscillaties of golven. Het is het verschil in hun fasen, gemeten in radialen of graden.
* Quantumnummers: Gebruikt om de eigenschappen van atomaire en subatomaire deeltjes te beschrijven, zijn sommige kwantumnummers (zoals het belangrijkste kwantumnummer) dimensieloos.
Waarom zijn dimensieloze hoeveelheden belangrijk?
* Universaliteit: Dimensieloze hoeveelheden vertegenwoordigen vaak fundamentele relaties die waar zijn op verschillende schalen en eenheden.
* vereenvoudiging: Door de invloed van eenheden te verwijderen, vereenvoudigen ze vergelijkingen en maken het gemakkelijker om resultaten van verschillende systemen te vergelijken.
* Gegevensanalyse: Ze helpen gegevens te normaliseren en maken het gemakkelijker om trends te analyseren.
* Modellering: Ze zijn cruciaal in het ontwikkelen van theoretische modellen en simulaties, omdat ze mogelijk maken dat relaties in een algemene vorm worden uitgedrukt.
Voorbeelden in vergelijkingen:
* sin (θ): De sinusfunctie neemt een hoek (θ) als invoer en de uitgang is een dimensieloos nummer.
* e^( - kt): De exponentiële functie, vaak gebruikt in vervalprocessen, omvat de exponentiële constante 'E' en een dimensieloze combinatie van een snelheidsconstante 'k' en tijd 't'.
Voel je vrij om te vragen of je meer voorbeelden of verdere uitleg van een van deze concepten wilt!
 Onderzoekers reproduceren Great Wave-schilderij op microschaal met inktloze technologie
Onderzoekers reproduceren Great Wave-schilderij op microschaal met inktloze technologie Interdisciplinair team ontwerpt gasstroomcel om katalytisch gedrag te analyseren
Interdisciplinair team ontwerpt gasstroomcel om katalytisch gedrag te analyseren Is benzoëzuur sterker dan HCl?
Is benzoëzuur sterker dan HCl?  Is Bismuth een metaal of niet-metaal?
Is Bismuth een metaal of niet-metaal?  Hoeveel mol N2 worden geproduceerd door de ontleding 2.88 mol natriumazide?
Hoeveel mol N2 worden geproduceerd door de ontleding 2.88 mol natriumazide?
 Redactioneel:De wereld had een klap nodig van de klimaatbijeenkomst in Madrid. Het kreeg in plaats daarvan een gejammer
Redactioneel:De wereld had een klap nodig van de klimaatbijeenkomst in Madrid. Het kreeg in plaats daarvan een gejammer Draagt uw koffie bij aan het malariarisico?
Draagt uw koffie bij aan het malariarisico? Kan vervuiling uit natuurlijke bronnen komen?
Kan vervuiling uit natuurlijke bronnen komen?  Trump wil schoon energieplan Obama terugdraaien
Trump wil schoon energieplan Obama terugdraaien Onderzoekers modelleren de verspreiding van boomsoorten in het Amazonegebied
Onderzoekers modelleren de verspreiding van boomsoorten in het Amazonegebied
Hoofdlijnen
- Wat is het trofische niveau van gordeldieren?
- Wat heeft een cel?
- Hoe de cholerabacterie waterroofdieren overleeft
- Hoe vergelijk ik Frankenstein & Cloning?
- Wetenschappers laten zien hoe eiwitten de evolutionaire inzet verslaan
- Hoe worden de eigenschappen niet gemanifesteerd bij ouders die nakomelingen verschijnen?
- Welke twee stoffen heeft een foetus nodig om volledig potentieel te groeien?
- DNA -transcriptie is de productie van?
- Wat is de acetabulofemoral?
- Wetenschappers kapen open access kwantumcomputer om kwantumgeheimen te ontrafelen

- Het steen-papier-schaar-spel en samenleven

- Atomaire imperfecties brengen het kwantumcommunicatienetwerk dichter bij de realiteit
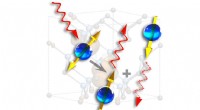
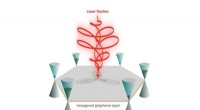
- Graphene valleytronics:de weg vrijmaken voor kleine kwantumcomputers op kamertemperatuur
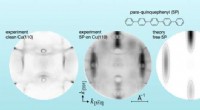
- Natuurkundigen ontdekken nieuwe regel voor orbitaalvorming bij chemische reacties
 Is de Mid Ocean Ridge -locatie van de oudste verdieping?
Is de Mid Ocean Ridge -locatie van de oudste verdieping?  Mechanica, chemie en biomedisch onderzoek bundelen krachten voor niet-invasieve weefseltherapie
Mechanica, chemie en biomedisch onderzoek bundelen krachten voor niet-invasieve weefseltherapie Wat is sterker azijnzuur of ethanol?
Wat is sterker azijnzuur of ethanol?  Nieuwe aanpak kan snel de beste organische zonnecelmengsels identificeren
Nieuwe aanpak kan snel de beste organische zonnecelmengsels identificeren Wat zijn enkele voorbeelden van eiwitten?
Wat zijn enkele voorbeelden van eiwitten?  Wat zijn de vijf landen in een gematigde zone?
Wat zijn de vijf landen in een gematigde zone?  Welke is de oervevel?
Welke is de oervevel?  Wat is de grootste de Sun Moon of de aarde?
Wat is de grootste de Sun Moon of de aarde?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

